32 bài tập Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn (có lời giải)

Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được x mét vải lụa (1 ≤ x ≤ 18). Tổng chi phí sản xuất x mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí: C (x) = x³ – 3x² – 20x + 500.

Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 220 nghìn đồng/mét. Gọi B (x) là số tiền bán được và L (x) là lợi nhuận thu được khi bán x mét vải lụa.

a) Hãy viết biểu thức tính B (x) và L (x) theo x.

b) Khảo sát và vẽ đồ thị của hàm số L (x) trên [1; 18].

c) Hộ làm nghề dệt này cần sản xuất và bán ra mỗi ngày bao nhiêu mét vải lụa để thu được lợi nhuận tối đa? Tính lợi nhuận tối đa đó.

Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f  > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d ′ là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d ′ > 0, ảnh ảo thì d ′ < 0). Ta có công thức: \[\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}{\rm{ }}hay{\rm{ }}d' = \frac{{df}}{{d - f}}\]. (Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 182, 187).

Xét trường hợp f = 3, đặt x = d, y = d ′. Ta có hàm số \[y = \frac{{3x}}{{x - 3}}\]và x ≠ 3.

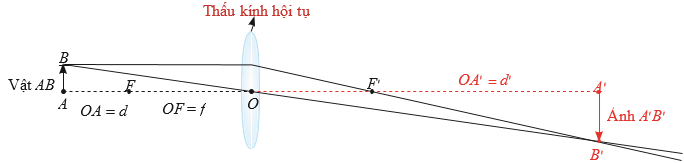
a) Khảo sát và vẽ đồ thị của hàm số trên.

b) Dựa vào đồ thị hàm số trên, hãy cho biết vị trí của vật để ảnh của vật là: ảnh thật, ảnh ảo.

c) Khi vật tiến gần đến tiêu điểm thì ảnh thay đổi như thế nào?

Người ta muốn chế tạo một chiếc hộp hình hộp chữ nhật có thể tích 500 cm3 với yêu cầu dùng ít vật liệu nhất. Chiều cao của hộp phải là 2 cm, các kích thước khác là x, y với x > 0 và y > 0.

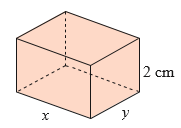
a) Hãy biểu thị y theo x.

b) Chứng tỏ rằng diện tích toàn phần của chiếc hộp là: \[S(x) = 500 + 4x + \frac{{1000}}{x}\]

c) Lập bảng biến thiên của hàm số S(x) trên khoảng (0; +∞).

d) Kích thước của hộp là bao nhiêu thì dùng ít vật liệu nhất? (Làm tròn kết quả đến hàng phần mười.)

Bạn Việt muốn dùng tấm bìa hình vuông cạnh 6 dm làm một chiếc hộp không nắp, có đáy là hình vuông bằng cách cắt bỏ đi 4 hình vuông nhỏ ở bốn góc của tấm bìa (Hình vẽ bên dưới).

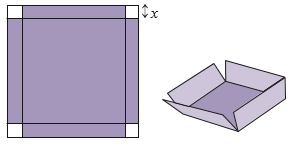
Bạn Việt muốn tìm độ dài cạnh hình vuông cần cắt bỏ để chiếc hộp đạt thể tích lớn nhất.

a) Hãy thiết lập hàm số biểu thị thể tích hộp theo x với x là độ dài cạnh hình vuông cần cắt đi.

b) Khảo sát và vẽ đồ thị hàm số tìm được. Từ đó, hãy tư vấn cho bạn Việt cách giải quyết vấn đề và giải thích vì sao cần chọn giá trị này. (Làm tròn kết quả đến hàng phần mười.)

Trong 20 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức: \[Q(t) =  - \frac{1}{5}{t^3} + 5{t^2} + 100,\] trong đó Q tính theo m3/phút, t tính theo phút, 0 ≤ t ≤ 20 (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến 550 m3/phút thì cảnh báo lũ được đưa ra.

Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điểm nào?

Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được \(x\) mét vải lụa \((1 \le x \le 18)\). Tồng chi phí sản xuất \(x\) mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:

\(C(x) = {x^3} - 3{x^2} - 20x + 500.{\rm{ }}\)

Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 220 nghìn đồng \(/{\rm{mét}}\).

Gọi \(B(x)\) là số tiền bán được và \(L(x)\) là lợi nhuận thu được khi bán \(x\) mét vải lụa.

a) Hãy viết biểu thức tính \(B(x)\) và \(L(x)\) theo \(x\).

b) Khảo sát và vẽ đồ thị của hàm số \(L(x)\) trên [1 ; 18].

c) Hộ làm nghề dệt này cần sản xuất và bán ra mỗi ngày bao nhiêu mét vải lụa để thu được lợi nhuận tối đa? Tính lợi nhuận tối đa đó.

Một bể chứa ban đầu có 200 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 40 lít nước, đồng thời cho vào bể 20 gam chất khử trùng (hoà tan).

a) Tính thể tích nước và khối lượng chất khử trùng có trong bể sau t phút. Từ đó tính nồng độ chất khử trùng (gam/lít) trong bể sau t phút.

b) Coi nồng độ chất khử trùng là hàm số f(t) với t ≥ 0. Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.

c) Hãy giải thích tại sao nồng độ chất khử trùng tăng theo t nhưng không vượt ngưỡng 0,5 gam/lít.

Một cốc chứa 30 ml dung dịch KOH (potassium hydroxide) với nồng độ 100 mg/ml. Một bình chứa dung dịch KOH khác với nồng độ 8 mg/ml được trộn vào cốc.

a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x).

b) Coi C(x) là hàm số xác định với x ≥ 0. Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.

c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8 mg/ml.

Trong Vật lí, ta biết rằng khi mắc song song hai điện trở R1 và R2 thì điện trở tương đương R của mạch điện được tính theo công thức: \[R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\] (theo Vật lí đại cương,NXB Giáo dục Việt Nam, 2016).

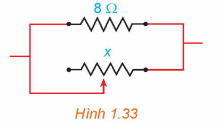
Giả sử một điện trở 8 2 được mắc song song với một biến trở như Hình 1.33. Nếu điện trở đó được kí hiệu là x (\[\Omega \]) thì điện trở tương đương R là hàm số của x. Vẽ đồ thị của hàm số y = R(x), x > 0 và dựa vào đồ thị đã vẽ, hãy cho biết:

a) Điện trở tương đương của mạch thay đổi thế nào khi x tăng.

b) Tại sao điện trở tương đương của mạch không bao giờ vượt quá 8 \[\Omega \].

Một hồ nước nhân tạo được xây dựng trong một công viên giải trí. Trong mô hình minh hoạ (Hình vẽ bên dưới), nó được giới hạn bởi các trục toạ độ và đồ thị của hàm số: \[y = f(x) = \frac{1}{{10}}( - {x^3} + 9{x^2} - 15x + 56)\]. Đơn vị đo độ dài trên mỗi trục toạ độ là 100 m.

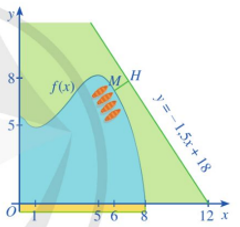
a) Đường dạo ven hồ chạy dọc theo trục Ox dài bao nhiêu mét?

b) Tại những điểm nào trên đường đi dạo ven hồ (chạy dọc theo trục Ox) thì khoảng cách theo phương thẳng đứng đến bờ hồ đối diện là lớn nhất? Tìm khoảng cách lớn nhất đó.

c) Trong công viên có một con đường chạy dọc theo đồ thị hàm số y = – 1,5x + 18. Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nước sao cho khoảng cách từ bến thuyền đến con đường này là ngắn nhất. Tìm toạ độ của điểm để xây bến thuyền này.

Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức: \[f(t) = \frac{{26t + 10}}{{t + 5}}\] (f(t) được tính bằng nghìn người) (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam)

a) Tính số dân của thị trấn vào năm 2022 (làm tròn kết quả đến hàng phần nghìn).

b) Xem y = f(t) là một hàm số xác định trên nửa khoảng \[\left[ {0; + \infty } \right)\]. Khảo sát và vẽ đồ thị hàm số f(t).

c) Đạo hàm của hàm số y=f(t) biểu thị tốc độ tăng dân số của thị trấn (tính bằng nghìn người/năm).

c1) Tính tốc độ tăng dân số vào năm 2022 của thị trấn đó.

c2) Vào năm nào thì tốc độ tăng dân số là 0,192 nghìn người/năm?

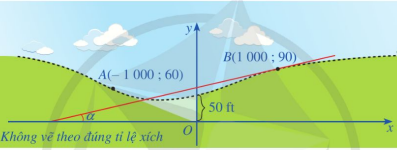
(Bài toán thiết kế mô hình đường giao thông) Để thiết kế mô hình của một đoạn đường cao tốc nối hai sườn đồi với sự khác biệt về độ cao ở vị trí hai sườn đồi giao nhau là 50 feet (Hình vẽ), người ta có thể làm như sau:

• Chọn hệ trục toạ độ Oxy với gốc O là vị trí hai sườn đồi giao nhau, phương nằm ngang là trục Ox, đơn vị trên mỗi trục toạ độ là feet (1 feet = 0,3048 m).

• Chọn hai vị trí A, B lần lượt trên hai sườn đồi. Bằng cách đo đạc tại thực địa, ta xác định được toạ độ của hai điểm A, B và góc dốc a (đơn vị: độ) tại điểm B của sườn đồi. Giả sử ta có A(− 1 000 ; 60), B(1 000 ; 90) và tan\[\alpha \] = 0,04 (Hình 27) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).

• Trong hệ trục toạ độ Oxy, quan sát đường cong (vẽ bằng nét đứt) mô phỏng đoạn đường cao tốc nối hai sườn đồi, đường cong đó gợi nên hình ảnh đồ thị của hàm số bậc ba. Vì thế ta có thể chọn hàm số bậc ba y = f(x) = ax3 + bx2 + cx+d (a ≠ 0) sao cho trong hệ trục toạ độ Oxy, đồ thị của hàm số đó trên đoạn

[− 1 000 ; 1 000] mô phỏng đoạn đường cao tốc cần thiết kế. Ta chọn theo nguyên tắc: Hệ số góc của tiếp tuyến tại B của đồ thị hàm số đó bằng 0,04.

a) Hãy xác định hàm số bậc ba đó.

b) Góc dốc của con đường trên đoạn \[\left[ { - 1000;1000} \right]\] lớn nhất tại điểm nào?

(Bài toán thiết kế mô hình đánh giá kĩ năng) Một trung tâm dạy nghề cần thiết kế mô hình đánh giá kĩ năng của một học viên theo học nghề đánh máy. Người ta có thể làm như sau:

• Để xây dựng mô hình toán học cho bài toán trên, ta sử dụng thống kê. Bằng cách khảo sát tốc độ đánh máy trung bình S (tính bằng từ trên phút) của học viên đó sau 1 tuần học (5 ≤ t ≤ 30), ta thu thập các số liệu thống kê được cho trong Bảng 1 (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).

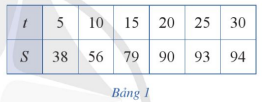
• Ta cần chọn hàm số y = f (t) để biểu diễn các số liệu ở Bảng 1, tức là ở hệ trục toạ độ Oxy, đồ thị của hàm số đó trên khoảng (0 ; + \[\infty \]) “gần” với các điểm A(5 ; 38), B(10 ; 56), C(15 ; 79), D(20 ; 90), E(25 ; 93), G(30 ; 94). Ngoài ra, do tốc độ đánh máy trung bình của học viên tăng theo thời gian t và chỉ đến một giới hạn M nào đó cho dù thời gian t có kéo dài đến vô cùng nên hàm số y = f (t) phải thỏa mãn thêm hai điều kiện: Hàm số đó ĐB trên khoảng (0 ; + \[\infty \]) và \[\mathop {\lim }\limits_{t \to  + \infty } f(t) = M \in \mathbb{R},M > 94\]. Vì các hàm đa thức (với bậc lớn hơn hoặc bằng 1) không thỏa mãn hai điều kiện đó nên ta chọn một hàm phân thức hữu tỉ để biểu diễn các số liệu ở Bảng 1.

Ta có thể chọn hàm số có dạng \[f(t) = \frac{{at + b}}{{ct + d}}\]  (ac ≠ 0) cho mục đích đó. Dựa vào Bảng 1, ta chọn hàm số:

\[f(t) = \frac{{110t - 280}}{{t + 2}},(t > 0)\]

a) Dựa theo mô hình đó, dự đoán tốc độ đánh máy trung bình của học viên đó sau 40 tuần (làm tròn kết quả đến hàng đơn vị của từ/phút)

b) Xem y = f(t) là một hàm số xác định trên khoảng (0 ; + \[\infty \]), hãy tìm tiệm cận ngang của đồ thị hàm số đó.

c) Nêu nhận xét về tốc độ đánh máy trung bình của học viên đó sau thời gian t ngày càng lớn.

Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao h của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm:

h(t) = -0,01t3 + 1,1t2 - 30t+250, trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016).

a) Vẽ đồ thị của hàm số y= h(t) với 0≤ t ≤50 (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 10 km).

b) Gọi v(t) là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với 0 ≤ t ≤50. Xác định hàm số v(t).

c) Vận tốc tức thời của con tàu lúc bắt đầu hãm phanh là bao nhiêu? Tại thời điểm t = 25 (giây) là bao nhiêu?

d) Tại thời điểm t = 25 (giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?

e) Tìm thời điểm t (0 ≤ t ≤50) sao cho con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu?

Xét phản ứng hoá học tạo ra chất C từ hai chất A và B: A+B→ C.

Giả sử nồng độ của hai chất A và B bằng nhau [A] = [B] = a (mol/l). Khi đó, nồng độ của chất C theo thời gian t (t>0) được cho bởi công thức: \[\left[ C \right] = \frac{{{a^2}Kt}}{{aKt + 1}}\] (mol/l), trong đó K là hằng số dương (Nguồn: Đỗ Đức Thái (Chủ biên) và các đồng tác giả, Giáo trình Phép tính vi tích phân hàm một biến, NXB Đại học Sư phạm, 2023).

a) Tìm tốc độ phản ứng ở thời điểm t > 0.

b) Chứng minh nếu x = [C] thì x'(t)=K(a−x)2.

c) Nêu hiện tượng xảy ra với nồng độ các chất khi \[t \to  + \infty \] .

d) Nêu hiện tượng xảy ra với tốc độ phản ứng khi \[t \to  + \infty \] .

Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là C(x) = 2x + 45 (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là \[f(x) = \frac{{C(x)}}{x}\]( coi f(x) là hàm số xác định với x ≥ 1).

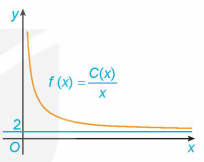
Hãy giải thích tại sao chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/sản phẩm. Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình vẽ như thế nào?

Khi bỏ qua sức cản của không khí, độ cao (mét) của một vật được phóng thẳng đứng lên trên từ điểm cách mặt đất 2 m với vận tốc ban đầu 24,5 m/s là h(t) = 2+24,5t – 4,9t2 (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).

a) Tìm vận tốc của vật sau 2 giây.

b) Khi nào vật đạt độ cao lớn nhất và độ cao lớn nhất đó là bao nhiêu?

c) Khi nào thì vật chạm đất và vận tốc của vật lúc chạm đất là bao nhiêu?

Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số \[P(t) = \frac{a}{{b + {e^{ - 0,75t}}}}\], trong đó thời gian t được tính bằng giờ. Tại thời điểm ban đầu t= 0, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Tìm các giá trị của a và b. Theo mô hình này, điều gì xảy ra với quần thể nấm men về lâu dài?

Giả sử chi phí C(x) (nghìn đồng) để sản xuất x đơn vị của một loại hàng hoá nào đó được cho bởi hàm số C(x)= 30 000 + 300x − 2,5x² + 0,125x³.

a) Tìm hàm chi phí biên.

b) Tìm C'(200) và giải thích ý nghĩa.

c) So sánh C'(200) với chi phí sản xuất đơn vị hàng hoá thứ 201.

Để loại bỏ x% chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là \[C(x) = \frac{{300x}}{{100 - x}}\](triệu đồng), 0 ≤ x <100.

Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = C(x). Từ đó, hãy cho biết:

a) Chi phí cần bỏ ra sẽ thay đổi như thế nào khi x tăng?

b) Có thể loại bỏ được 100% chất gây ô nhiễm không khí không? Vì sao?

Một nhà sản xuất cần làm những hộp hình trụ có thể tích 1 lít. Tìm các kích thước của hộp đựng đề chi phí vật liệu dùng để sản xuất là nhỏ nhất (kết quả được tính theo centimét và làm tròn đến chữ số thập phân thứ hai).

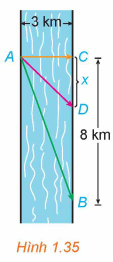
Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3 km và muốn đến điểm B ở bờ đối diện cách 8 km về phía hạ lưu càng nhanh càng tốt (H.1.35). Anh An có thể chèo thuyền trực tiếp qua sông đến điểm C rồi chạy bộ đến B, hoặc anh có thể chèo thuyền thẳng đến B, hoặc anh cũng có thể chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B. Nếu vận tốc chèo thuyền là 6 km/h và vận tốc chạy bộ là 8 km/h thì anh An phải chèo thuyền sang bờ ở điểm nào để đến được B càng sớm càng tốt? (Giả sử rằng vận tốc của nước là không đáng kể so với vận tốc chèo thuyền của anh An).

Nhắc lại rằng nếu C(x) là hàm chi phí, tức là chi phí sản xuất x đơn vị của một sản phẩm nào đó, thì chi phí biên là tốc độ thay đổi của C đối với x, tức là đạo hàm C'(x).

Gọi p(x) là giá bán mỗi đơn vị mà công ty có thể tính nếu bán x đơn vị. Khi đó, p được gọi là hàm cầu (hay hàm giá) và chúng ta mong đợi đó là một hàm giảm của x. Nếu x đơn vị được bán và giá mỗi đơn vị là p(x) thì tổng doanh thu là: R(x) = x. p(x) và R(x) được gọi là hàm doanh thu. Đạo hàm R'(x) của hàm doanh thu được gọi là hàm doanh thu biên và là tốc độ thay đổi của doanh thu đối với số lượng đơn vị sản phẩm bán ra.

Nếu x đơn vị được bán, thì tổng lợi nhuận là P(x) = R(x) - C(x) và P(x) được gọi là hàm lợi nhuận. Hàm lợi nhuận biên là đạo hàm P'(x) của hàm lợi nhuận.

Một nhà phân tích thị trường làm việc cho một công ty sản xuất thiết bị gia dụng nhận thấy rằng nếu công ty sản xuất và bán x chiếc máy xay sinh tố hằng tháng thì lợi nhuận thu được (nghìn đồng) là

P(x) = -0,3x³ +36x² + 1800x-48 000.

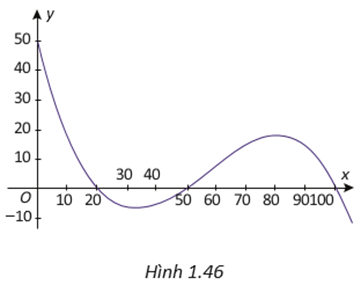
Khảo sát sự biến thiên và vẽ đồ thị hàm số y =P(x), x≥0. Sử dụng đồ thị đã vẽ để trả lời các câu hỏi sau:

a) Khi chỉ sản xuất một vài máy xay sinh tố, công ty sẽ bị lỗ (vì lúc này lợi nhuận âm). Hỏi hằng tháng công ty phải sản xuất ít nhất bao nhiêu chiếc máy xay sinh tố để hoà vốn?

b) Lợi nhuận lớn nhất mà công ty có thể đạt được là bao nhiêu? Công ty có nên sản xuất 200 chiếc máy xay sinh tố hằng tháng hay không?

Khi một vật lạ mắc kẹt trong khí quản khiến ta phải ho, cơ hoành đẩy lên trên gây ra tăng áp lực trong phổi, theo đó cuống họng co thắt làm hẹp khí quản khiến không khí đi qua mạnh hơn. Đối với một lượng không khí bị đẩy ra trong một khoảng thời gian cố định, khí quản càng nhỏ thì luồng không khí càng đẩy ra nhanh hơn. Vận tốc luồng khí thoát ra càng cao, lực tác động lên vật lạ càng lớn. Qua nghiên cứu một số trường hợp, người ta nhận thấy vận tốc v của luồng khí liên hệ với bán kính x của khí quản theo công thức: \[v(x) = k({x_o} - x).{x^2}\] với \[\frac{1}{2}{x_o} \le x \le {x_o}\], trong đó k là hằng số (k > 0) và x0 là bán kính khí quản ở trạng thái bình thường. Tìm x theo x0 để vận tốc của luồng khí một cơn ho trong trường hợp này là lớn nhất. (Nguồn: James Stewart, J. (2015). Calculus. Cengage Learning 8th edition, p.285)

Giả sử chi phí cho xuất bản x cuốn tạp chí (gồm: lương cán bộ, công nhân viên, giấy in,…) được cho bởi công thức:

C(x) = 0,0001x² − 0,2x + 10 000,

trong đó C(x) được tính theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng.

a) Tính tổng chi phí T(x) (xuất bản và phát hành) cho x cuốn tạp chí.

b) Tỉ số \[M(x) = \frac{{T(x)}}{x}\] được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản x cuốn. Tính M(x) theo x và tìm số lượng tạp chí cần xuất bản sao cho chi phí trung bình là thấp nhất, biết rằng nhu cầu hiện tại xuất bản không quá 30 000 cuốn. Khi đó chi phí trung bình cho một cuốn tạp chí là bao nhiêu?

Anh Nam có một mảnh đất rộng và muốn dành ra một khu đất hình chữ nhật có diện tích 200 m² để trồng vài loại cây mới. Anh dự kiến rào quanh ba cạnh của khu đất hình chữ nhật này bằng lưới thép, cạnh còn lại (chiều dài) sẽ tận dụng bức tường có sẵn (Hình vẽ). Do điều kiện địa lí, chiều rộng khu đất không vượt quá 15 m, hỏi chiều rộng của khu đất này bằng bao nhiêu để tổng chiều dài lưới thép cần dùng là ngắn nhất (nghĩa là chi phí rào lưới thép thấp nhất)?

Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) thì chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức:

\[\bar C(x) = 2x - 230 + \frac{{7200}}{x}\]

a) Khảo sát và vẽ đồ thị hàm số \[\bar C(x)\] trên [30; 120].

b) Từ kết quả trên, tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất.

Một phần đường ray tàu lượn siêu tốc có dạng đồ thị hàm số bậc ba: y = f(x) = ax3 + bx2 + cx + d, (\[a \ne 0\]). Trục Ox mô tả quãng đường tàu di chuyển theo chiều ngang (tính bằng centimét), trục Oy mô tả chiều cao của đường ray (tính bằng centimét) tại mỗi vị trí x. Chiều cao xuất phát là 50 cm. Tàu xuống dưới mặt đất lần thứ nhất từ vị trí x = 20 cm, tàu lên khỏi mặt đất ở vị trí x = 50 cm và sau đó xuống dưới mặt đất lần thứ hai ở vị trí x = 100 cm.

Xét đồ thị của hàm số đã cho khi x \[ \in \] [0; 100] như hình vẽ:

a) Tìm công thức hàm số f(x).

b) Tìm điểm cao nhất của đường ray khi tàu lên khỏi mặt đất và toạ độ điểm thấp nhất của đường ray khi tàu xuống dưới mặt đất.

Xét một thấu kính hội tụ có tiêu cự f (Hình vẽ). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức: \[\frac{1}{p} + \frac{1}{q} = \frac{1}{f}\]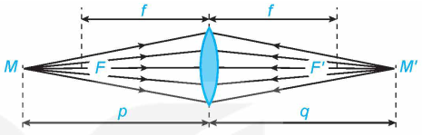

a) Viết công thức tính q = g(p) như một hàm số của biến \[p \in (f; + \infty )\]

b) Tính các giới hạn \[\mathop {\lim }\limits_{p \to  + \infty } g(p);\mathop {\lim }\limits_{p \to {f^ + }} g(p)\]và giải thích ý nghĩa các kết quả này.

c) Lập bảng biến thiên của hàm số q = g(p) trên khoảng \[(f; + \infty )\]

Dân số của một quốc gia sau t (năm) kể từ năm 2023 được ước tính bởi công thức: \[N(t) = 100{e^{0,012t}}\]  (N(t) được tính bằng triệu người, \[0 \le t \le 50\]).

a) Ước tính dân số của quốc gia này vào các năm 2030 và 2035 (kết quả tính bằng triệu người, làm tròn kết quả đến chữ số thập phân thứ ba).

b) Xem N(f) là hàm số của biến số t xác định trên đoạn [0; 50]. Xét chiều biến thiên của hàm số N(t) trên đoạn [0; 50]

c) Đạo hàm của hàm số N(t) biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vào năm nào tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/năm?

Điện trở R (Ω) của một đoạn dây dẫn hình trụ được làm từ vật liệu có điện trở suất ρ (Ωm), chiều dài l (m) và tiết diện S (m2) được cho bởi công thức \[R = \rho .\frac{l}{S}\]

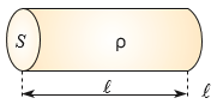(Vật lí 11 – Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 104)

Giả sử người ta khảo sát sự biến thiên của điện trở R theo tiết diện S (ở nhiệt độ 20 oC) của một sợi dây điện dài 10 m làm từ kim loại có điện trở suất ρ và thu được đồ thị hàm số như Hình vẽ bên dướ

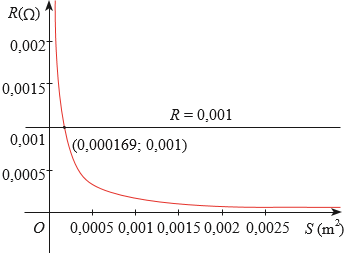
a) Có nhận xét gì về sự biến thiên của điện trở R theo tiết diện S?

b) Từ đồ thị, hãy giải thích ý nghĩa của toạ độ giao điểm của đồ thị hàm số với đường thẳng R = 0,001.

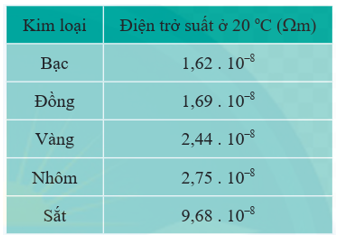
c) Tính điện trở suất ρ của dây điện. Từ đó, hãy cho biết dây điện được làm bằng kim loại nào trong số các kim loại được cho ở bảng sau: