50 CÂU HỎI
Đồ thị của hàm số nào dưới đây có tiệm cận ngang ?
A.
B.
C.
D.
Khối chóp chóp tam giác S.ABC có thể tích V. Gọi M,N,P lần lượt là trung điểm các cạnh SA, SB, SC. Thể tích của khối đa diện ABCMNP bằng
A.
B.
C.
D.
Số phức liên hợp của số phức z=2+3i là
A. 3-2i.
B. 2-3i.
C. -3+2i.
D. -2-3i.
Cho hàm số f (x) có bảng biến thiên như hình vẽ bên
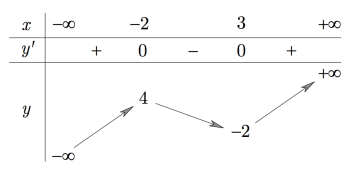
Cực đại của hàm số là
A. -2
B. 4.
C. 3.
D. 2.
Hàm số đồng biến trên khoảng nào dưới đây ?
A. .
B. (0;2).
C. .
D. .
Một tổ hợp chập 2 của tập A={a,b,c,d} là
A. .
B. .
C. (a;b).
D. {a,b}.
Họ các nguyên hàm của hàm số là
A. + C
B. + C
C. + C
D. + C
Cho hai số thực x, y thoả mãn x+y=2. Giá trị của biểu thức bằng
A. 3.
B. 81.
C. .
D. .
Gọi là hai nghiệm phức của phương trình . Tính ||+||.
A. .
B. 3.
C. .
D. 2.
Tập nghiệm của bất phương trình là
A. (-3;3).
B. .
C. (-3;3)\{0}.
D. (-; )\{0}.
Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây ?
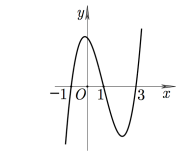
A. .
B. .
C. .
D. .
Thể tích khối tròn xoay tạo thành khi quay quanh trục Ox hình phẳng giới hạn bởi , trục hoành và hai đường thẳng x=0;x=1 là
A.
B.
C.
D.
Trong không gian với hệ toạ độ Oxyz, cho hai véctơ (1;2;-2), (2;-1;2). Tính cos(, ).
A.
B.
C.
D.
Một hình trụ có bán kính đáy bằng 3 và chiều cao bằng 4. Diện tích xung quanh của hình trụ là
A. 36
B. 24
C. 42
D. 33
Trong không gian với hệ toạ độ Oxyz, cho điểm A(2;3;4). Khoảng cách từ A đến trục toạ độ Ox bằng
A. 2.
B. 4.
C. 3.
D. 5.
Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x=-1 là
A. y=-3x-6.
B. y=3x.
C. y=-3x+6.
D. y=3x-6.
Tích phân bằng
A. -2
B. sin1
C. 2
D. -sin1
Giá trị nhỏ nhất của hàm số trên đoạn [-2;-1] bằng
A. -4.
B. -5.
C. -6.
D. -3.
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(0;-1;3), B(1;0;1), C(-1;1;2). Phương trình đường thẳng qua A và song song với BC là
A.
B.
C.
D.
Cho hàm số f (x) có bảng biến thiên như hình vẽ bên
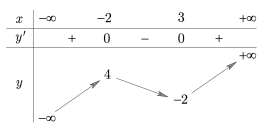
Số nghiệm của phương trình là
A. 2.
B. 4.
C. 3.
D. 1.
Tổng số tiền ông A dùng để trả tiền thuê mặt bằng công ty trong năm 2016 là 300 triệu đồng. Biết rằng cứ sau mỗi năm thì tổng số tiền dùng trả tiền thuê mặt bằng công ty trong cả năm đó tăng thêm 10% so với năm trước. Tổng số tiền ông A dùng để trả tiền thuê mặt bằng công ty trong năm 2018 là
A. 330 triệu đồng.
B. 363 triệu đồng.
C. 399,3 triệu đồng.
D. 360 triệu đồng.
Một nhóm 10 học sinh gồm 6 học sinh lớp A và 4 học sinh lớp B. Chọn ngẫu nhiên 3 học sinh. Xác suất để 3 học sinh được chọn gồm đủ hai lớp A và B bằng
A.
B.
C.
D.
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CA và AD (tham khảo hình vẽ bên). Biết . Góc giữa hai đường thẳng AB và CD là
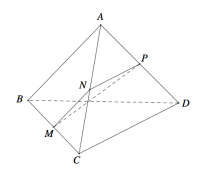
A. 30
B. 45
C. 90
D. 60
Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng trung trực của đoạn thẳng nối hai điểm A(2;1;3),B(-2;1;-1) là
A. y+z-2=0.
B. x-z+1=0.
C. x+z+2=0.
D. x+z-1=0.
Hệ số của số hạng chứa trong khai triển là
A.
B.
C.
D.
Tổng các nghiệm của phương trình là
A. 9.
B. .
C. .
D. 10.
Cho tứ diện OABC có OA,OB,OC đôi một tạo với nhau góc và OA=OB=a,OC=2a. Côsin góc giữa đường thẳng OC và mặt phẳng (ABC) bằng
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 6a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD,d(G,(SAD))=a (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng SD và BC.
A. 2a
B. 3a
C. 4a
D. a
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A,B,C lần lượt di động trên ba trục toạ độ Ox,Oy,Oz (không trùng với gốc toạ độ O) sao cho . Biết mặt phẳng (ABC) luôn tiếp xúc với một mặt cầu cố định. Tính bán kính của mặt cầu đó.
A. 4.
B. 3.
C. 1.
D. 2.
Có bao nhiêu số nguyên dương m để hàm số nghịch biến trên khoảng .
A. 3.
B. 2.
C. 4.
D. 5.
Cho đường cong bậc bốn và đường thẳng có đồ thị như hình vẽ bên. Tính diện tích hình phẳng giới hạn bởi (C) và .
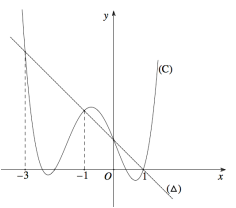
A.
B.
C.
D.
Cho với a,b,c là các số nguyên dương và tối giản. Giá trị biểu thức a+b+c bằng
A. 111.
B. 239.
C. 255.
D. 367.
Có bao nhiêu số nguyên m để phương trình có nghiệm thực.
A. 11.
B. 6.
C. 5.
D. 10.
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA=OB=a,OC=2a. Thể tích khối cầu ngoại tiếp tứ diện OABC bằng
A.
B.
C.
D.
Cho hàm số . Biết . Mệnh đề nào dưới đây đúng ?
A. 0<m<2.
B. -6<m<-3.
C. 2<m<4.
D. -3<m<0.
Có bao nhiêu số nguyên để phương trình có hai nghiệm phân biệt.
A. 2017.
B. 2016.
C. 0.
D. 2015.
Cho hàm số y = f (x) có đồ thị của hàm số y=f'(x) như hình vẽ bên. Hàm số đồng biến trên khoảng nào dưới đây ?
A. .
B. (1;2).
C. .
D. (;1).
Cho hàm số f(x) liên tục trên đoạn [0;2] thoả mãn và f(x)=f(2-x),. Tích phân bằng
A. -40.
B. 20.
C. 40.
D. -20.
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;0;2),B(0;2;-2). Các điểm M, N lần lượt di động trên các đoạn thẳng OA, OB sao cho MN chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi MN ngắn nhất thì toạ độ trọng tâm của tam giác OMN là
A. (; ; 0)
B. (; ; 0)
C. (; ; 0)
D. (; ; 0)
Gọi M,N lần lượt là các điểm biểu diễn số phức . Biết ,||=2,||=6. Tìm phần thực của số phức .
A.
B.
C.
D.
Cho biết có kết quả là một số thực. Giá trị biểu thức a+b bằng
A. = -6
B. = -4
C. = -5
D. = -9
Cho cấp số nhân () có tất cả các số hạng đều dương thoả mãn . Số tự nhiên n nhỏ nhất để là
A. 102.
B. 301.
C. 302.
D. 101.
Cho hàm số có đồ thị (C). Có bao nhiêu giá trị thực của tham số m để (C) có ba điểm cực trị và đường tròn qua ba điểm cực trị này đồng thời đi qua điểm A(;).
A. 3.
B. 1.
C. 4.
D. 2.
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;1;0),B(0;1;1),C(2;1;2) và mặt phẳng (P):x+y-z-6=0. Điểm M(a;b;c) thuộc (P) sao cho đạt giá trị nhỏ nhất. Giá trị biểu thức ab+bc+ca bằng
A.
B.
C.
D.
Cho số phức z thoả mãn . Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức Tính giá trị của biểu thức
A.
B.
C.
D.
Cho hàm số f (x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(1)=1 và ,. Tích phân bằng
A.
B.
C.
D.
Cho khối hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, AB=, AD=. Hai mặt bên (ABB'A'),(ADD'A') tạo với đáy các góc lần lượt là và . Tính thể tích V của khối hộp đã cho biết độ dài cạnh bên bằng 1.
A. V = 3
B. V =
C. V =
D. V =
Cho hình chóp S.ABC có AB=2a,BC=a,. Biết mặt phẳng (SAC) vuông góc với mặt phẳng (ABC),d(C,SA)=2. Côsin góc giữa hai mặt phẳng (SAC) và (SAB) bằng
A.
B.
C.
D.
Trong một lớp có 45 học sinh, trong đó có ba bạn A,B,C cùng 42 học sinh khác. Khi xếp tuỳ ý 45 học sinh này vào một dãy ghế dài có đánh số từ 1 đến 45(mỗi học sinh ngồi một ghế). Xác suất để số ghế của A bằng trung bình cộng số ghế của B và C bằng
A.
B.
C.
D.
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(-2;0;0),B(0;-2;0),C(0;0;-2). Các điểm M, N, P lần lượt trên ba cạnh OA, OB, OC sao cho và khối tứ diện OMNP có thể tích nhỏ nhất. Mặt phẳng :ax+by+cz-1=0 đi qua ba điểm M, N, P. Tính S=a+b+c.
A. S =
B. S = -4
C. S = -2
D. S = -3


