50 CÂU HỎI
Cho số phức z thỏa mãn điều kiện Tìm phần ảo của số phức .
A. -i
B. -1
C. 2
D. -2i
Cho số phức z thỏa mãn điều kiện Tìm phần ảo của số phức .
A. -i
B. -1
C. 2
D. -2i
Tìm tất cả các giá trị của tham số thực m để phương trình sau có đúng 3 nghiệm thực phân biệt
A. m =
B. 2 < m <
C. m = 2
D. m < 2
Một người thả 1 lá bèo vào một cái ao, sau 12 giờ thì bèo sinh sôi phủ kín mặt ao. Hỏi sau mấy giờ thì bèo phủ kín mặt ao, biết rằng sau mỗi giờ thì lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi.
A. (giờ)
B. (giờ)
C. (giờ)
D. (giờ)
Tập giá trị của m thỏa mãn bất phương trình là . Khi đó a + b + c bằng:
A. 3
B. 1
C. 2
D. 0
Cho hàm số y = f(x) xác định trên R\{-1}, liên tục trên các khoảng xác định của nó và có bảng biến thiên như hình vẽ:

Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có 3 tiệm cận.
B. Phương trình f(x) = m có 3 nghiệm thực phân biệt thì
C. Giá trị lớn nhất của hàm số là 2
D. Hàm số đồng biến trên
Cho . Hãy tính theo a, b
A.
B.
C.
D.
Cho . Tính giá trị P =
Chọn đáp án đúng.
A. P = 2 -
B. P = 2 +
C. P = 3 +
D. P = 3 -
Cho phương trình: cosx + sin4x - cos3x = 0. Phương trình trên có bao nhiêu họ nghiệm ?
A. 2
B. 6
C. 3
D. 5
Gọi lần lượt là tập nghiệm của các bất phương trình sau: . Tìm khẳng định đúng?
A.
B.
C.
D.
Tìm GTLN và GTNN của hàm số là:
A.
B.
C.
D.
Cho hai số phức và . Tính môđun của số phức .
A.
B. 5
C.
D.
. Điều kiện xác định của hàm số là:
A.
B.
C.
D.
Biết , trong đó a, b, c là các số nguyên dương và là phân số tối giản. Tính S = a + b + c.
A. S = 60
B. S = 70
C. S = 72
D. S = 68
Parabol chia hình tròn có tâm là gốc tọa độ, bán kính bằng thành hai phần có diện tích là và , trong đó . Tìm tỉ số
A.
B.
C.
D.
Số nghiệm của phương trình là:
A. 1
B. 3
C. 0
D. 2
Một đội ngũ giáo viên gồm 8 thầy giáo dạy toán, 5 cô giáo dạy vật lý và 3 cô giáo dạy hóa học. Sở giáo dục cần chọn ra 4 người để chấm bài thi THPT quốc gia, tính xác suất trong 4 người được chọn phải có cô giáo và có đủ ba bộ môn
A.
B.
C.
D.
Cho điểm M(-3; 2; 4), gọi A, B, C lần lượt là hình chiếu của M trên trục Ox, Oy, Oz. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (ABC).
A. 6x - 4y - 3z - 12 = 0
B. 3x - 6y - 4z + 12 = 0
C. 4x - 6y - 3z + 12 = 0
D. 4x - 6y - 3z - 12 = 0
Giải bất phương trình:
A.
B.
C.
D.
Cho khai triển: biết ba hệ số đầu tiên lập thành cấp số cộng. Tìm các số hạng của khai triển nhận giá trị hữu tỷ
A.
B.
C. A và B
D. Không có đáp án nào
Giá trị cực đại của hàm số y = x + sin2x trên là:
A.
B.
C.
D.
Tìm tập xác định của hàm số
A.
B.
C.
D.
Cho mặt cầu và mặt phẳng (): 2x+y-2z+m=0. Các giá trị của m để () và (S) không có điểm chung là:
A. hoặc
B. hoặc
C.
D.
Giới hạn bằng (phân số tối giản). Giá trị của a - b là:
A. 1
B.
C. -1
D.
Tìm nguyên hàm của hàm số y = f(x) = .
A.
B.
C.
D.
Cho hình chóp tam giác đều S.ABC có đường cao SO = a, . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng:
A.
B.
C.
D.
Trong không gian cho hình chữ nhật ABCD có AB = 1. AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó?
A.
B.
C.
D.
Cho hàm số . Đồ thị hàm số có bao nhiêu tiệm cận ?
A. 2
B. 3
C. 4
D. 5
Một chất điểm đang cuyển động với vận tốc thì tăng vận tốc với gia tốc . Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng vận tốc.
A. 68,25m
B. 70,25m
C. 69,75m
D. 67,25m
Cho số phức thỏa mãn . Tính giá trị biểu thức P = a - b.
A. P = 5
B. P = -2
C. P = 3
D. P = 1
Cho số phức z và số phức liên hợp của nó có điểm biểu diễn là M, M’. Số phức và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức .
A.
B.
C.
D.
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A; AB = 2, AC = 3. Mặt phẳng (A'BC) hợp với (A'B'C') góc . Thể tích lăng trụ đã cho bằng bao nhiêu?
A.
B.
C.
D.
Cho hàm số . Giá trị lớn nhất của hàm số trên là:
A.
B.
C. 2
D. 3
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên . Khẳng định nào sau đây là khẳng định đúng?
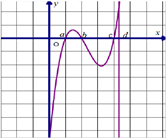
A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Nếu lập thành một cấp số cộng (theo thứ tự đó) thì dãy số nào sau đây lập thành một cấp số cộng?
A.
B.
C.
D.
Cho các hàm số: , .Tính biểu thức: 3f'(x) - 2g'(x) + 2
A. 0
B. 2
C. 1
D. 3
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): . Mệnh đề nào đúng?
A. Mặt cầu (S) tiếp xúc với (Oxy)
B. Mặt cầu (S) không tiếp xúc với cả ba mặt (Oxy), (Oxz), (Oyz)
C. Mặt cầu (S) tiếp xúc với (Oyz)
D. Mặt cầu (S) tiếp xúc với (Oxz)
Cho điểm M(3; 2; 1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz tại A, B, C sao cho M là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là:
A.
B. x + y + z - 6 = 0
C. 3x + 2y + z - 14 = 0
D.
Hàm số đồng biến trên thì giá trị của m là:
A. m
B. m
C. m
D. m
Gọi I là tâm mặt cầu đi qua 4 điểm M(1; 0; 0), N(0; 1; 0), P(0; 0; 1), Q(1; 1; 1). Tìm tọa độ tâm I.
A.
B.
C.
D.
Hàm số có ba điểm cực trị và đường tròn đi qua ba điểm cực trị này có bán kính bằng 1 thì giá trị của m là:
A. m = 1; m =
B. m = -1; m =
C. m = 1; m =
D. m = 1; m =
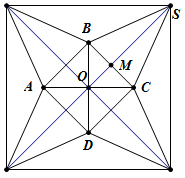
Cho hình chóp tứ giá đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc . Gọi M là điểm đối xứng của C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng:
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x + y - 3z +2 = 0. Viết phương trình mặt phẳng (Q) song song và cách (P) một khoảng bằng .
A. -4x - 2y + 6z + 7 = 0; 4x + 2y - 6z + 15 = 0
B. -4x - 2y + 6z - 7 = 0; 4x + 2y - 6z + 5 = 0
C. -4x - 2y + 6z + 5 = 0; 4x + 2y - 6z - 15 = 0
D. -4x - 2y + 6z + 3 = 0; 4x + 2y - 6z - 15 = 0
Cho tứ diện S.ABC trên cạnh SA và SB lấy điểm M và N sao cho thỏa tỉ lệ , mặt phẳng đi qua MN và song song với SC chia tứ diện thành hai phần, biết tỉ số thể tích của hai phần ấy là K, vậy K là giá trị nào?
A. K =
B. K =
C. K =
D. K =
Thể tích khối tròn xoay do hình phẳng được giới hạn bởi các đường và quay quanh trục Ox bằng bao nhiêu?
A.
B.
C.
D.
Đạo hàm của hàm số là:
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c dương. Biết A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c = 2. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016; 0; 0) tới mặt phẳng (P).
A. 2017
B.
C.
D.
Gọi là bốn nghiệm phức của phương trình . Trên mặt phẳng tọa độ, gọi A, B, C, D lần lượt là bốn điểm biểu diễn bốn nghiệm đó. Tính giá trị của P = OA + OB + OC + OD, trong đó O là gốc tọa độ.
A. P = 4
B. P =
C. P =
D. P =
Một hình hộp ABCD.A’B’C’D’ có thể tích bằng V. Khi đó, thể tích tứ diện A’C’BD.
A.
B.
C.
D.
Người ta cắt một tờ giấy hình vuông có cạnh bằng để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất.
A.
B.
C. 1
D.


