50 CÂU HỎI
Diện tích hình phẳng giới hạn bởi đường cong và đường thẳng bằng S là
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(−2;3;4), gọi A, B, C lần lượt là hình chiếu của M trên Ox, Oy, Oz. Mặt phẳng nào sau đây song song với mặt phẳng (ABC)?
A.
B.
C.
D.
bằng
A. 0
B. 1,499
C.
D.
Tính tích phân
A.
B.
C. 1
D.
Số nghiệm của phương trình là
A. 1
B. 2
C. Đáp án khác
D. 0
Cho số phức Phần thực của số phức z là
A.
B.
C.
D.
Đồ thị hàm số có tâm đối xứng là điểm nào?
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxyz cho A(1;1;0), B(2;−1;1), C(3;−1;1). Tính diện tích S của tam giác ABC.
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxyz cho A(−1;2;0),B(−2;0;2). Viết phương trình đường thẳng AB.
A.
B.
C.
D.
Đồ thị trong hình vẽ là đồ thị của hàm số nào sau đây
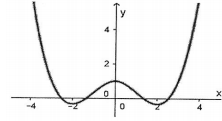
A.
B.
C.
D.
Cho đường tròn . Tính diện tích hình tròn (C’).
A.
B.
C.
D.
Cho hàm số Số giao điểm của đồ thị hàm số và trục hoành là
A. 3
B. 0
C. 1
D. 2
Cho Giá trị của tỷ số là
A.
B.
C.
D.
Cho hàm số có đạo hàm Hỏi đồ thị hàm số có bao nhiêu điểm cực trị?
A. 1
B. 2
C. 3
D. 4
Đồ thị hàm số có bao nhiêu tiệm cận đứng?
A. 2
B. 1
C. 0
D. 3
Gọi L là chiều dài của đoạn đường có điểm đầu là A và điểm cuối B (hình vẽ là những nửa đường tròn đồng tâm O và có bán kính lần lượt là 1,2,3,4,5). Hãy chọn khẳng định đúng.
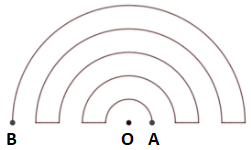
A. 47
B. L<50
C. 51
D. L>52
Cho tam giác ABC vuông tại A, AB = a, góc ABC bằng Quay miền trong tam giác ABC quanh cạnh BC ta được một khối tròn xoay, tính thể tích khối đó?
A.
B.
C.
D.
Hàm số F(x) là một nguyên hàm của hàm số và F(3) = 0 thì
A.
B.
C.
D.
Cho Tiếp tuyến của (C) song song với đường thẳng có phương trình là
A.
B.
C.
D.
Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thỏa mãn điều kiện là hình gì?
A. Một đường Elip
B. Một đường tròn
C. Một đường thẳng
D. Một đường Parabol
Cho 2 số thực x,y thỏa phương trình Khi đó có giá trị là
A.
B.
C. 1
D.
Gọi A,B,C lần lượt là các điểm biểu diễn cho các số phức Chọn kết luận đúng nhất.
A. Tam giác ABC vuông cân tại A
B. Tam giác ABC cân tại B
C. Tam giác ABC vuông cân tại B
D. Tam giác ABC cân tại A
Trong không gian Oxyz, cho ba điểm A(1;−1;1),B(1;3;1),C(4;−1;−2). Tâm đường tròn ngoại tiếp tam giác ABC có tọa độ là
A.
B.
C.
D.
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường , quanh trục Ox là
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a; SA = 2a và vuông góc với đáy. Khoảng cách từ điểm A tới mặt phẳng (SBD) là
A.
B.
C.
D.
Cho lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng Tính thể tích của khối lăng trụ.
A.
B.
C.
D.
Giả sử hai nghiệm của phương trình là Khi đó có giá trị là
A. 6
B. -4
C. 7
D. -5
Gọi là hai nghiệm phức của phương trình Giá trị của biểu thức bằng
A.
B. 4
C. 2
D. 1
Đường tiệm cận xiên của đồ thị hàm số tạo với hai trục tọa độ một tam giác có diện tích bằng
A.
B.
C.
D.
Cho x là số thực dương thỏa mãn . Tính giá trị của
A. 0
B. 0 và -1
C. 0 và 1
D. 1
Đạo hàm của hàm số là
A.
B.
C.
D.
Tìm m để hàm số liên tục tại điểm
A.
B.
C.
D.
Một hình lăng trụ có đáy là tam giác đều cạnh a, cạnh bên bằng b và tạo với mặt phẳng đáy một góc α. Thể tích của lăng trụ đó là
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxy cho A(1;2;0),B(−1;0;2). Viết phương trình mặt cầu (S) tâm A và bán kính AB.
A.
B.
C.
D.
Số véctơ khác có điểm đầu và điểm cuối là hai trong 6 đỉnh của lục giác ABCDEF là
A.
B. 36
C.
D.
Một nguyên hàm của hàm số là
A.
B.
C.
D.
Kết luận nào sau đây là đúng về m? Biết .
A. m không phải số nguyên tố cũng không phải hợp số
B. m là số nguyên tố
C. m là hợp số
D. m vừa là số nguyên tố vừa là hợp số
Thầy giáo dạy Toán gửi 300 triệu đồng vào ngân hàng với lãi suất 6,8% năm, phương thức tính lãi 3 tháng một lần. Hỏi sau 3 năm 6 tháng thầy giáo nhận được bao nhiêu tiền cả vốn lẫn lãi, biết thầy chưa rút lãi lần nào.
A. 380 triệu đồng
B. 349 triệu đồng
C. 375 triệu đồng
D. 354 triệu đồng
Tính tổng tất cả các giá trị nguyên của hàm số
A. 3
B. 6
C. 8
D. 5
Nếu và thì giá trị của ab là
A.
B.
C.
D.
Giá trị lớn nhất của hàm số là
A. 5
B. 2
C. 0
D. 4
Rút gọn biểu thức
A.
B.
C.
D.
Cho hình chóp S.ABC có , Tính thể tích hình chóp S.ABC.
A.
B.
C.
D.
Cho đa giác đều 20 đỉnh. Lấy ngẫu nhiên 3 đỉnh. Tính xác suất để 3 đỉnh đó là 3 đỉnh của một tam giác vuông không cân.
A.
B.
C.
D.
Số nghiệm của phương trình trong đoạn là
A. 2
B. 3
C. 1
D. 4
Cho một hình trụ có chiều cao và bán kính đều bằng a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ. Tính cạnh của hình vuông này.
A. a
B. 2a
C.
D.
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông. AB = BC = a, cạnh bên AA’=. Gọi M là trung điểm cạnh BC. Tính theo a khoảng cách giữa hai đường thẳng AM và B’C.
A.
B.
C.
D.
Cho tứ diện đều ABCD cạnh a. Tính diện tích mặt cầu nội tiếp tứ diện ABCD.
A.
B.
C.
D. Đáp án khác
Trên một đoạn đường giao thông có hai con đường vuông góc với nhau tại O như hình vẽ. Một địa danh có vị trí đặt tại M , vị trí M cách đường Oy 216m và cách đường Ox 1000m. Vì lý do thực tiễn, người ta muốn làm một đoạn đường thẳng AB đi qua vị trí M, biết rằng giá để làm 100m đường là 200 triệu đồng. Chọn vị trí của A và B để hoàn thành con đường với chi phí thấp nhất. Hỏi chi phí thấp nhất để hoàn thành con đường là bao nhiêu?
A. 2,093 tỷ đồng
B. 3,172 tỷ đồng
C. 1,967 tỷ đồng
D. 2,153 tỷ đồng
Hình chóp S.ABC có đáy là tam giác vuông tại B có AB=a, AC=2a, SA vuông góc với mặt phẳng đáy, SA=2a. Gọi α là góc tạo bởi hai mặt phẳng (SAC) và (SBC). Tính .
A.
B.
C.
D.


