49 CÂU HỎI
Đường cong ở hình bên là đồ thị
của hàm số nào dưới đây
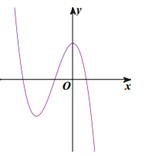
A.
B.
C.
D.
Bảng biến thiên dưới đây là của hàm số nào
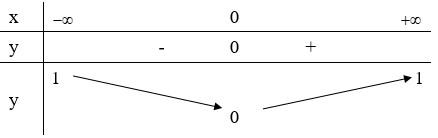
A.
B.
C.
D.
Cho và , khẳng định nào dưới đây là khẳng định đúng?
A. a > 1, 0 < b < 1
B. 0 < a < 1, 0 < b < 1
C. a > 1, b > 1
D. 0 < a < 1, b > 1
Căn bậc hai phức của -20 là
A.
B.
C.
D.
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, SA = a. Thể tích V của khối chóp SBCD là
A.
B.
C.
D.
Hỏi hàm số đồng biến trên khoảng nào sau đây?
A.
B.
C.
D.
Giá trị cực tiểu của hàm số là
A. -3
B. -1
C. 3
D. 1
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là.
A. Tiệm cận đứng x=0 và tiệm cận ngang y=0
B. Tiệm cận đứng x=0 và tiệm cận ngang y=-3
C. Tiệm cận đứng x=0 và không có tiệm cận ngang
D. Tiệm cận đứng x=0 và tiệm cận ngang y=1
Giá trị lớn nhất của hàm số là.
A. Maxy=1
B. Maxy=10
C. Maxy=4
D. Maxy=-1
Tọa độ giao điểm của đồ thị hai hàm số là.
A.
B.
C.
D.
Tất cả các nghiệm của phương trình là
A. x = 2
B. x = 3
C. x = 1
D. x = 1, x = 2
Nghiệm của phương trình là
A.
B.
C.
D.
Nghiệm của bất phương trình là
A.
B.
C.
D.
Cho , khẳng định nào dưới đây là khẳng định đúng?
A. f'(2) = 1
B. f'(2) = 0
C. f'(2) = 1,2
D. f'(2) = -1,2
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có
đồ thị y=f'(x) như hình vẽ bên. Đặt biết rằng
đồ thị của hàm g(x) luôn cắt trục hoành tại 4 điểm phân biệt.
Mệnh đề nào dưới đây đúng
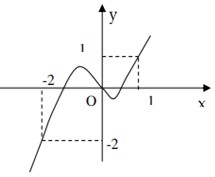
A.
B.
C.
D.
Cho hàm số Tìm m để f(x) liên tục tại
A.
B.
C.
D.
Có bao nhiêu số thực thuộc thỏa mãn
A. 6
B. 5
C. 4
D. 3
Cho Tính a+2b-c
A. T = 7
B. T = -7
C. T = 6
D. T = -6
Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Cho f(x), f(-x) liên tục trên R và thỏa mãn Tính A.
A.
B.
C.
D.
Cho hàm số y=f(x) liên tục trên R và hàm số có đồ thị trên đoạn [0; 2] như hình vẽ bên. Biết diện tích S của miền được tô đậm bằng 5/2, tính tích phân

A. 5/4
B. 5/2
C. 5
D. 10
Cho số phức z là
A.
B.
C.
D.
Cho hai số phức Mô đun của số phức là
A.
B.
C.
D.
Phần thực và ảo của số phức là
A. Phần thực bằng 8 và Phần ảo bằng 8.
B. Phần thực bằng -8 và Phần ảo bằng -8
C. Phần thực bằng 8 và Phần ảo bằng -8
D. Phần thực bằng -8 và Phần ảo bằng 8
Nghiệm của phương trình trên tập số phức là.
A.
B.
C.
D.
Cho lăng trụ đứng =ABCA'B'C' có đáy ABC là tam giác cân tại A, .Thể tích V của khối chóp A.A'ACC' là.
A.
B.
C.
D.
Thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a là.
A.
B.
C.
D.
Khi tăng bán kính của mặt cầu lên hai lần thì thể tích của khối cầu giới hạn bởi mặt cầu đó tăng lên.
A. 2 lần
B. 4 lần
C. 6 lần
D. 8 lần
Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là
A. 2/3
B. 3
C. 1
D. 1/2
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; 0; 2), B(3; 0; 5), C(1; 1; 0). Tọa độ của điểm D sao cho ABCD là hình bình hành là
A. D(4; 1; 3)
B. D(-4; -1; -3)
C. D(2; 1; -3)
D. D(-2; 1; -3)
Trong không gian Oxyz, cho mặt phẳng (P): 2x + y + 2z + 2 =0 và cho mặt cầu Bán kính của đường tròn giao tuyến giữa (P) và (S) là
A.
B.
C.
D.
Trong không gian Oxyz, cho A(1; 2; 1) và đường thẳng . Phương trình mặt thẳng chứa A và d là
A. 7x + 4y - 5z - 10 = 0
B. x + 2y + 3z - 8 = 0
C. x - 2y - z - 3 = 0
D. -x + 2y + z +3 = 0
Trong không gian Oxyz, cho hai mặt phẳng (P): x + y - z + 5 = 0 và (Q): 2x + 2y - 2z + 3 =0. Khoảng cách giữa (P) và (Q) là.
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng và cho mặt phẳng (P): x + y + z -4 = 0. Khẳng định nào dưới đây là khẳng định đúng?
A.
B.
C.
D.
Tìm m để phương trình có duy nhất một nghiệm thuộc khoảng
A.
B.
C.
D.
Cho hàm số với m làm tham số, m>0
Đặt Mệnh đề nào dưới đây đúng
A.
B.
C.
D.
Biết và thỏa mãn Tính
A.
B.
C.
D.
Người ta xếp các hình vuông kề với nhau như hình vẽ dưới đây, mỗi hình vuông có độ dài cạnh bằng nửa độ dài cạnh của hình vuông trước nó. Nếu biết hình vuông đầu tiên có cạnh dài 10 cm thì trên tia Ax cần có một đoạn thẳng dài bao nhiêu cm để có thể xếp được tất cả các hình vuông đó.

A. 30 cm
B. 20 cm
C. 80 cm
D. 90 cm
Tìm các giá trị của x trong khai triển biết rằng số hạng thứ 6 trong khai triển bằng 21 và theo thứ tự lập thành một cấp số cộng
A. x= 4, x= 7
B. x= 3, x= 5
C. x= 0, x= 2
D. x= 2
Diện tích S của hình phẳng giới hạn bởi các đường là.
A. S=e-3
B. S=e+3
C. S=3-e
D. S=6
Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường và trục hoành là
A.
B.
C.
D.
Có 5 người nam và 3 người nữ cùng đến dự tiệc, họ không quen biết nhau, cả 8 người cùng ngồi một cách ngẫu nhiên vào xung quanh một cái bàn tròn có 8 ghế. Gọi p là xác suất không có 2 người nữ nào ngồi cạnh nhau. Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của AB, AD. Khoảng cách h từ điểm D tới mặt phẳng (SCN) là
A.
B.
C.
D.
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của hình nón đỉnh S đáy là hình tròn tâm O' là. (biết thể tích của nó bằng 1/8 thể tích khối nón đỉnh S, đáy là hình tròn tâm O).
A. h=5
B. h=10
C. h=20
D. h=40
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(3;3;1), B(0;2;1) và mặt phẳng (P): x+y+z-7=0. Phương trình đường thẳng d nằm trong (P) sao cho mọi điểm nằm trên d luôn cách đều A, B là
A.
B.
C.
D.
Trong không gian Oxyz, cho A(1;2;1) và đường thẳng . Phương trình đường thẳng đi qua A cắt và vuông góc với d là
A.
B.
C.
D.
Cho tứ diện ABCD có AC=AD=BC=BD, AB=a, CD= Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó
A.
B.
C.
D.
Một con cá bơi ngược dòng sông để vượt một quãng đường là 300 km. Vận tốc chảy của dòng nước là 6 km/h. Gọi vận tốc bơi của cá khi nước đứng yên là v (km/h) và khi đó năng lượng tiêu hao của cá trong t giờ được tính theo công thức trong đó k là hằng số. Vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao ít nhất là.
A. 6 km/h
B. 9 km/h
D. 12 km/h
D. 15 km/h
AB là đoạn vuông góc chung của 2 đường thẳng chéo nhau, M là điểm di động trên , N là điểm di động trên . Đặt AM=m, AN=n . Giả sử ta luôn có với b>0, b không đổi. Xác định m, n để độ dài đoạn MN đạt giá trị lớn nhất
A.
B.
C.
D.


