51 CÂU HỎI
Tập nghiệm của bất phương trình là
A.
B.
C.
D.
Tích tất cả các nghiệm của phương trình bằng
A. 8
BB. 6
C. 16
D. 2
Cho . Khẳng định nào dưới đây đúng?
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng . Hỏi d đi qua điểm nào trong các điểm sau:
A.
B.
C.
D.
Cho khối chóp S.ABC có đáy là tam giác vuông cân tại A, AB = 2, SA vuông góc với đáy và SA = 3 (tham khảo hình bên).
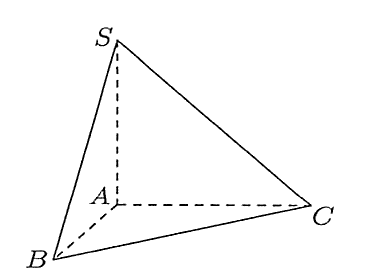
Thể tích khối chóp đã cho bằng
A. 12.
B. 2.
C. 6.
D. 4.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
.
Tính bán kính r của mặt cầu.
A.
B.
C.
D.
Cho một tổ có 15 thành viên. Số cách chọn ra 2 người lần lượt làm tổ trưởng và tổ phó là
A. 225
B. 30
C. 210
D. 105
Trong không gian Oxyz, cho điểm A (1;2;3). Điểm đối xứng với A qua mặt phẳng (Oyz) có tọa độ là
A. (1;-2;3)
B. (1;2;-3)
C. (-1;-2;-3)
D. (-1;2;3)
Trong không gian Oxyz, mặt phẳng (P): x – 2z + 3 = 0 có một vectơ pháp tuyến là:
A.
B.
C.
D.
Đạo hàm của hàm số là:
A.
B.
C.
D.
Trong không gian Oxyz, cho hai điểm M(1;-1;-1) và N(5;5;1). Đường thẳng MNcó phương trình là:
A.
B.
C.
D.
Cho hàm số có đồ thi là đường cong trong hình bên.
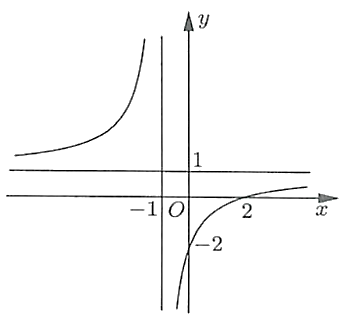
Toạ độ giao điểm của đồ thị hàm số đã cho và trục tung là:
A. (0;-2)
B. (2;0)
C. (-2;0)
D. (0;2)
Cho hàm số y = f(x) xác định và liên tục trên đoạn có [-2;2] và có đồ thị là đường cong trong hình vẽ bên.
![Cho hàm số y = f(x) xác định và liên tục trên đoạn có [-2;2] và có đồ thị là đường cong trong hình vẽ bên. Giá trị cực tiểu của hàm số y = f(x) là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/02/3-1709007069.png)
Giá trị cực tiểu của hàm số y = f(x) là:
A. -4
B. -2
C. (1;-2)
D. x = 1
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên.
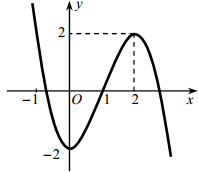
Có bao nhiêu giá trị nguyên của tham số m để phương trình f(x) = mcó ba nghiệm thực phân biệt?
A. 2
B. 5
C. 3
D. 4
Cho hàm số y = f(x) liên tục trên đoạn [a;b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng là:
A.
B.
C.
D.
Trên tập , đạo hàm của hàm số là:
A.
B.
C.
D.
Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
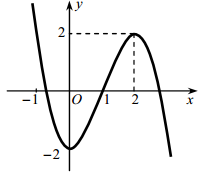
A. (-2;2)
B.
C. (0;2)
D.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
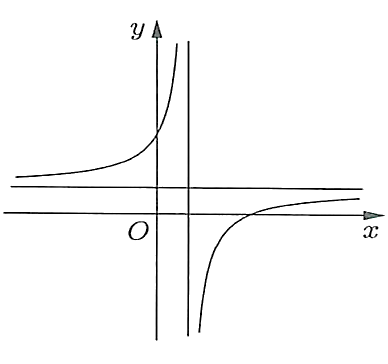
A.
B.
C.
D.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A.
B.
C.
D.
Trong không gian Oxyz, cho mặt cầu . Tâm của (S) có tọa độ là
A. (-1;-2;-3)
B. (2;4;6)
C. (2;3;4)
D. (1;2;3)
Cho hàm số có đồ thị là đường cong trong hình bên dưới.
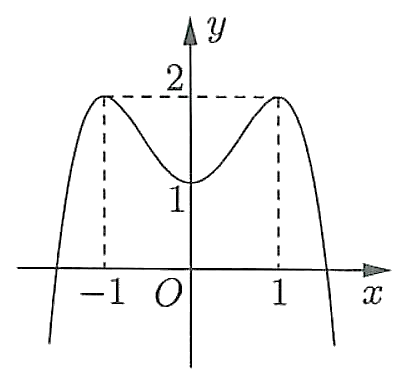
Điểm cực tiểu của hàm số đã cho là
A.
B.
C. (1;2)
D. (0;1)
Cho cấp số nhân với và công bội . Giá trị của bằng
A. 3
B.
C.
D.
Cho cấp số nhân với và công bội . Giá trị của bằng
A. 3
B.
C.
D.
Cho hình trụ có đường kính đáy 2r và độ dài đường sinh l. Diện tích xung quanh của hình trụ đã cho bằng
A.
B.
C.
D.
Cho khối lập phương có cạnh bằng 4. Thể tích của khối lập phương đã cho bằng
A.16
B. 8
C. 4
D. 64
Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức z thỏa mãn là một đường tròn. Tâm của đường tròn đó có tọa độ là
A. (0;2)
B. (-2;0)
C. (0;-2)
D. (2;0)
Tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình
A.
B.
C.
D.
Tập nghiệm của bất phương trình là
A.
B.
C.
D.
Giả sử và . Khi đó bằng
A. I = 11
B. I = 17
C. I = 23
D. I = 8
Trên mặt phẳng tọa độ, điểm biểu diễn số phức có tọa độ là
A. (-6;7)
B. (6;7)
C. (7;6)
D. (7;-6)
Họ nguyên hàm của hàm số là
A.
B.
C.
D.
Cho hàm số y = f(x) có đạo hàm với mọi . Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
B.
C.
D.
Trong không gian Oxyz, góc giữa hai mặt phẳng (Oxy) và (Oyz) bằng
A.
B.
C.
D.
Với a,b là các số thực dương tùy ý và , bằng
A.
B.
C.
D.
Trong hình vẽ bên, điểm M biểu diễn số phứcz.
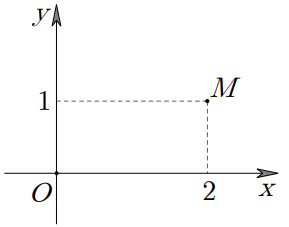
Số phức là
A.
B.
C.
D.
Cho số phức , phần ảo của số phức bằng
A. 36
B. 36i
C. 18
D. 9
Cho hình chóp S.ABC có ; tam giác ABC đều cạnh a và SA = a. Tìm góc giữa SC và mặt phẳng (ABC).
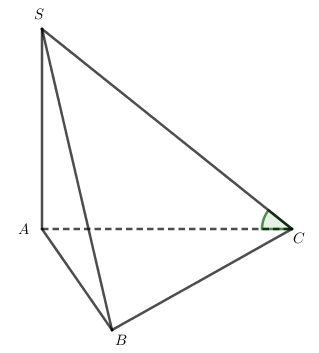
A.
B.
C.
D.
Giải bóng đá Mini cấp trường của một trường THPT, có 16 đội đăng kí tham dự trong đó có 3 đội 12A1, 12A2 và 12A3. Ban tổ chức cho bốc thăm ngẫu nhiên để chia đều 16 đội vào 4 bảng (mỗi bảng 4 đội) để đá vòng loại. Tính xác suất để 3 đội của 3 lớp 12A1, 12A2 và 12A3 nằm ở 3 bảng khác nhau.
A.
B.
C.
D.
Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh a, và (tham khảo hình bên dưới). Khoảng cách từ điểm A đến mặt phẳng (SCD) là
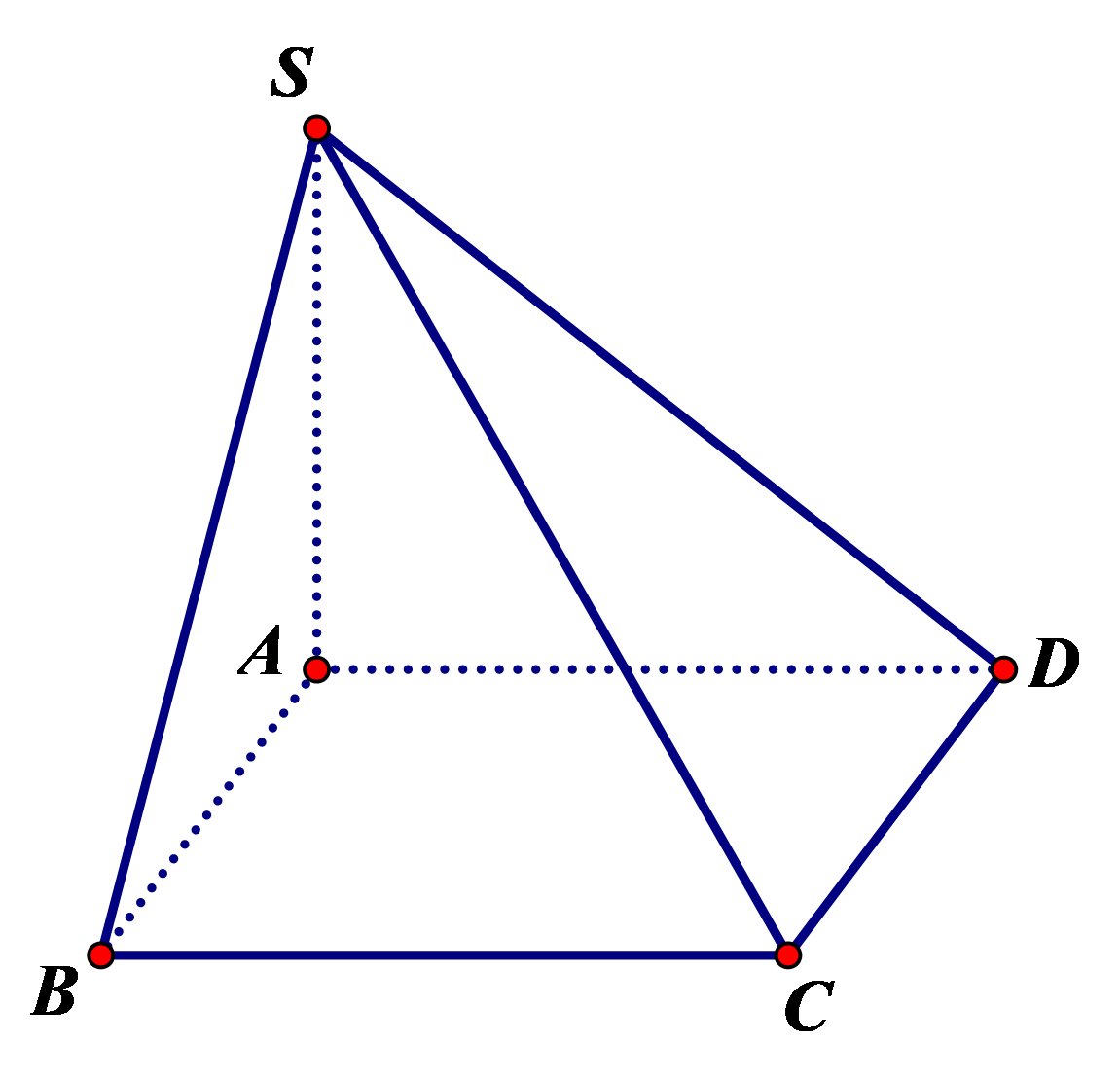
A. a
B.
C.
D.
Số các giá trị nguyên của x thỏa là
A. Vô số
B. 80
C. 17
D. 78
Gọi là hai nghiệm của phương trình và A, B lần lượt là hai điểm biểu diễn hai số phức trong mặt phẳng Oxy. Diện tích của tam giác OAB bằng
A. 6
B. 12
C. 13
D.
Cho hàm số y = f(x) có đạo hàm liên tục trên và thỏa mãn . Diện tích hình phẳng giới hạn bởi các đường: y = f(x), hai trục tọa độ và x = 2 là
A. Đáp án khác.
B.
C.
D.
Một cái ly làm bằng thủy tinh, có hình dạng là khối nón cụt và các kích thước như hình vẽ. Phần rỗng bên trong có thiết diện qua trục là Parabol.
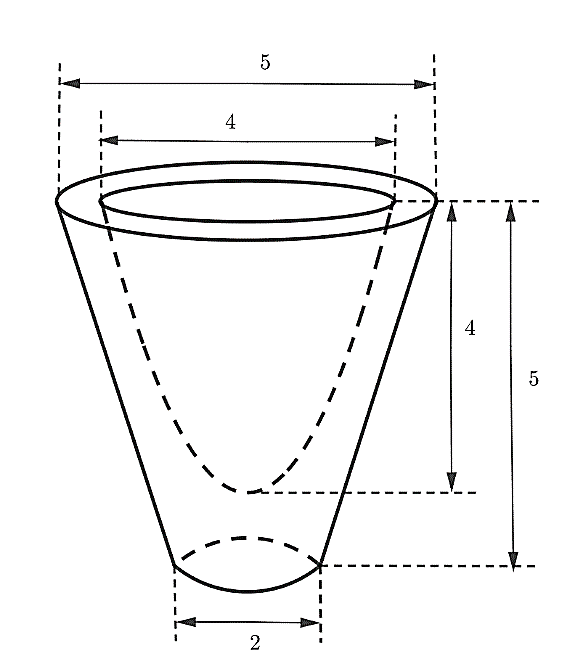
Thể tích khối thủy tinh bằng bao nhiêu?
A.
B.
C.
D.
Trong không gian Oxyz, cho điểm A(0;1;2) và đường thẳng . Gọi (P) là mặt phẳng chứa d và cách A một khoảng lớn nhất. Khoảng cách từ điểm M(5;-1;3) đến (P) bằng
A.
B.
C.
D. 1
Có bao nhiêu giá trị nguyên của tham số để hàm số đồng biến trên khoảng
A. 2017
B. 2019
C. 2018
D. 4
Cho một cổ vật hình trụ có chiều cao đo được là 81 cm, do bị hư hại nên khi tiến hành đo đạc lại thu được AB = 50 cm, BC = 70 cm, CA = 80 cm, với A, B, Cthuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?
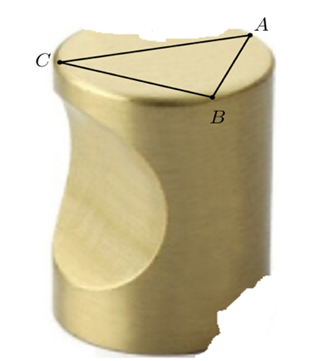
A.
B.
C.
D.
Cho tứ diện ABCD có AB = a, , , . Biết góc giữa hai mặt phẳng (ABD) và (BCD) bằng . Thể tích khối tứ diện ABCD bằng
A.
B.
C.
D.
Trong không gian Oxyz, cho hai điểm A(0;0;10) và . Xét các điểm M thay đổi sao cho tam giác OAM không phải là tam giác nhọn và có diện tích bằng 20. Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?
A. (5;10)
B. (3;5)
C.
D.
Cho các số phức z, w, u thỏa mãn , là số thuần ảo và \. Giá trị nhỏ nhất của thuộc khoảng nào sau đây?
A. (0;5]
B. (5;8)
C. [8;10)
D.
Có bao nhiêu số nguyên dương y để tồn tại số thực x > 1 thỏa mãn
?
A. 16
B. 15
C. 26
D. 27
Cho hàm số . Biết rằng tập hợp tất cả các giá trị thực của tham số m để hàm số có số điểm cực tiểu nhiều nhất là . Giá trị của biểu thức thuộc khoảng nào sau đây?
A. (1;100)
B. (115;130)
C. (100;115)
D. (130;2023)

