Quiz

ĐGTD ĐH Bách khoa - Tư duy Toán học - Hai mặt phẳng vuông góc với nhau

Admin18 câu hỏiĐH Bách KhoaĐánh giá năng lực

18 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Cho hai mặt phẳng (P) và (Q) song song với nhau và một điểm M không thuộc (P) và (Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q)?

A. 2

B. 3

C. 1

D. Vô số

2. Nhiều lựa chọn

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

B. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.

C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

D. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.

3. Nhiều lựa chọn

Cho hình chóp S.ABC có $S A ⊥ (A B C),$ tam giác ABC vuông tại B, kết luận nào sau đây sai?

A. $(S A C) ⊥ (S A B)$

B. $(S A B) ⊥ (A B C)$

C. $(S A C) ⊥ (A B C)$

D. $(S A B) ⊥ (S B C)$

4. Nhiều lựa chọn

Hình lăng trụ đứng có đáy là hình chữ nhật có bao nhiêu mặt là hình chữ nhật ?

A. 4

B. 5

C. 6

D. 3

5. Nhiều lựa chọn

Cho tứ diện SABC có SBC và ABC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác SBC đều, tam giác ABC vuông tại A. Gọi H, I lần lượt là trung điểm của BC và AB. Khẳng định nào sau đây sai?

A. $S H ⊥ A B .$

B. $S H ⊥ A B .$

C. $(S A B) ⊥ (S A C) .$

D. $(S H I) ⊥ (S A B) .$

6. Nhiều lựa chọn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?

(I): $A I ⊥ S C$

$(I I) : (S B C) ⊥ (S A C)$

$(I I I) : A I ⊥ B C$

$(I V) : (A B I) ⊥ (S B C)$

A. 1

B. 2

C. 3

D. 4

7. Nhiều lựa chọn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại BB, SA vuông góc với đáy. Gọi H,K lần lượt là hình chiếu của A trên SB, SC và I là giao điểm của HK với mặt phẳng (ABC). Khẳng định nào sau đây sai?

A. $B C ⊥ A H .$

B. $(A H K) ⊥ (S B C) .$

C. $S C ⊥ A I .$

D. Tam giác IAC đều

8. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy lớn AB; cạnh bên SA vuông góc với đáy. Gọi Q là điểm trên cạnh SA và $Q \neq A, Q \neq S$ ; M là điểm trên đoạn AD và $M \neq A$ . Mặt phẳng (α) qua QM và vuông góc với mặt phẳng (SAD). Thiết diện tạo bởi (α) với hình chóp đã cho là:

A. tam giác.

B. hình thang cân.

C. hình thang vuông.

D. hình bình hành.

9. Nhiều lựa chọn

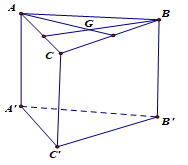
Cho hình lăng trụ tam giác đều ABC.A’B’C’, gọi G là trọng tâm tam giác ABC. (tham khảo hình vẽ). Khẳng định nào sau đây là sai? Media VietJack

A. $A G ⊥ B^{'} C^{'}$

B. $AG ⊥ (B C C^{'} B^{'})$

C. ${AA}^{'} ⊥ (A B C)$

D. $A^{'} G ⊥ (A B C)$

10. Nhiều lựa chọn

Cho tam giác đều ABC cạnh a. Gọi D là điểm đối xứng với A qua BC. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại D lấy điểm S sao cho $S D = \frac{a \sqrt{6}}{2}$ . Gọi I là trung điểm BC; kẻ IH vuông góc SA $(H \in S A) .$ Khẳng định nào sau đây sai?

A. $S A ⊥ B H .$

B. $(S D B) ⊥ (S D C) .$

C. $(S A B) ⊥ (S A C) .$

D. $B H ⊥ H C .$

11. Nhiều lựa chọn

Cho hình chóp đều S.ABC. Mặt phẳng (α) qua A, song song với BC và vuông góc với mặt phẳng (SBC). Thiết diện tạo bởi (α) với hình chóp đã cho là:

A. tam giác đều

B. tam giác cân

C. tam giác vuông

D. tứ giác

12. Nhiều lựa chọn

Cho hình chóp đều S.ABCD. Mặt phẳng $(α)$ qua AB và vuông góc với mặt phẳng (SCD). Thiết diện tạo bởi $(α)$ với hình chóp đã cho là:

A. tam giác cân

B. hình bình hành

C. hình thang vuông

D. hình thang cân

13. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, $A B = 2 a, A D = D C = a$ ; cạnh bên SA=a và vuông góc với đáy. Mặt phẳng (α) qua SD và vuông góc với mặt phẳng (SAC). Tính diện tích S của thiết diện tạo bởi (α) với hình chóp đã cho.

A. $S = \frac{a^{2}}{2} .$

B. $S = \frac{a^{2} \sqrt{2}}{2} .$

C. $S = \frac{a^{2} \sqrt{3}}{2} .$

D. $S = \frac{a^{2}}{4} .$

14. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O với AB=a, AD=2a. Cạnh bên SA=a và vuông góc với đáy. Gọi $(α)$ là mặt phẳng qua SO và vuông góc với (SAD). Tính diện tích S của thiết diện tạo bởi $(α)$ và hình chóp đã cho.

A. $S = \frac{a^{2} \sqrt{3}}{2} .$

B. $S = \frac{a^{2} \sqrt{2}}{2} .$

C. $S = \frac{a^{2}}{2} .$

D. $S = a^{2} .$

15. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng $30^{°}$ . Tính diện tích hình chữ nhật ABCD.

A. $S_{A B C D} = a^{2} .$

B. $S_{A B C D} = \sqrt{2} a^{2} .$

C. $S_{A B C D} = \sqrt{3} a^{2} .$

D. $S_{A B C D} = 2 a^{2} .$

16. Nhiều lựa chọn

Cho hình chóp tam giác đều S.ABC đỉnh S, có độ dài cạnh đáy bằng a và cạnh bên bằng $\frac{a \sqrt{3}}{2}$ . Gọi M và N lần lượt là trung điểm của các cạnh SB và SC. Tính theo a diện tích tam giác AMN, biết rằng mặt phẳng (AMN) vuông góc với mặt phẳng (SBC).

A. $S_{Δ A M N} = \frac{a^{2} \sqrt{10}}{4} .$

B. $S_{Δ A M N} = \frac{a^{2} \sqrt{10}}{8} .$

C. $S_{Δ A M N} = \frac{a^{2} \sqrt{10}}{12} .$

D. $S_{Δ A M N} = \frac{a^{2} \sqrt{10}}{16} .$

17. Nhiều lựa chọn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=a.. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Đường thẳng BC tạo với mặt phẳng (SAC) góc 30⁰. Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = \frac{a^{2} \sqrt{2}}{2} .$

B. $S_{Δ A B C} = a^{2} \sqrt{2} .$

C. $S_{Δ A B C} = \frac{a^{2} \sqrt{2}}{4} .$

D. $S_{Δ A B C} = \frac{a^{2} \sqrt{2}}{6} .$

18. Nhiều lựa chọn

Cho hình chóp S.ABC có đáy $\hat{B A C} = 90^{0}, B C = 2 a, \hat{A C B} = 30^{0}$ . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC). Biết rằng tam giác SAB cân tại S và tam giác SBC vuông tại S. Tính diện tích tam giác SAB.