Đề thi thử TS vào 10 (Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Yên Hòa_Quận Cầu Giấy
13 câu hỏi
1) Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\).
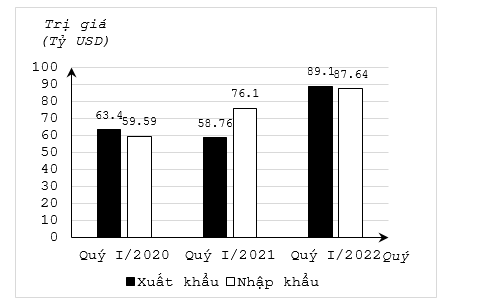
a) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) là bao nhiêu tỷ USD?
b) Trị giá xuất khẩu trong quý I/2021 chiếm bao nhiêu phần trăm so với tổng trị trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) (làm tròn đến hàng đơn vị).
2) Một hộp có \(25\) chiếc thẻ cùng loại, mỗi thẻ được ghi đúng trong các số \(1;2;3;4;...;25,\) hai thẻ khác nhau ghi hai số khác nhau. Xét phép thử “Rút ngẫu nhiên một thẻ trong hộp” và biến cố N: “Số xuất hiện trên thẻ được rút ra là một số chia hết cho \(5\)”. Tính xác suất biến cố N.
1) Tính giá trị của A biểu thức khi x=16.
2) Rút gọn B.
3) Tìm các giá trị của x sao cho .
1)Nếu hai vòi nước cùng chảy vào một bể (không chứa nước) thì sau \[1\] giờ \[20\] phút đầy bể. Nếu mở vòi thứ nhất chảy trong \[10\] phút rồi khóa lại, vòi thứ hai chảy tiếp trong \[12\] phút thì được \(\frac{2}{{15}}\) bể. Hỏi nếu mỗi vòi chảy riêng thì sau bao lâu sẽ đầy bể?
2) Một mảnh đất hình chữ nhật có chu vi bằng \[82\,\,{\rm{m}}{\rm{.}}\] Nếu tăng chiều dài thêm \[5\,{\rm{m}}\] và gấp đôi chiều rộng thì diện tích mảnh đất tăng thêm \[560\,{{\rm{m}}^2}.\] Tính kích thước ban đầu của mảnh đất hình chữ nhật.
3) Cho phương trình bậc hai: \({x^2}\; - \;2\left( {m - 2} \right)x\; - \;6m\; + \;3\; = \;0\). Tìm \[m\] để phương trình có hai nghiệm phân biệt.
1) Cùng với cây đa, sân đình, từ bao đời nay, giếng làng đã trở thành một trong những biểu tượng vẻ đẹp của vùng quê Việt Nam, đặc biệt là ở đồng bằng Bắc Bộ. Giếng làng chính là nơi chứng kiến bao sự kiện của làng xóm từ thế hệ này qua thế hệ khác. Hiện nay, tại làng Trung Kính Thượng, phường Trung Hòa vẫn đang lưu giữ một chiếc giếng cổ (Hình 1). Biết nắp giếng có dạng hình tròn với bán kính \[55\,{\rm{cm}}\], miệng giếng là hình vành khăn có độ dày \[{\rm{10}}\,{\rm{cm}}\] (Hình 2).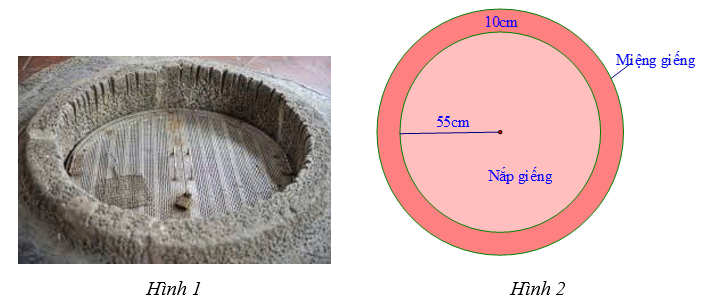
a) Tính diện tích phần nắp giếng có dạng hình tròn (được chú thích như Hình 2).
b) Tính diện tích phần miệng giếng hình vành khăn (phần tô đậm trên Hình 2).(Lấy \(\pi \approx 3,14).\)
a) Chứng minh tứ giác \[BCEF\] nội tiếp.
b) Đường thẳng \[AM\] cắt đường tròn \[\left( O \right)\] tại điểm thứ hai là \[D.\] Chứng minh \(OM \bot BC\) và \(M{B^2} = MA \cdot MD.\)
c) Kẻ đường kính \(AK\) của \(\left( O \right).\) Chứng minh \(OM = \frac{1}{2}AH.\)
(0,5 điểm) Cho tam giác đều có độ dài cạnh bằng Bạn Nam cắt một hình chữ nhật sao cho thuộc lần lượt thuộc Đặt cạnh Tìm để diện tích hình chữ nhật lớn nhất.