Đề thi thử TS vào 10 (Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Xuân La_Quận Tây Hồ_TP. Hà Nội

2) Một hộp có A chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số $1;2;3;4;\mathrm{...};20;$ hai thẻ khác nhau thì ghi hai số khác nhau. Xét phép thử “Rút một thẻ trong chiếc hộp” và biến cố A: “Số xuất hiện trên thẻ là số chia hết cho 3”. Tính xác suất của biến cố A

1) Tính giá trị của A biểu thức  khi x=1.

2) Chứng minh $\mathrm{B}=\frac{2}{\sqrt{\mathrm{x}}+2}$.

3) Tìm giá trị của $\mathrm{x}$ để biểu thức A+B đạt giá trị nguyên nhỏ nhất.

1) Năm ngoái, hai công ty kinh doanh bán được \(7200\) sản phẩm. Năm nay, công ty thứ nhất bán được số sản phẩm vượt mức \(15\% \), công ty thứ hai bán được số sản phẩm vượt mức \(12\% \) so với năm ngoái. Do đó năm nay, cả hai công ty bán được \(8190\) sản phẩm. Hỏi năm ngoái, mỗi công ty đã bán được bao nhiêu sản phẩm?

2) Một ô tô và một xe máy cùng khởi hành từ địa điểm \[A\] và đi đến địa điểm \[B\]. Do vận tốc của xe ô tô lớn hơn vận tốc của xe máy là \(10\,{\rm{km/h}}\) nên ô tô đến \[B\] sớm hơn xe máy \(36\) phút. Biết quãng đường \[AB\] dài \(120\,{\rm{km}}{\rm{.}}\) Tính vận tốc của mỗi xe (giả định rằng vận tốc của mỗi xe là không đổi trên toàn bộ quãng đường \[AB).\]

Giải bất phương trình sau: $\frac{2\mathrm{x}-1}{5}-\frac{\mathrm{x}}{2}\ge \mathrm{x}-1$

1)Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn có đường kính \(AB = 1,2{\rm{\;m}}\) (lấy \(\pi \approx 3,14\) và kết quả làm tròn đến chữ số thập phân thứ hai). 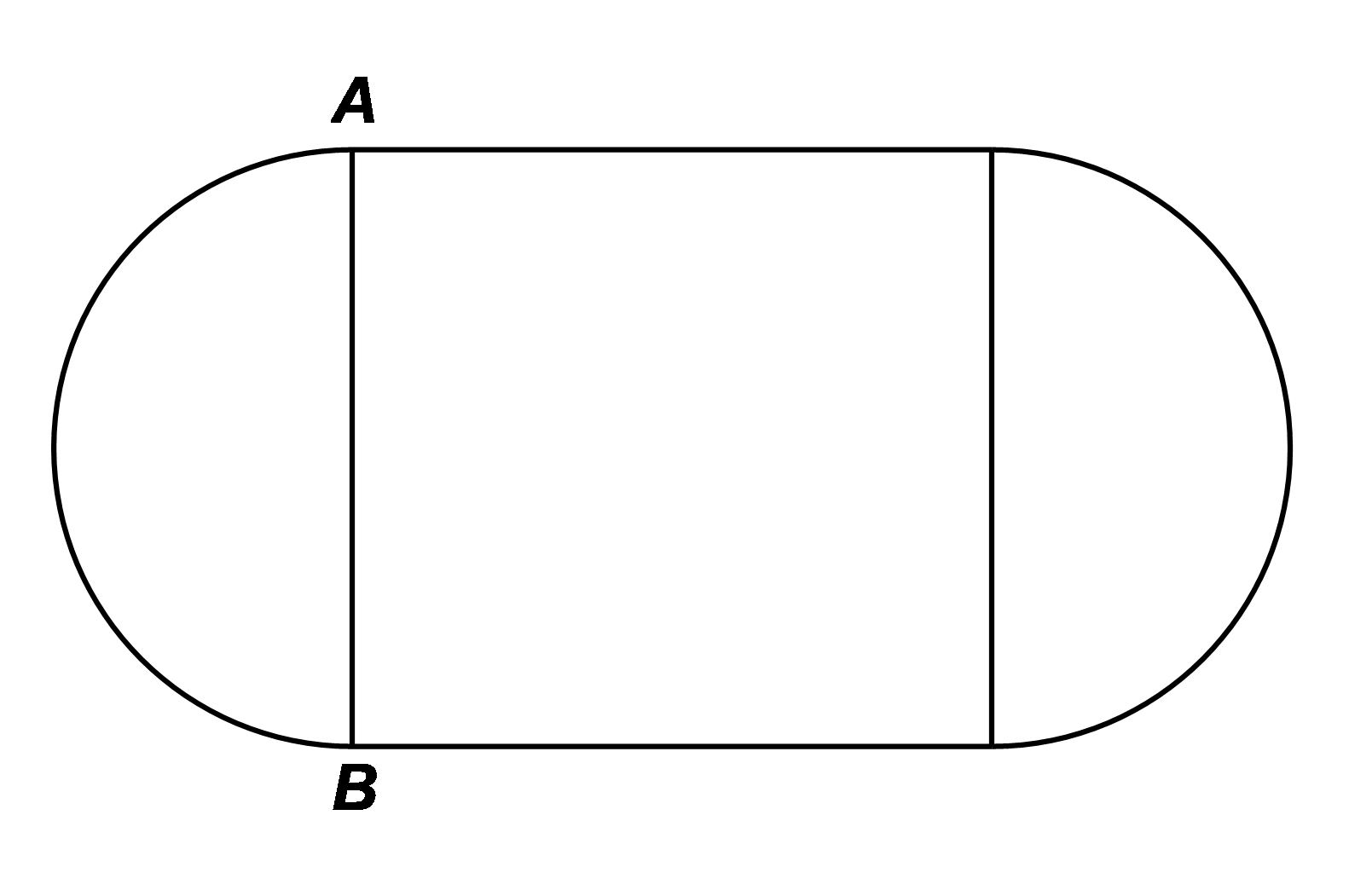a) Tính diện tích mặt bàn. b) Người ta muốn nới rộng mặt bàn bằng cách ghép thêm vào giữa một hình chữ nhật có một kích thước là \(AB\) (như hình vẽ). Hỏi kích thước còn lại của hình chữ nhật là bao nhiêu để diện tích mặt bàn tăng gấp ba lần sau khi nới?

a) Chứng minh tứ giác \(ABDE\) nội tiếp.  

b) Kẻ $OM$ vuông góc với $BC$ tại $M.$ Đường thẳng $OM$ cắt $AB,AC$ theo thứ tự tại $P,Q$. Gọi $N$ là trung điểm của $PQ.$ Chứng minh $\widehat{APQ}=\widehat{BED}$ và $AP\cdot CM=PN\cdot HC.$

c) Gọi \(I\) là giao điểm của tia \(MH\) với đường tròn \(\left( O \right).\) Chứng minh ba điểm \(I,\,A,\,N\) thẳng hàng.

(0,5 điểm) Gia đình nhà bạn An muốn làm một bể cá cảnh có dạng hình hộp chữ nhật không nắp, đáy là hình chữ nhật có chiều dài gấp đôi chiều rộng và có thể tích bằng \[1\,{{\rm{m}}^3}\]. Biết rằng chi phí để làm mặt đáy là \[500\,\,000\] đồng\[{\rm{/}}{{\rm{m}}^2}\] và đắt gấp đôi chi phí làm các mặt xung quanh. Em hãy tính xem, gia đình bạn An cần chi tối thiểu bao nhiêu tiền để làm bể cá nói trên (kết quả làm tròn đến hàng nghìn)?