Đề thi thử TS vào 10 (Tháng 1) năm học 2025 - 2026_Môn Toán_THCS Cầu Giấy_Quận Cầu Giấy
13 câu hỏi
(1,5 điểm)
1) Biểu đồ sau cho biết số lượng các loại ô tô một cửa hàng bán được trong năm 2023:
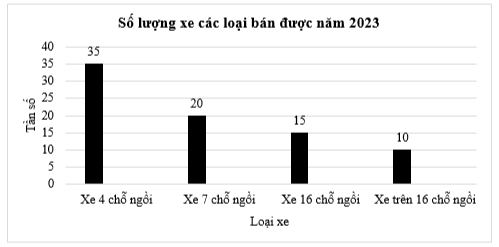
a) Lập bảng tần số cho dữ liệu được biểu diễn trên biểu đồ.
b) Giả sử tỉ lệ các loại xe bán được không đổi và cửa hàng bán được tổng số 240 ô tô các loại trong năm 2023. Hãy ước lượng số ô tô 4 chỗ cửa hàng bán được.
2) Gieo một con xúc xắc đồng chất 100 lần và ghi lại kết quả trong bảng sau:

Xét biến cố A “Số chấm xuất hiện trên mặt xúc xắc là số lẻ chia hết cho A”. Tính xác suất của biến cố A
1) Tính giá trị của biểu thức A khi x=4
2) Rút gọn biểu thức B.
3) Tìm giá trị của x để biểu thức đạt giá trị lớn nhất.
(2,5 điểm)
1) Trong kỳ thi môn toán lớp 9, một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát cho. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 42 tờ giấy thi. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 1 tờ giấy thi, bao nhiêu thí sinh làm bài 2 tờ giấy thi? Biết rằng có 3 thí sinh làm 3 tờ giấy thi.
2)Theo kế hoạch, một xưởng may phải may xong 360 bộ quần áo trong một thời gian quy định. Đến khi thực hiện, mỗi ngày xưởng đã may được nhiều hơn 4 bộ quần áo so với số bộ quần áo phải may trong một ngày theo kế hoạch. Vì thế xưởng đã hoàn thành kế hoạch trước 1 ngày. Hỏi theo kế hoạch, mỗi ngày xưởng phải may bao nhiêu bộ quần áo?
(2,5 điểm)3)Cho đường thẳng . Tìm m để (d) cắt Ox tại A, cắt Oy tại B mà .
(4,0 điểm)
1) Cho tam giác ABC đều có cạnh AB = 3cm nội tiếp đường tròn tâm O bán kính R. Hạ AH vuông góc với BC. Tính diện tích phần nằm trong hình tròn (O;R) và nằm ngoài tam giác ABC (phần tô đậm trong hình bên).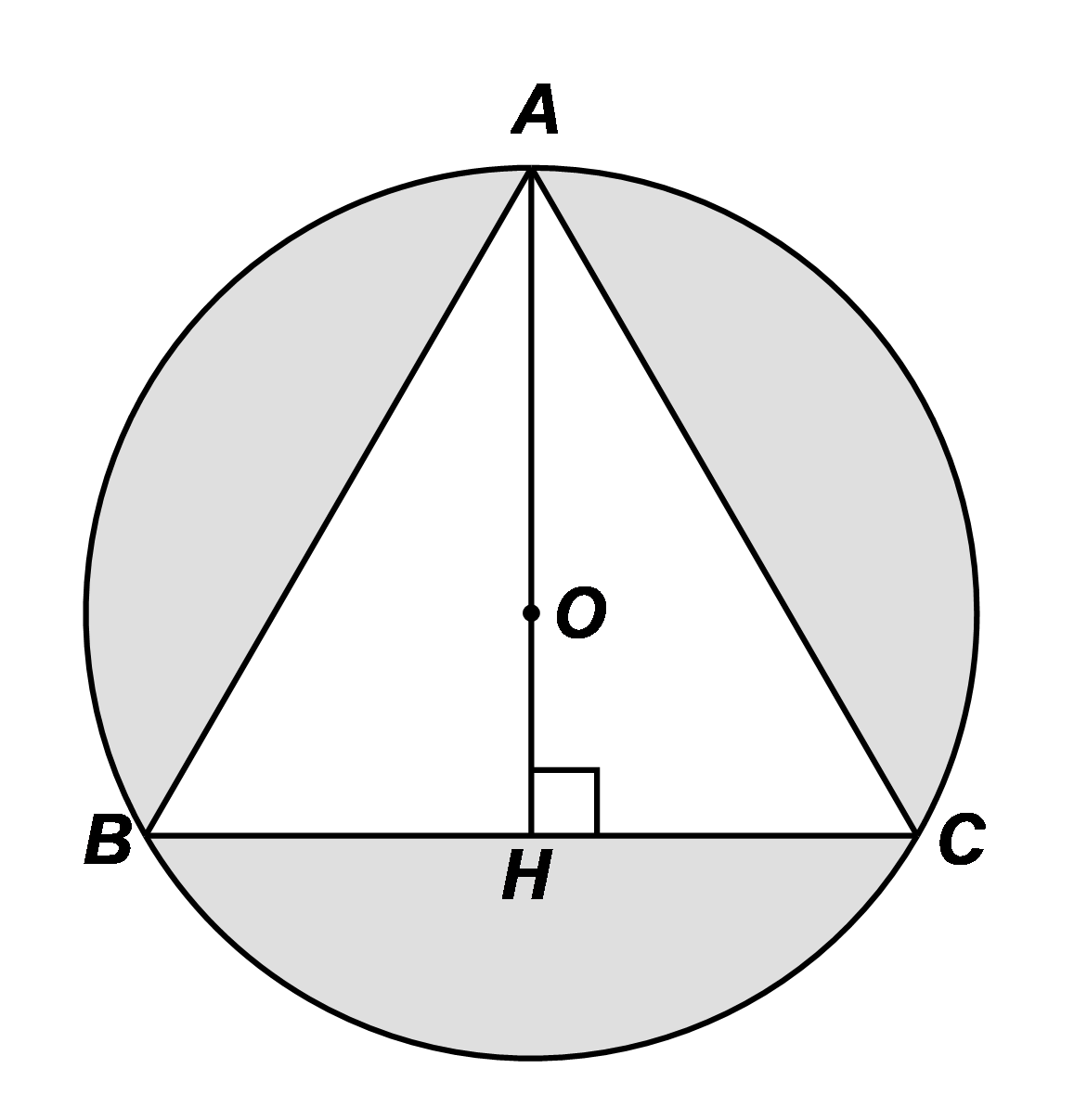
a) Chứng minh rằng bốn điểm cùng thuộc một đường tròn.
b) Chứng minh rằng đồng dạng với .
c) Chứng minh rằng .
d) Kẻ phân giác góc \(AMB\) cắt \(AB\) tại \(P\). Tìm vị trí của \(M\) thỏa mãn đề bài để \(\frac{{MP}}{{MA + MB}}\) đạt giá trị lớn nhất.
(0,5 điểm) Trong một xưởng cơ khí đang có sẵn những thanh thép dài \(7,4\,\,{\rm{m}}{\rm{.}}\) Một công trình xây dựng đang cần có \(1\,\,000\) đoạn thép dài \(0,7\,\,{\rm{m}}\) và \(2\,\,000\) đoạn thép dài \(0,5\,\,{\rm{m}}\) (cùng kích cỡ với thép \(7,4\,\,{\rm{m)}}{\rm{.}}\) Em hãy tìm xem cần dùng bao nhiêu thanh thép \(7,4\,\,{\rm{m}}\) để thoả mãn yêu cần trên với chi phí tiết kiệm nhất.








