49 câu hỏi
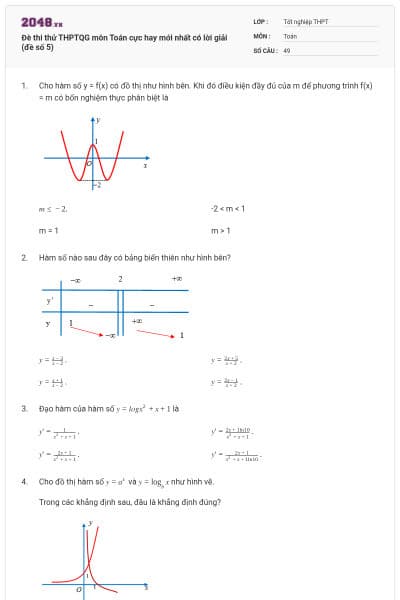
Cho hàm số y = f(x) có đồ thị như hình bên. Khi đó điều kiện đầy đủ của m để phương trình f(x) = m có bốn nghiệm thực phân biệt là

-2 < m < 1
m = 1
m > 1
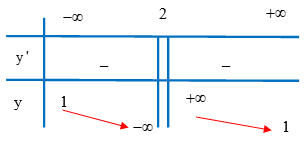
Hàm số nào sau đây có bảng biến thiên như hình bên?
Đạo hàm của hàm số là
Cho đồ thị hàm số và như hình vẽ.
Trong các khẳng định sau, đâu là khẳng định đúng?

a > 1 và b > 1
0 < b < 1 < a
0 < a < 1 < b
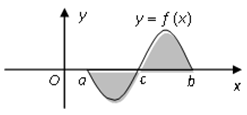
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, đường thẳng x = a, x = b(như hình bên).
Hỏi cách tính S nào dưới đây đúng?
Cho số phức . Khi đó tổng thực và phần ảo của số phức là
-5
2
-7
9
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, , và SA vuông góc với đáy (ABCD). Thể tích V của khối chớp S.ABCD bằng
Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có tâm I(1;-2;0)và đi qua điểm A(-1;0;3). Khi đó (S) có bán kính R bằng
R = 17
R = 13
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng . Điểm nào sau đây thuộc đường thẳng ?
Trong các hàm số sau, hàm số nào là hàm số chẵn?
y = sinx.
y = cosx.
y = tanx.
y = cotx.
Có 8 tem thư khác nhau và 5 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư và 3 bì thư sau đó mỗi tem thư dán vào 1 bì thư. Hỏi có bao nhiêu cách dán.
1120
3630
2110
3360
Khẳng định nào sau đây đúng?
Hàm số có ba điểm cực trị.
Hàm số có hai điểm cực trị.
Hàm số có một điểm cực trị.
Hàm số có hai điểm cực trị.
Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1 có hệ số góc là
-1
1
-2
2
Giá trị nhỏ nhất của hàm số trên đoạn [-1;2] là
-4
2
-1
23
Tập nghiệm S của bất phương trình là
Cho a,b là các số thực dương thỏa mãn . Khẳng định nào sau đây sai?
Tập xác định D của hàm số là
D = R
Họ nguyên hàm của hàm số là
Cho tích phần , đặt Khẳng định nào sau đây đúng?
Biết lần lượt là hai điểm biểu diễn số phức trên mặt phẳng tọa độ phức Oxy. Khi đó môđun của số phức bằng
Cho hình chóp S.ABC có ABC là tam giác đều cạnh a và SA vuông góc với đáy. Góc tạo bởi mặt phẳng (SBC) và mặt phẳng (ABC) bằng 30º. Khi đó thể tích của khối chóp S.ABC được tính theo a là:
Số mặt phẳng đối xứng của hình lập phương là
3
6
9
12
Cho hình trụ có bán kình đáy 3cm, chiều cao 4cm. Khi đó diện tích toàn phần của hình trụ là
Trong không gian với hệ tọa độ Oxzy, cho đường thẳng và mặt phẳng . Phương trình mặt phẳng đi qua O song song với và vuông góc với mặt phẳng (P) là
Trong mặt phẳng Oxy cho đường tròn . Hỏi trong bốn đường tròn đường tròn nào là ảnh của (C) qua phép tịnh tiến.
Cho a,b là các số thực khác 0. Nếu thì bằng bao nhiêu?
T = -2018.
T = -2017
T = 2017
T = 2019
Gọi S là tập hợp các giá trị thực của tham số m làm cho hàm số đồng biến trên khoảng (2;3). Khi đó tập S là
Tất cả các giá trị thực của tham số m để đồ thị hàm số có ba tiệm cận là
Tìm tất cả các giá trị thực của tham số m để phương trình có ba nghiệm thực phân biệt?
m = 2
2 < m < 3
m = 3
không tồn tại m
Đặt . Biểu thức biểu diễn theo a,b,c chính xác là
Một giáo viên sau 10 năm tích góp được số tiền 100 triệu đồng và quyết định gửi vào ngân hàng với lãi suất 7.5% một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ nhập vào vốn ban đầu. Nếu lãi suất không thay đổi thì tối thiểu sau bao nhiêu năm thì giáo viên đó có được số tiền 165 triệu đồng (tính cả gốc lẫn lãi)?
5 năm.
6 năm.
7 năm.
8 năm.
Diện tích hình phẳng giới hạn bởi các đường
4
1
Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường quanh trục Ox có kết quả viết dưới dạng (a, b nguyên tố cùng nhau). Khi đó a + b bằng
11
17
31
2
Cho số phức z, biết . Khi đó số phức z có phần ảo bằng bao nhiêu?
-1
-2
1
2
Cho x,y là các số phức ta có các khẳng định sau:
1) là hai số phức liên hợp của nhau.
2) là hai số phức liên hợp của nhau.
3) là hai số phức liên hợp của nhau.
Hỏi có bao nhiêu khẳng định đúng
không
một
hai
ba
Cho hình hộp có thể tích bằng V. Cho E, F lần lượt là trung điểm của DD' và CC'. Khi đó ta có tỉ số bằng
1
Một hình nón có bán kính đáy r = a, chiều cao . Diện tích xung quanh của hình nón được tính theo a là
2
3
4
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt phẳng . Biết , khi đó m,n có giá trị bao nhiêu?
Có bao nhiêu giá trị nguyên của a để phương trình có nghiệm thuộc khoảng .
0
1
2
3
Có 5 đoạn thẳng có độ dài lần lượt là 1cm, 2cm, 3cm, 4cm, 5cm. Lấy ngẫu nhiên ra 3 đoạn thẳng, tính xác suất để 3 đoạn thẳng được chọn ra là độ dài 3 cạnh của 1 tam giác.
Trong không gian với hệ tọa độ Oxyz, cho vecto cùng phương với vecto . Biết vecto tạo với tia Oy một góc nhọn và . Khi đó tổng bằng bao nhiêu?
Cho đường thẳng cắt đồ thị tại hai điểm phân biệt A, B. Biết là giá trị làm cho độ dài đoạn AB nhỏ nhất. Khi đó giá trị nào sau đây gần nhất?
0
-2
3
-4
Biết số phức là hai nghiệm của phương trình (b,c là các số thực). Khi đó môdun của số phức là
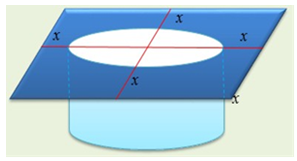
Trên một mảnh đất hình vuông có diện tích người ta đào một cái ao nuôi cá hình trụ có 2 đáy là hình tròn (như hình vẽ) sao cho tâm của hình tròn trùng với tâm của mảnh đất. Ở giữa mép ao và mép mảnh đất người ta để lại một khoảng đất trống để đi lại, biết khoảng cách nhỏ nhất giữa mép ao và mép mảnh đất là x(m). Thể tích V của ao lớn nhất có thể là? (Giả sử chiều sâu của ao cũng là x(m))
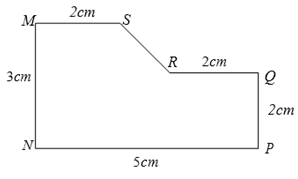
Cho hình phẳng (H) như hình vẽ.
Khi quay hình phẳng (H) quanh cạnh MN ta được một vật thể tròn xoay. Hỏi thể tích V của vật thể tròn xoay được tạo ra là
Một máy bơm nước có ống nước đường kính 50 cm, biết tốc độ dòng chảy trong ống là 0,5m/ s. Hỏi trong 1 giờ máy bơm đó bơm được bao nhiêu nước (giả sử nước lúc nào cũng đầy ống)?
Trong mặt phẳng (α) cho hình vuông ABCD cạnh a. Các tia Bx và Dy vuông góc với mặt phẳng (α) và cùng chiều. Các điểm M và N lần lượt thay đổi trên Bx, Dy sao cho mặt phẳng (MAC) và (NAC) vuông góc với nhau. Khi đó tích BM.DN bằng
Gọi là hệ số của số hạng chứa trong khai triển nhị thức Niutơn với ; n là số nguyên dương thỏa mãn . Tìm
2017
2019
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng . Đường vuông góc chung của đi qua điểm nào sau đây?
N(1;-1;-4)
P(2;0;1)
Q(0;-2;-5)