50 câu hỏi
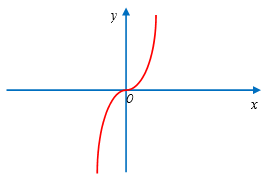
Đường cong trong hình bên là đồ thị của một hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
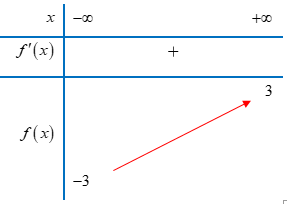
Cho hàm số y = f(x) có bảng biến thiên như hình bên. Số đường tiệm cận ngang của đồ thị hàm số y = f(x) là
0
1
2
3
Cho hàm số . Khi đó giá trị là
-2
-1
1
2
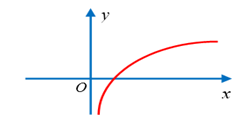
Hàm số nào trong các hàm số dưới đây có đồ thị hợp với hình vẽ bên?
Trong các đẳng thức sau, đẳng thức nào đúng?
Cho số phức . Môdun của z được tính theo công thức nào sau đây?
|z| = a + b
Cho hình trụ có bán kính đường tròn đáy bằng chiều cao và bằng 2cm. Diện tích xung quanh của hình trụ bằng
2
4
8
Trong không gian với hệ tọa độ Oxyz, cho điểm . Hình chiếu vuông góc của M trên trục Oz là điểm M'. Khi đó tọa độ điểm M' là
Cho dãy số thỏa mãn với và . Tổng của 10 số hạng đầu tiên của dãy số bằng bao nhiêu?
177146.
19682.
59048.
155.
Tất cả các giá trị thực của tham số m để đồ thị hàm số có tiệm cận đứng nằm bên phải trục Oy là
m > 0
m < 0
m > 0 và
m < 0 và
Gọi S là tập các giá trị m thỏa mãn hàm số chỉ có đúng một cực trị. Khi đó tập S là
S = [0;1)
Cho lăng trụ đều có cạnh đáy bằng a, chiều cao bằng 2a. Tính cosin của góc tạo bởi hai đường thẳng AC và BC'.
Tính tổng tất cả các nghiệm của phương trình trên đoạn .
Gọi D là tập xác định của hàm số . Khi đó tập D là
D = (0;2)
D = (1;2)
Nếu F(x) là một nguyên hàm của hàm số và đồ thị đi qua điểm thì F(x) là
Cho tích phân . Biết kết quả với . Khi đó a - b + c bằng bao nhiêu?
-
2
-2
Cho a, b là các số thực dương thỏa mãn . Tích phân có giá trị bằng bao nhiêu?
I = 0
I = 1
I = |a-b|
I = e
Trong các số từ 100 đến 999 có bao nhiêu số mà các chữ số của nó tăng dần hoặc giảm dần?
1224
204
240
168
Số phức z thỏa mãn . Khi đó điểm nào dưới đây là điểm biểu diễn số phức z trong mặt phẳng phức Oxy?
M(2;-3)
N(-2;3)
P(-2;-3)
Q(2;3)
Biết là số thực và là số ảo thỏa mãn . Khi đó có tổng phần thực và phần ảo là:
-64
0
-8
-32
Một lăng trụ đứng có đáy là tam giác đều cạnh a, cạnh bên bằng b. Khi đó thể tích V của khối lăng trụ đó là
Cho hình nón có chiều cao bằng 6 cm, góc giữa trục và đường sinh bằng . Thể tích của khối nón là
Trong không gian với trục tọa độ Oxyz, cho . Khi đó diện tích tam giác ABC bằng bao nhiêu?
Trong không gian với trục tọa độ Oxyz, cho mặt cầu . Mặt cầu (S') đồng tâm với mặt cầu (S') (có tâm trùng với tâm mặt cầu (S)) và đi qua điểm . Khi đó, bán kính R của mặt cầu (S')bằng bao nhiêu?
R = 4
R = 3
Đường thẳng nối hai điểm cực đại và cực tiểu của đồ thị hàm số đi qua điểm M(2;-1) khi m bằng
2
-2
-3
3
Hàm số có tập giá trị là
[-1;1]
[0;1]
Tập hợp các giá trị thực của m để đồ thị hàm số có đúng một đường tiệm cận là
{0}
Cho hàm số có đồ thị . Gọi A, B, C là ba điểm cực trị của (C) và là giá trị thỏa mãn A, B, C đều thuộc các trục tọa độ, khi đó gần giá trị nào nhất trong các giá trị sau?
-1
-3
4
5
Cho a là số thực dương khác 1. Xét hai số thực . Phát biểu nào sau đây đúng?
Cho x, y là các số thực thỏa mãn Khi đó tỉ số bằng bao nhiêu?
2
Cho a, b, c là các số thực thỏa mãn . Giá trị của biểu thức bằng bao nhiêu?
T = 3
T = 2
T = 1
T = 0
Cho a, b là các số thực và hàm số liên tục tại x = 2. Tính giá trị của biểu thức T = a+b.
T = 5
T = 3
Cho hình phẳng (H) giới hạn bởi các đường . Khi đó thể tích V của khối tròn xoay tạo ra khi quay (H) quay quanh trục Ox bằng bao nhiêu?
Có bao nhiêu số phức z thỏa mãn điều kiện và |z| = 2?
1
2
3
4
Tập hợp các điểm trong mặt phức biểu diễn số phức z thỏa mãn là một đường thẳng có phương trình
Một hình trụ có bán kính đáy bằng 1, thiết diện qua trục là hình vuông. Thể tích của khối cầu ngoại tiếp hình trụ là
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết thể tích khối chóp S.ABCD bằng . Độ dài cạnh bên SA bằng bao nhiêu?
Cho hình lập phương cạnh a. Xét tứ diện AB'CD'. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được.
Từ 4 bạn Tùng, Tuấn, Tiến, Tú cần chọn ra 3 bạn vào các chức vụ lớp trưởng, lớp phó học tập và bí thư lớp. Tính xác suất để sau khi chọn thì bạn Tùng không được phép làm lớp trưởng, chức lớp phó học tập phải là bạn Tiến hoặc bạn Tú.
Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng . Đường thẳng đi qua M(0;1;1) vuông góc với và cắt có phương trình là?
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng và đường thẳng Biết đường thẳng nằm trong mặt phẳng (P). Tổng m + n gần giá trị nào nhất sau đây?
3
4
5
6
Cho các số thực a, b, c thỏa mãn . Số giao điểm của đồ thị hàm số và trục hoành là
0
1
2
3
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của hình hộp chữ nhật và hình trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau?

8,3 cm
8,4 cm
8,5 cm
8,6 cm
Có bao nhiêu giá trị nguyên m để bất phương trình nghiệm đúng với ?
0
1
2
Vô số
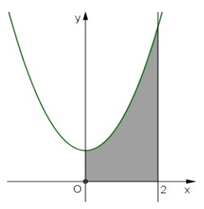
Miền hình phẳng trong hình vẽ được giới hạn bởi đường cong , trục hoành, trục tung và đường thẳng x = 1=. Biết thì diện tích hình phẳng đó đạt giá trị nhỏ nhất. Giá trị gần giá trị nào nhất trong các giá trị sau?
0
1
4
-3
Có bao nhiêu số nguyên dương m không vượt quá 2018 thỏa mãn là số thuần ảo?
504.
505.
2017.
2018.
Cho số nguyên . Giả sử ta có khai triển
. Biết rằng tổng Tính
Có một bình chứa 100 tấm thẻ đánh số từ 1 đến 100. Chọn ngẫu nhiên một tấm thẻ. Gọi a là số ghi trên tấm thẻ và x là chữ số tần cùng của số . Tính xác suất để x là số chia hết cho 4.
Trong không gian với hệ trục tọa độ Oxyz, cho . Tìm tọa độ điểm M thuộc mặt phẳng Oxy sao cho tổng đạt giá trị nhỏ nhất.
M(2;1;0)
M(1;2;0)
M(-2;1;0)
M(1;-2;0)
Cho hình lập phương có . Gọi là mặt phẳng chứa đường thẳng CD' và tạo với mặt phẳng (BB'D'D) góc nhỏ nhất. Cho . Tìm giá trị nguyên âm lớn nhất của T biết a là số nguyên.
-1
-2
-6
-4