149 câu hỏi
Giá trị nhỏ nhất của hàm số trên đoạn bằng:
3
2
-1
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Tính giá trị
Tìm giá trị nhỏ nhất của hàm số trên đoạn
1
-2
0
-5
Xét hàm số trên . Khẳng định nào sau đây đúng
Giá trị lớn nhất của hàm số trên đoạn bằng
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm và có một vecto pháp tuyến . Phương trình của (P) là
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng qua A(1;2;-1) có một vecto pháp tuyến có phương tình là
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(0;1;2), B(2;-2;1), C(-2;0;1). Phương trình mặt phẳng đi qua A và vuông góc với BC là:
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm . Phương trình nào sau đây là phương trình của mặt phẳng đi qua A và vuông góc BC
Cho hàm số . Khẳng định nào sau đây đúng?
Đồ thị hàm số có điểm cực đại là A(1; -1)
Đồ thị hàm số có điểm cực tiểu là A(1;-1)
Đồ thị hàm số có điểm cực tiểu là B(-1; 3)
Đồ thị hàm số có điểm cực tiểu là C(1; 1)
Với x là số thực dương khác 1, biểu thức bằng
Cho a là số thực dương khác 1, biểu thức bằng
Cho a là số dương khác 1, biểu thức bằng:
Cho a là số thực dương khác 1, biểu thức bằng
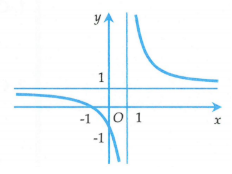
Đồ thị hàm số nào dưới đây có tiệm cận đứng?
Đồ thị hàm số nào dưới đây có tiệm cận ngang?
Đồ thị hàm số nào dưới đây có tiệm cận đứng?
Đồ thị hàm số nào dưới đây có tiệm cận đứng và tiệm cận ngang ?
Trong không gian với hệ tọa độ Oxyz, cho hai điểm . MẶt cầu (S) đường kính AB có phương trình là
Trong không gian với hệ tọa độ Oxyz, viết phương trình chính tắc của mặt cầu có đường kính AB với là
Trong không gian với hệ tọa độ Oxy, cho hai điểm . Mặt cầu nhận AB làm đường kính có phương trình là
Hàm số nghịch biến trên khoảng nào?
Cho hàm số . Mệnh đề nào sau đây đúng
Hàm số đồng biến trên khoảng
Hàm số nghịch biến trên R
Hàm số đồng biến trên R
Hàm số đồng biến trên khoảng và
Cho hàm số . Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên khoảng
Hàm số nghịch biến trên khoảng
Hàm số nghịch biến trên khoảng
Hàm số đồng biến trên khoảng
Cho hàm số . Mệnh đề nào dưới đây đúng?
Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
Hàm số đồng biến trên khoảng
Hàm số nghịch biến trên khoảng và đồng biến trên khoảng
Hàm số nghịch biến trên khoảng
Tập xác định của hàm số là
(1;2)
Tập xác định của hàm số là
D = R\{3}
D = R
Tập xác định của hàm số là
R\{1}
R
Hàm số có tập xác định là:
R
Hàm số có tập xác định là
R\{-1;1}
R\{1}
Tính tích phân
I = 3
Phần ảo của số phức
-2
1
2
-2i
Tính thể tích V của một khối trụ tam giác đều có đáy là tam giác đều cạnh 4a
Cho hình nón có diện tích xung quanh bằng và bán kính đáy bằng a. Độ dài đường sinh của hình nón đã cho bằng
3a
2a
Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Thể tích khối lăng trụ đã cho bằng
Cho khối lăng trụ đứng có , đáy ABC là tam giác vuông cân tại B và . Tính thể tích V của khối lăng trụ đã cho
Cho hình lăng trụ tam giác đều có . Thể tích khối lăng trụ bằng
Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh của hình nón là
Cho hình nón có chiều cao và bán kính đáy a. Tính diện tích xung quanh của hình nón
Trong không gian với hệ tọa độ Oxyz, cho . Mệnh đề nào sau đây đúng?
A(1;4;-5)
A(0;4;-5)
A(-1;-4;5)
A(0;-4;5)
Cho số phức z thỏa mãn . Tập hợp điểm biểu diễn số phức z là
một đường thẳng
một đường parabol
một đường elip
một đường tròn
Cho số phức z thỏa mãn . Tập hợp điểm biểu diễn số phức là
một đường tròn
một đường thẳng
Một elip
một parabol
Trong các mệnh đề sau, mệnh đề nào sai?
Nếu thì
thì A,B,C,D thẳng hàng
Với 3 điểm phân biệt A, B, C, nếu thì A, B, C thẳng hàng
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng và mặt phẳng . Tọa độ giao điểm A của d và (P) là
A(1;0;1)
A(0;0;-2)
(1;1;-6)
A(12;9;1)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt phẳng . Tọa độ giao điểm A của đường thẳng và mặt phẳng (P) là:
A(3;0;-1)
A(0;3;1)
A(0;3;-1)
A(-1;0;3)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng . Tọa độ điểm M à giao điểm của với mặt phẳng .
M(5;-1;-3)
M(1;0;1)
M(2;0;-1)
M(-1;1;1)
Tìm tất cả các giá trị thực của tham số m để hàm số liên tục trên R
m = 8
m = -8
Giá trị của tham số a để hàm số liên tục tại là
1
4
Giá trị của tham số m để hàm số liên tục tại là
m = 2
m = 1
m = 0
Cho hàm số lvới m là tham số thực. Tìm m để hàm số liên tục tại
m = 2
m = 1
m = -2
m = -1
Tính đạo hàm của hàm số
Tính đạo hàm của hàm số
Tính đạo hàm của hàm số
Tính đạo hàm của hàm số
1
0
2
3
Tích số tất cả các nghiệm thực của phương trình bằng
-1
1
Phương trình có tổng tất cả các nghiệm bằng
1
-1
Số nghiệm của phương trình bẳng
1
2
3
0
Số nghiệm của phương trình là:
2
1
3
0
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không là trung điểm của BC). Thiết diện của tứ diện bị cắt bởi mặt phẳng là
một tứ giác
một ngũ giác
một lục giác
một tam giác
Cho tứ diện ABCD. Gọi M là trung điểm của AB. Cắt tứ diện ABCD bởi mặt phẳng đi qua M và song song với BC và AD, thiết diện thu được là hình gì?
Tam giác đều
Tam giác vuông
Hình bình hành
Ngũ giác
Cho tứ diện ABCD. Trên các cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho . Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là
một tam giác
một hình bình hành
Một hình thang với đáy lớn gấp 2 lần đáy nhỏ
Một hình thang với đáy lớn gấp 3 lần đáy nhỏ
Cho tứ diện ABCD. Điểm M thuộc đoạn AC (M khác A, M khác C). Mặt phẳng đi qua M song song với AB và AD. Thiết diện của với tứ diên ABCD là hình gì?
hình tam giác
hình bình hành
hình vuông
hình chữ nhật
Cho hàm số có đồ thị (H), Số đường tiệm cận của (H) là
0
2
3
1
Đồ thị hàm số có tất cả bao nhiêu đường tiệm cận đứng?
3
1
0
2
Đồ thị hàm số có bao nhiêu đường tiệm cận?
4
3
2
1
Cho hàm số . Hãy chọn mệnh đề đúng trong các mệnh đề sau?
Đồ thị hàm số có hai tiệm cận ngang là và
Đồ thị hàm số có hai tiệm cận ngang là và , có tiệm cận đứng là
Đồ thị hàm số có tiệm cận ngang là , có tiệm cận đứng là
Đồ thị hàm số có tiệm cận ngang là , có tiệm cận đứng là
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
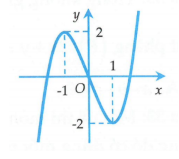
Cho hàm số có đồ thị như hình vẽ. Hỏi là đồ thị của hàm số nào?
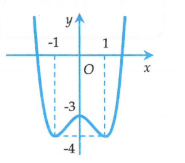
Đường cong trong hình bên là đồ thị của một hàm số nào dưới đây
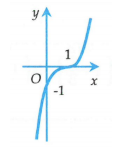
Đồ thị bên là đồ thị của hàm số nào sau?
Tập nghiệm của bất phương trình có dạng trong đó a, b là các số nguyên. Giá trị của biểu thức bằng
7
3
Cho F(x) là một nguyên hàm của hàm số . Biết , tính
Cho F(x) là một nguyên hàm của hàm số . Giá trị của bằng
Hàm số có một nguyên hàm F(x) thỏa mãn . Giá trị bằng:
Cho số phức . Tính
Cho số phức z thỏa mãn , tính
= 1
= 0
= 2
Cho số phức , tính
Cho hình chóp có 20 cạnh. Số mặt của hình chóp đó là
20
11
12
10
Một hình chóp có tất cả 2018 mặt. Hỏi hình chóp đó có bao nhiêu đỉnh?
1009
2018
2017
1008
Gọi n là số cạnh của hình chóp có 101 đỉnh. Tìm n
n = 202
200
n = 101
203
Tính diện tích miền hình phẳng giới hạn bới các đường ,
S = 2008
S = 2000
Diện tích của hình phẳng giới hạn bới đồ thị hàm số và trục hoành bằng
9
Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số:
S = 9
S = 27
Cho hình chóp S.ABC có tam giác ABC vuông tại B, SA vuông góc với mặt phẳng . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC
Cho hình chóp S.ABC có , tam giác ABC vuông tại B. Biết . Tính bán kính R của mặt cầu ngoại tiếp hình chóp
a
2a
Cho hình chóp S.ABCD có đáy là hình chữ nhật, . Đường thẳng SA vuông góc với đáy và . Thể tích của khối cầu ngoại tiếp hình chóp bằng
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với mặt đáy và . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD theo a
Trong không gian với hệ tọa độ Oxyz, xác định tọa độ điểm M' là hình chiếu vuông góc của điểm lên mặt phẳng
M'(3;4;2)
M'(1;3;5)
Trong không gian với hệ tọa độ Oxyz, cho điểm . Hình chiếu vuông góc của điểm A lên mặt phẳng là điểm M. Tọa độ điểm M là
M(1;-2;0)
M(0;-2;3)
M(1;0;3)
M(1;0;0)
Trong không gian với hệ tọa độ Oxyz, cho và mặt phẳng . Hình chiếu vuông góc của M lên mặt phẳng (P) là
H(2;5;3)
H(2;-3;-1)
H(6;7;8)
H(1;2;2)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3) và mặt phẳng . Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng
H(5;-6;7)
H(2;0;4)
H(3;-2;5)
H(-1;6;1)
Cho hàm số . Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên lần lượt là . Số giá trị của m để
2
0
1
4
Cho hàm số . Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên lần lượt là . Số giá trị của m để
2
0
1
4
Cho hàm số . Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên lần lượt là . Số giá trị của m để
2
0
1
4
Một gia đình cần ít nhất 900 đoen vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogram thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogram thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền của một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x, y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II. Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đòng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, BÌnh phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là
32 triệu đồng
35 triệu đồng
14 triệu đồng
30 triệu đồng
Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại vitamin A và B đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị vitamin cả A lẫn B và có thể tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B. Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A. Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng
600 đơn vị vitamin A, 400 đơn vị vitamin B
600 đơn vị vitamin A, 300 đơn vị vitamin B
500 đơn vị vitamin A, 500 đơn vị vitamin B
100 đơn vị vitamin A, 300 đơn vị vitamin B
Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc , đựng cao Sao vàng và đựng “Quy sâm đại bổ hoàn”. Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau
- Cách thứ nhất cắt được 3 hộp , một hộp cao Sao vàng và 6 hộp Quy sâm
- Cách thứ hai cắt được 2 hộp , 3 hộp cao Sao vàng và 1 hộp Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp tối thiểu là 900 hộp, số hộp cao Sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số tấm bìa phải dùng là ít nhất?
Cắt theo cách một tấm, cắt theo cách hai 300 tấm
Cắt theo cách một 150 tấm, cắt theo cách hai 100 tấm
Cắt theo cách một 50 tấm, cắt theo cách hai 300 tấm
Cắt theo cách một 100 tấm, cắt theo cách hai 200 tấm
Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm A và sản phẩm B trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy II trong 3 giờ, máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất
Sản xuất 9 tấn sản phẩm A và không sản xuất sản phẩm B
Sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm B
Sản xuất tấn sản phẩm A và tấn sản phẩm B
Sản xuất 6 tấn sản phẩm B và không sản xuất sản phẩm A
Trong không gian với hệ tọa độ Oxyz, cho điểm . Điểm nằm trên mặt phẳng sao cho mà . Biết , tính
Một đề thi môn Toán có 50 câu hỏi trắc nghiệm khách quan, mỗi câu hỏi có 4 phương án trả lời, trong đó có đúng một phương án là đáp án. Học sinh chọn đúng đáp án được 0,2 điểm, chọn sai đáp án không được điểm. Một học sinh làm đề thi đó, chọn ngẫu nhiên các phương án trả lời của tất cả 50 câu hỏi, xác suất để học sinh đó được 5,0 điểm bằng
Trong một bài thi trắc nghiệm khách quan có 10 câu. Mỗi câu có bốn phương án trả lời, trong đó chỉ có một phương án đúng. Mỗi câu trả lời đúng thì được 1 điểm, trả lời sai thì bị trừ 0,5 điểm. Một thí sinh do không học bài nên làm bài bằng cách với mỗi câu đều chọn ngẫu nhiên một phương án trả lời. Xác suất để thí sinh đó làm bài được số điểm không nhỏ hơn 7 là
Cho dãy số thỏa mãn , với mọi số nguyên . Tìm số tự nhiên n0 nhỏ nhất để
Cho dãy số thỏa mãn và với mọi . Giá trị nhỏ nhất của n để bằng
100
99
101
102
Cho dãy số xác định bởi: . Tổng bằng
Cho dãy số thỏa mãn và . Đặt . Tìm số tự nhiên n nhỏ nhất thỏa mãn
2587
2590
2593
2584
Cho dãy số thỏa mãn . Đặt . Tìm số nguyên dương lớn nhất n thỏa mãn
18
17
16
19
Cho hàm số với m là tham số. Có bao nhiêu giá trị nguyên để hàm số có nhiều điểm cực trị nhất?
2017
2018
4037
4035
Cho hàm số với m là tham số. Hỏi hàm số trên có thể có nhiều nhất bao nhiêu điểm cực trị?
1
2
3
4
Tổng các giá trị nguyên của tham số m để hàm số có 5 điểm cực trị là
2016
1952
-2016
-496
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số có 5 điểm cực trị
44
27
26
16
Cho hàm số . Tìm tất cả các giá trị của tham số m để hàm số có 5 điểm cực trị
Giá trị tham số thực k nào sau đây để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt
-1 < k < 1
k > 1
k < 1
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt?
4
3
1
2
Tìm tất cả các giá trị thực của tham số m để phương trình có ba nghiệm thực phân biệt
Cho đồ thị . Tất cả giá trị của tham số m để cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa mãn là
m = 1
m = 2
Cho biết sự tăng dân số được ước tinhd theo công thức . Đầu năm 2010 dân số tỉnh B là 1.038.229 người tính đến đầu năm 2015 dân số của tỉnh là 1.153.600 người. Hỏi nếu tỉ lệ tăng dân số àng năm giữ nguyên thì đầu năm 2020 dân số của tỉnh nằm trong khoảng nào?
(1.281.600;1.281.700)
(1.281.700;1.281.800)
(1.281.800;1.281.900)
(1.281.900;1.282.000)
Cho hàm số xác định trên thỏa mãn . Giá trị của biểu thức bằng
Cho hàm số xác định trên thỏa mãn .Tính
S = 1
S = 2ln2
Cho hàm số xác định trên và thỏa mãn
Tính giá trị của biểu thức
Cho bốn số phức khác không, phân biệt thỏa mãn các điều kiện: và . Tính
S = 2
Cho số phức z, biết rằng các điểm biểu diễn hình học của số phức z; iz và tạo thành một tam giác có diện tích bằng 18. Modun của số phức z bằng
6
9
Cho hình tứ chóp tứ giác có đáy là hình bình hành, trên các cạnh SA, SB, SC lần lượt lấy các điểm M, N, P sao cho . Mặt phẳng cắt cạnh SD tại Q. Biết thể tích khối chóp bằng. Tính thể tích V của khối chóp
V = 10
V = 12
V = 80
V = 8
Cho hình chóp tứ giác đáy là hình bình hành có thể tích bằng V. Lấy điểm B’, D’ lần lượt là trung điểm của cạnh SB và SD. Mặt phẳng qua cắt cạnh SC tại C’. Khi đó thể tích khối chóp bằng
Cho hàm số liên tục và có đạo hàm trên I thỏa mãn . Tính tích phân
I = -10
I = -5
I = 0
I = -18
Cho hàm số liên tục trên đoạn thỏa mãn và . Giá trị bằng
2
-1
-2
1
Cho hàm số liên tục trên đoạn và . Tính
I = 4
I = 2
I = 1
Cho liên tục trên đoạn và thỏa mãn Tích phân
30
28
36
16
Cho hàm số f(x) liên tục trên và . Tính tích phân
Cho hình thang ABCD vuông tại A và D, . Quay hình thang ABCD quanh đường thẳng CD. Thể tích khối tròn xoay thu được là:
Cho hình thang cân ABCD có đáy nhỏ ; đáy lớn , cạnh bên . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng
Cho lục giác đều ABCDEF có cạnh bằng 4. Quay lục giác đều đó quanh đường thẳng AD. Tính thể tích V của khối tròn xoay được sinh ra
Trong không gian với hệ tọa độ Oxyz, cho hình chóp với . Gọi I là tâm mặt cầu (S) ngoại tiếp hình chóp. Tính khoảng cách d từ I đến mặt phẳng (SAD)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có tâm ngoại tiếp hình chóp đều , , đỉnh . Khoảng cách từ S đến mặt phẳng bằng
3
1
Cho các só thực x, y, z thỏa mãn điều kiện . Hỏi biểu thức có thể nhận bao nhiêu giá trị nguyên?
2
1
3
4
Cho các số thực x, y, z thỏa mãn điều kiện . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức . Tính
Cho hai số thực x, y thỏa mãn . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức . Tính
Cho các số thực dương a, b, c thỏa mãn . Giá trị lớn nhất của nằm trong khoảng nào?
(1;4)
(4;8)
(8;10)
(10;14)
Cho số phức z thỏa mãn ; a, b, c dương. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức . Tính
Cho hàm số có đồ thị . Để đồ thị có 3 điểm cực trị cùng với nằm trên một parabol thì m nằm trong khoảng nào?
(-2;0)
(0;2)
(2;4)
Cho hàm số có đồ thị . Biết rằng trên tồn tại hai điểm phân biệt M, N mà tiếp tuyến tại đó có cùng hệ số góc m, đồng thời đường thẳng MN đi qua điểm . Hỏi m nằm trong khoảng nào?
(2017; 4000)
(-2019;0)
(0;2017)
Biết đồ thị hàm số (m là tham số) có ba điểm cực trị. Parabol đi qua ba điểm cực trị đó. Tính
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành tâm O; mặt phẳng vuông góc với mặt phẳng . Biết khoảng cách từ O đến mặt phẳng lần lượt là 1;2;. Tính khảng cách d từ O đến mặt phẳng
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và đường thẳng . Điểm nằm trên đường thẳng d sao cho từ M kẻ được ba tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) và . Tính
Cho hai hàm số có đồ thị như hình bên (hàm số có đồ thị là đậm hơn). Khi đó, tổng số nghiệm của hai phương trình và là
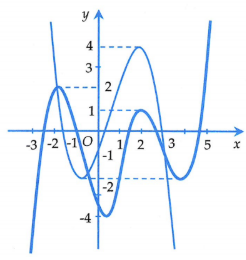
22
21
25
26
Gọi a là số thực lớn nhất để bất phương trình nghiệm đúng với mọi . Mệnh đề nào sau đây đúng?
Tính tổng S của tất cả các giá trị nguyên của m để bất phương trình nghiệm đúng với mọi x thuộc R
S = 12
S = 14
S = 35
S = 0
Số giá trị nguyên của tham số m để phương trình có ba nghiệm phân biệt là
0
1
2
3
Tập tất cả các giá trị của tham số thực m để phương trình có đúng hai nghiệm phân biệt là một nửa khoảng (a;b]. Tính

