49 câu hỏi
Trong không gian Oxyz, cho mặt cầu (S): . Tọa độ tâm T của (S) là
T(2;4;6).
T(1;2;3).
T(-2;-4;-6).
T(-1;-2;-3).
Điểm M(2;-2) là điểm cực tiểu của đồ thị hàm số nào?
Cho số phức z thỏa mãn (1+z)(1+i)-5+i=0. Số phức w=1+z bằng
-1+3i.
1-3i.
-2+3i.
2-3i
Dãy số nào sau đây không phải là một cấp số nhân?
1; 2; 3; 4; 5.
1; 2; 4; 8; 16.
1; -1; 1; -1; 1.
1; -2; 4; -8; 16.
Trong không gian Oxyz, cho mặt phẳng (P): x-2y+z-5=0. Trong các điểm A(0;0;5), B(1;1;3), C(-1;2;3), D(2;1;5), có bao nhiêu điểm thuộc mặt phẳng (P)?
4.
3.
2.
1.
Đồ thị hàm số nào dưới đây không có tiệm cận?
Nếu bằng
6
36
2.
4
Trong không gian Oxyz, phương trình mặt phẳng qua ba điểm A(-3;0;0),B(0;-2;0),C(0;0;1) được viết dưới dạng ax+by-6z+c = 0. Giá trị của T= a+b-c là
-7
-11.
11
-1
bằng
1
-1.
-
Cho hình hộp ABCD.A' B' C' D'. Mệnh đề nào sau đây sai?
(ABCD)//(A' B' C' D' ).
(AA' D' D)//(BCC' B' ).
(ACC' A' )//(BDD' B' ).
(ABB' A' )//(CDD' C' ).
Cho hai lực cùng tác động vào một vật tại điểm M cường độ hai lực lần lượt là 300N và 400N, . Tìm cường độ của lực tổng hợp tác động vào vật
0 N.
700N
100N
500N
Cho a là số thực thỏa mãn Giá trị của biểu thức bằng
0
2
1
3.
Cho m là một tham số thực và hai tập hợp A=[1-2m;m+3], . Tất cả các giá trị m để là:
Tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số có phương trình là
y= 9x- 7.
y= 6x- 4.
y= 2x.
y= -2x + 4.
Một hàm số bậc nhất y=f(x) có f(-1)=2 và f(2)= -3. Hàm số đó là:
y=-2x+3.
f(x)=
y=2x-3.
f(x)=
Tổng tất cả các hệ số của khai triển bằng 1024. Tìm hệ số của số hạng chứa trong khai triển biểu thức trên
120
210.
330
126
Cho lăng trụ tam giác đều ABC. có cạnh đáy bằng 2, độ dài đường chéo của các mặt bên bằng . Số đo góc giữa hai mặt phẳng và (ABC) là
Cho a,x,y dương; a khác 1. Đẳng thức nào sau đây đúng?
Một đội văn nghệ có 20 người, trong đó có 10 nam và 10 nữ. Hỏi có bao nhiêu cách chọn ra 5 người sao cho có ít nhất 2 nam và ít nhất 1 nữ trong 5 người đó.
12.900
13.125
550
15.504
Tập hợp điểm biểu diễn số phức z thỏa mãn là đường nào?
Một đường thẳng
Một đường parabol
Một đường tròn
Một đường elip
Tháp cột cờ quốc gia Lũng Cú thuộc huyện Đồng Văn tỉnh Hà Giang có đỉnh ở vị trí S, đáy thân tháp ở vị trí D. Hai vị trí A, B ở dưới thung lũng sao cho A, B, D, S cùng nằm trên một mặt phẳng và ở đó ta có thể quan sát được tháp đồng thời thực hiện đo đạc. H là hình chiếu vuông góc của S trên AB (hình vẽ).
Kết quả đo đạc như sau: AB = 15m, .
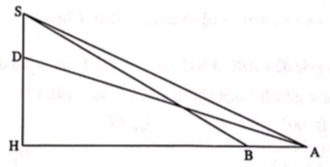
Chiều cao tháp cột cờ sấp sỉ bằng
20,6 m.
18,3 m.
26,2 m.
15,5 m.
Cho hàm số y = mcosx + sin2x (C) (m là tham số). Tìm tất cả các giá trị m để tiếp tuyến của (C) tại nhũng điểm có hoành độ song song hoặc trùng nhau.
Cho hai khối nón ( ),( ) . Chiều cao khối nón () bằng hai lần chiều cao khối nón () và đường sinh khối nón () bằng hai lần đường sinh khối nón (). Gọi lần lượt là thể tích hai khối nón (), (). Tỉ số bằng
Phương trình (sinx - cosx)(sinx + 2cosx - 3) = 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng ?
3
0.
1.
2.
Tập xác định của hàm số có dạng Tính a + b + c + d.
1.
-2.
3.
-4.
Cho hàm số y = f(x) có bảng biến thiên như sau.
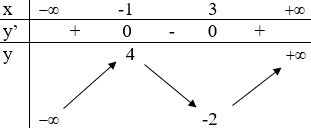
Số nghiệm của phương trình là
3.
5.
1.
2.
Cho hàm số y = f(x) xác định trên R và hàm số y = f'(x) có đồ thị như hình vẽ bên.
Khẳng định nào dưới đây là đúng?
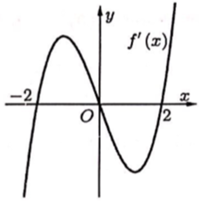
f(x) đạt cực đại tại x = 1.
f(x) đạt cực đại tại x = 0.
f(x) đạt cực đại tại x = -1.
f(x) đạt cực đại tại x = 2.
Trong không gian với hệ tọa độ Oxyz, cho A(1;2;3), B(3;4;4). Tìm tất cả các giá trị của tham số m sao cho khoảng cách từ điểm A đến mặt phẳng 2x + y + mz - 1 = 0 bằng độ dài đoạn thẳng AB.
m = 2.
m = -2.
m = -3.
m = 2
Cho hàm số y = f(x) có bảng biến thiên như sau.
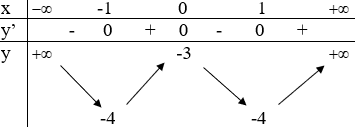
Mệnh đề nào dưới đây sai?
x = 1, x = -1 là các điểm cực tiểu và x = 0 là điểm cực đại của hàm số đã cho.
Hàm số nghịch biến trên các khoảng và (0;1).
Trên R hàm số có GTLN bằng -3 và GTNN bằng -4.
Hàm số đồng biến trên các khoảng (-1;0) và
Ông An gửi vào ngân hàng 60 triệu đồng theo hình thức lãi kép. Lãi suất ngân hàng là 8% trên năm. Sau 5 năm ông An tiếp tục gửi thêm 60 triệu đồng nữa. Hỏi sau 10 năm kể từ lần gửi đầu tiên ông An rút toàn bộ tiền cả gốc và lãi thì được số tiền gần nhất với số nào dưới đây? (Biết lãi suất không thay đổi qua các năm ông gửi tiền)
217.695.000 đồng.
231.815.000 đồng.
197.201.000 đồng.
190.271.000 đồng.
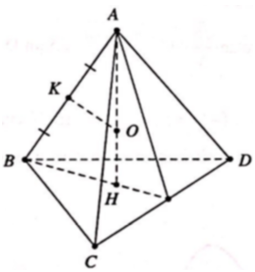
Cho hình chóp S.ABC có SA(ABC) tam giác ABC đều cạnh a và SA = a (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
1.
Cho hình phẳng (H) giới hạn bởi các đường y = , y = 0, x - 4. Đường thẳng y = k (0<k<16) chia hình (H) thành hai phần có diện tích S1, S2 (hình vẽ). Tìm k để S1 = S2.
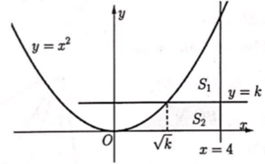
k = 8.
k = 4.
k = 5.
k = 3.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): và mặt phẳng (P): 2x - 2y + z + 3 = 0. Gọi M(a;b;c) là điểm trên mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Khi đó:
a + b + c = 8.
a + b + c = 5.
a + b + c = 6.
a + b + c = 7.
Biết rằng S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y = - 3(m-1)+ 3m(m+2)x nghịch biến trên đoạn [0;1]. Tính tổng các phần tử của S?
S = 0.
S = 1.
S = -2.
S = -1.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, mặt bên SAB là tam giác cân nằm trong mặt phẳng vuông góc với đáy, Tính thể tích mặt cầu (S) ngoại tiếp hình chóp.
Cho hàm số y = (với m là tham số khác 0) có đồ thị (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S = 1?
0.
1
2
3.
Trong giờ Thể dục, tổ 1 của lớp 12A1 có 12 học sinh gồm 5 nam và 7 nữa tập trung ngẫu nhiên thành một hàng dọc. Tính xác suất để người đứng đầu hàng và cuối hàng đều là nữ.
Cho hàm số f(x) xác định trên R thỏa mãn f' (x)=, f(0)=5 và .Giá trị của biểu thức bằng:
S= 31/2.
S= 9/2.
S= 5/2.
S= -7/2
Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua hai điểm A(1;-7;-8), B(2;-5;-9) sao cho khoảng cách từ điểm M(7;-1;-2) đến (P) lớn nhất có một véctơ pháp tuyến là =(a;b;4). Giá trị của tổng a+b là
-1.
3
6
2
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AD = 2cm, DC = 1cm, . Cạnh bên SB= cm, hai mặt phẳng (SAB) và (SBC) cùng vuông góc với mặt phẳng đáy. Gọi là góc tạo bởi SD và mặt phẳng (SAC). Tính
Trong mặt phẳng tọa độ Oxy, gọi (H1) là hình phẳng giới hạn bởi các đường và (H2) là hình gồm tất cả các điểm (x;y) thỏa mãn . Cho (H1) và (H2) quay quanh trục Oy ta được vật có thể tích lần lượt là V1, V2. Đẳng thức nào sau đây đúng
Gọi A là tập hợp tất cả các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc A. Tính xác suất để số tự nhiên được chọn chia hết cho 25
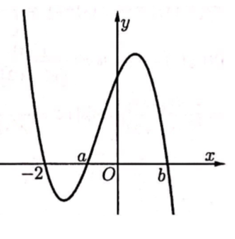
Cho hàm số y=f(x) có đồ thị y=f' (x) như hình vẽ. Để hàm số y= có 7 điểm cực trị thì mệnh đề nào dưới đây đúng?
f(a)>0>f(-2).
f(-2)>0>f(a).
f(b)>0>f(a).
f(b)>0>f(-2).
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn và f(1) = -3. Tính f(e).
-
-
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB = 2a. (ABCD) và SA=. Côsin của góc tạo bới hai mặt phẳng (SBC) và (SCD) bằng
Cho hàm số y=f(x) có đạo hàm trên R thỏa mãn f(-1)= f(3)= 0 và đồ thị hàm số y=f' (x) có dạng như hình vẽ. Hàm số y= nghịch biến trên khoảng nào trong các khoảng sau?
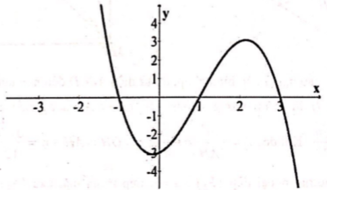
(-2;1).
(1;2).
(0;4).
(-2;2).
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB = 2a. (ABCD) và SA=. Côsin của góc tạo bới hai mặt phẳng (SBC) và (SCD) bằng
Cho tứ diện đều ABCD có mặt cẩu nội tiếp là (S1) và mặt cầu ngoại tiếp là (S2). Một hình lập phương ngoại tiếp (S2) và nội tiếp trong mặt cầu (S3). Gọi lần lượt là bán kính các mặt cầu (S1), (S2), (S3). Khẳng định nào sau đây là đúng
Cho hàm số y=f(x) có đạo hàm liên tục trên () thỏa mãn và f(1)=2. Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x = 2 là x
y = 16x+20.
y = -16x+20
y = -16x-20
y = 16x-20.

