Đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (Đề 19)
50 câu hỏi
Cho hàm số y = f(x) có bảng biến thiên như sau:
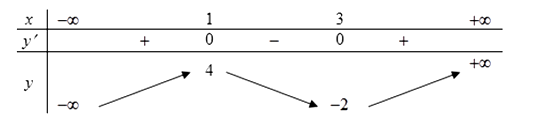
Hàm số y = f(x) đồng biến trên khoảng nào sau đây?
(1; 3)
Cho hàm số y = f(x) có đồ thị như hình vẽ.
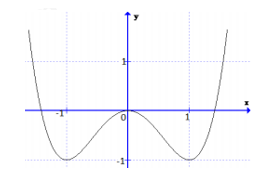
Mệnh đề nào dưới đây đúng?
Hàm số đạt cực đại tại x = -1và x = 1
Hàm số đạt cực tiểu tại x = 0
Hàm số đạt cực đại tại x = 0
Hàm số đạt cực đại tại x = 1
Đường cong ở hình bên dưới là đồ thị của hàm số với a, b, c, d là các số thực. Giá trị nhỏ nhất của hàm số trên đoạn [-1; 0] là
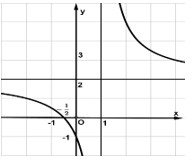
-1
1
0
2
Khẳng định nào đúng về tính đơn điệu của hàm số
Hàm số nghịch biến trên các khoảng và
Hàm số đồng biến trên các khoảng
Hàm số đồng biến trên các khoảng và
Hàm số nghịch biến trên các khoảng và
Cho hàm số Điểm cực đại của hàm số là:
x = 0
x = 2021
x = -1
x = 1
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là:
2
1
3
4
Số giao điểm của đồ thị hàm số và đồ thị hàm số là
3
1
2
0
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên [1; 2] bằng
0
-7
2
Gọi S tập hợp các giá trị m để đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác vuông cân. Tổng bình phương các phần tử của S bằng
2
4
8
6
Cho hàm số y = f(x) có bảng biến thiên như hình bên.
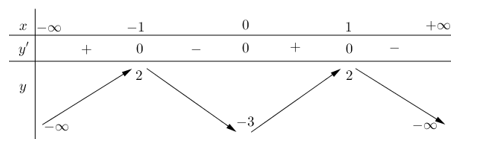
Hàm số y = f(1 - 2x) + 1 đồng biến trên khoảng
Cho hàm số y = f(x) có bảng biến thiên như hình bên.
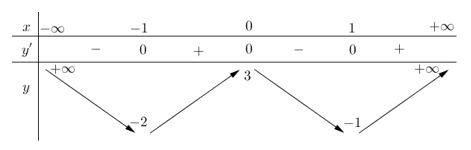
Phương trình có bao nhiêu nghiệm trên
3.
4
5
6
Cho hàm số y = f(x) có đạo hàm liên tục trên . Đồ thị y = f(x) như hình vẽ. Số đường tiệm cận đứng của đồ thị hàm số là
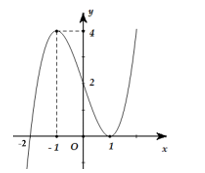
4
3
2
5
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ:
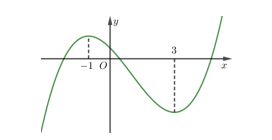
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số có 3 điểm cực trị. Tổng các phần tử của S là:
4
2
8
10
Cho ba số dương và số thực khác 0. Đẳng thức nào sai?
Đạo hàm của hàm số là
Tìm tập xác định D của hàm số
D = (-2; 1)
D = (1; 2)
D = [-2; 2]
Tổng tất cả các nghiệm của phương trình bằng
2
1
-2
-3
Tập nghiệm của bất phương trình: là
(0; 1]
(-2; 1]
Để lắp đặt hệ thống điện năng lượng mặt trời 50KWP, gia đình bạn A vay ngân hàngsố tiền là 600 triệu đồng với lãi suất 0,6%/tháng. Sau đúng một tháng kể từ ngày lắp đặt, gia đình bạn Abắt đầu đưa vào vận hành hòa lưới thì mỗi tháng công ty điện lực trả gia đình bạn A 16 triệu đồng. Nên sauđúng 1 tháng kể từ ngày vay, gia đình bạn A bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng,mỗi tháng hoàn nợ số tiền là 16 triệu đồng. Hỏi sau bao nhiêu tháng, gia đình bạn A sẽ trả hết nợ.
42
43
41
44
Cho phương trình Gọi S là tập hợp giá trị m nguyên với để phương trình có đúng 2 nghiệm. Tổng giá trị các phần tử của S bằng
-28
-12
-3
-27
Số giá trị m nguyên, , sao cho là
5
10
20
40
Cho hai hàm số f(x), g(x) liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
với mọi hằng số
với mọi hàm f(x)có đạo hàm trên
Cho hàm số f(x) liên tục và xác định trên [a; b]. Gọi F(x) là một nguyên hàm của hàm số f(x) Chọn phương án đúng nhất.
Nguyên hàm của hàm số f(x) = 2x(x - 1)(2x - 1)
Tìm nguyên hàm của hàm số biết f(1) = 0.
F(x) là một nguyên hàm của hàm Biết và Giá trị a + b bằng
17
9
12
18
Cho Giá trị a + 3b bằng
4
8
12
10
Cho hàm số y = f(x) có đạo hàm liên tục trên Giá trị bằng
Cho số phức z = a + bi (a, b ). Chọn phương án đúng.
Phần ảo của số phức zlà b
Phần ảo của số phức zlà bi
Phần thực của số phức zlà b
Mô đun của số phức zlà
Gọi là nghiệm của phương trình . Biết số phức có phần ảo âm. Phần ảo của số phức
i
-1
1
1 - i
Cho thỏa Phần ảo của số phức z là
0
4
-12
2
Cho thỏa Giá trị bằng
Có bao nhiêu khối đa diện đều
3
4
6
5
Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA = 2a. Thể tích của khối chóp.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Thể tích khối tứ diện ABDB' bằng
Cho hình chóp S.ABCD đáy ABCD là hình thoi cạnh a, góc Gọi I là trung điểm SC. Tính khoảng cách từ I đến mặt phẳng (SBD).
Cho hình lăng trụ ABCD.A'B'C'D' đáy là hình bình hành. Thể tích khối tứ diện BCDA' là
Khối trụ có bán kính đáy, đường cao lần lượt là a, 2a thì có thể tích bằng
Hình nón có bán kính đáy, đường cao lần lượt là 3, 4 thì diện tích xung quanh hìnhnón bằng
Từ một tấm tôn hình chữ nhật kích thước h và a người ta làm các thùng đựng nướchình trụ có chiều cao bằng h theo hai cách sau (xem hình minh họa dưới đây):
Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của mộtthùng.
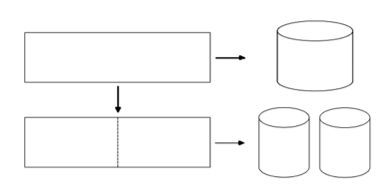
Kí hiệu là thể tích của thùng gò được theo cách 1 và là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số
Trong không gian Oxyz, gọi A là điểm thuộc mặt cầu tâm I bán kính R. Chọn phương án đúng.
IA < R
IA = R
IA > R
Trong không gian Oxyz điểm A(1; 2;3) thuộc phương trình mặt phẳng nào dưới đây.
Trong không gian Oxyz đường thẳng Ox có phương trình nào dưới đây
Trong không gian Oxyz, tọa độ hình chiếu của điểm M(1; 2; 3) lên mặt phẳng Oxz
(1; 0; 3)
(1; -2; 3)
(0; 2; 0)
(-1; 2; -3)
Trong không gian Oxyz phương trình mặt phẳng cắt tia Ox, Oy, Oz tại A, B, C và nhận làm trọng tâm của tam giác ABC
Trong không gian Oxyz tọa độ điểm đối xứng của điểm M(0; 1; 2) qua mặt phẳng x + y + z = 0
(-4; 2; 0)
(0; -1; -2)
(0; 1; -2)
(-2; -1; 0)
Trong không gian Oxyz, biết phương trình mặt cầu cắt mặt phẳng theo giao tuyến là một đường tròn có bán kính r. Khi đó giá trị của r là
4
5
3
Trong không gian Oxyz cho hai điểm Tìm tọa độ điểm sao cho MA = MB đạt giá trị nhỏ nhất
Cho hình lăng trụ . Số đoạn thẳng có hai đỉnh là đỉnh hình lăng trụ là
35
90
60
45
Có 6 học sinh gồm 2 học sinh trường A, 2 học sinh trường B và 2 học sinh trường C sắp xếp trên một hàng dọc. Xác suất để được cách sắp xếp mà hai học sinh trường C thì một em ngồi giữa hai học sinh trường A và một em ngồi giữa hai học sinh trường B là