50 câu hỏi
Cho F(x) là một nguyên hàm và Tìm hàm số
Hàm số có đạo hàm là:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình Phương trình mặt phẳng (P) tiếp xúc với mặt cầu tại điểm A(-1; -3; 4) là
Trong không gian Oxyz, mặt cầu có tâm I(4; -4; 2) và đi qua gốc tọa độ có phương trình là:
Cho hàm số y = f(x) có bảng biến thiên như sau:
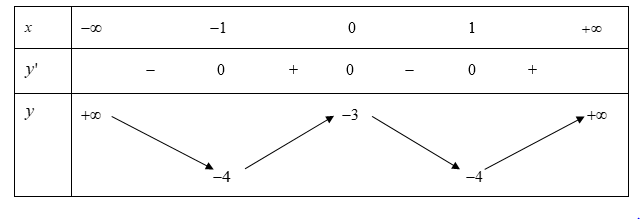
Giá trị cực đại của hàm số đã cho bằng
0
1
-3
-4
Trong không gian Oxyz, cho ba điểm Phương trình mặt phẳng đi qua ba điểm a, b, c có dạng Tính tổng S = a - b + c.
S = 10
S = 2
S = -2
S = -10
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình vẽ dưới
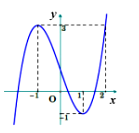
Số nghiệm thực của phương trình là:
2
0
1
3
Tập nghiệm S của phương trình là:
Nếu và thì bằng:
1
5
-5
-1
Cho hàm số y = f(x) liên tục trên [-1; 2] và có đồ thị như hình vẽ.
![Cho hàm số y = f(x) liên tục trên [-1; 2] và có đồ thị như hình vẽ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/blobid2-1652069834.png)
Biết diện tích các hình phẳng (K), (H) lần lượt là và Tính
Cho hàm số f(x) liên tục trên và có bảng xét dấu của f'(x) như sau:

Số điểm cực tiểu của hàm số đã cho là:
2.
1
0
3
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng và song song với nhau. Tính tổng S = m + n.
S = -8
S = -16
S = 8
S = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình Mặt phẳng nào dưới đây cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính bằng 3?
Tính thể tích khối tròn xoay tạo nên do quay xung quanh trục Ox hình phẳng (H) giới hạn bởi các đường và x = 2.
Số nghiệm nguyên của bất phương trình là:
5
Vô số
6
4
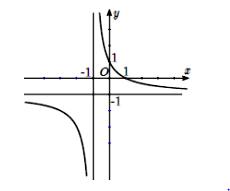
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới.
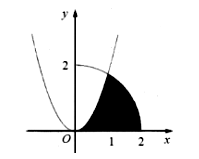
Cho (H) là hình phẳng giới hạn bởi parabol cung tròn có phương trình (với ) và trục hoành (phần tô dâm trong hình vẽ bên). Khối tròn xoay tạo ra khi (H) quay quanh Ox có thể tích V được xác định bằng công thức nào sau đây?
Cho tứ diện đều ABCD có cạnh đáy bằng a, M là trung điểm của CD. Tính cosin của góc giữa hai đường thẳng AC, BM.
0
Cho hình chóp S.ABCD có đáy là hình thang vuông tại vuông góc với mặt phẳng đáy. Góc giữa cạnh bên SC và mặt phẳng (ABCD) bằng Gọi I là trung điểm của cạnh AB. Tính khoảng cách từ điểm I đến mặt phẳng (SBC).
a
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là:
4
2
1
3
Có bao nhiêu cách chọn 3 học sinh từ một lớp gồm 35 học sinh?
Cho đồ thị của ba hàm số và (a, b, c là ba số dương khác 1 chotrước) được vẽ trong cùng một mặt phẳng tọa độ như hình bên. Chọn khẳng định đúng?
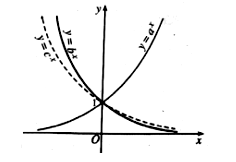
a > b > c
b > c > a
c > b > a
a > c > b
Giá trị nhỏ nhất của hàm số trên đoạn [1; 2] bằng:
1
33
12
0
Trong không gian Oxyz, cho mặt cầu (S) có phương trình Tọa độ tâm I và bán kính R của mặt cầu là:
Để dự báo dân số của một quốc gia, người ta sử dụng công thức trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2017 dân số Việt Nam là 93.671.600 người (Tổng cục thống kê, Niên giám thống kê 2017, Nhà xuất bản Thống kê, Tr.79). Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,81%, dự báo dân số Việt Nam năm 2030 là bao nhiêu người?
Cho hàm số y = f(x) có đồ thị như hình bên.
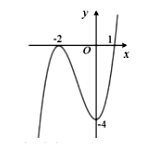
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
(-2; 0)
(-4; -2)
(-2; 1)
Cho cấp số nhân với và Công bội của cấp số nhân đã cho bằng:
4
3
8
12
Họ tất cả các nguyên hàm của hàm số trên khoảng là:
Trong không gian Oxyz, cho mặt phẳng Một vectơ pháp tuyến của mặt phẳng là:
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; -1; 3). Phương trình mặt phẳng qua các hình chiếu của M trên ba trục tọa độ là:
Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc S xác suất để số đó có hai chữ số tận cùng không có cùng tính chẵn lẻ bằng:
Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh 2a. Cạnh bên SA vuông góc với mặt phẳng đáy, SA = 2a. Tính thể tích V của khối chóp S.ABCD.
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử?
4.
3.
2.
1.
Cho tam giác đều ABC có cạnh bằng 4. Gọi H là trung điểm cạnh BC. Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AH là:
Cho đường thẳng y = 2x và parabol (c là tham số thực dương). Gọi và lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi thì c gần với số nào nhất sau đây?
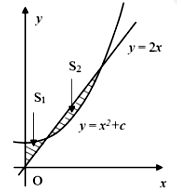
3
2
0
1
Diện tích hình phẳng (H) giới hạn bởi các đường là:
10 - 3ln2
10 - 2ln3
10 - ln3
Cho hình lăng trụ đứng ABC.A'B'C' có Gọi D là trung điểm của CC' và Tính thể tích V của khối lăng trụ ABC.A'B'C'.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của đỉnh S trên mặt phẳng đáy là điểm H sao cho Góc giữa cạnh SD và mặt phẳng (ABCD) bằng Tính thể tích V của khối chóp S.HCD.
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại cạnh bên SA tạo với mặt phẳng đáy góc Tính diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD.
Có bao nhiêu giá trị nguyên của m thuộc đoạn [-10; 10] để hàm số đồng biến trên khoảng
11
3
13
2
Cho hàm số f(x) liên tục trên [-1; 1] thỏa mãn Tích phân bằng:
Cho hàm số y = f(x) có bảng biến thiên:
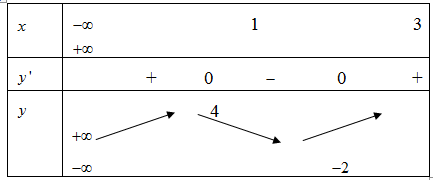
Có bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm phân biệt?
3
2
4
1
Cho là một nguyên hàm của hàm số Tìm họ nguyên hàm của hàm số
Một bạn sinh viên muốn có một khoản tiền để mua xe máy làm phương tiện đi làm sau khi ra trường. Bạn lên kế hoạch làm thêm và gửi tiết kiệm trong 2 năm cuối đại học. Vào mỗi đầu tháng bạn đều đặn gửi vào ngân hàng một khoản tiền T (đồng) theo hình thức lãi kép với lãi suất 0,56% mỗi tháng. Biết đến cuối tháng thứ 24 thì bạn đó có số tiền là 30 triệu đồng. Hỏi số tiền T gần với số tiền nào nhất trong các số sau?
1.139.450 đồng
1.219.000 đồng
1.116.000 đồng
1.164.850 đồng
Xét các số thực không âm x và y thỏa mãn Giá trị nhỏ nhất của biểu thức gần nhất với số nào dưới đây?
6
7
9
8
Cho vật thể có đáy là một hình tròn giới hạn bởi Biết rằng khi cắt vật thể bằng mặt phẳng vuông góc với trục Ox tại điểm có hoành độ thì được thiết diện là một hình vuông. Để thể tích V của vật thể đó bằng 2021 (đơn vị thể tích) thì R thuộc khoảng nào sau đây?
(6; 7)
(7; 8)
(9; 10)
(8; 9)
Cho hàm số f(x) liên tục và có đạo hàm trên [-2; 2] thỏa mãn Tính
Có tất cả bao nhiêu giá trị nguyên của sao cho đồ thị hàm số có đúng một tiện cận đứng?
2021
2015
2017
2016
Cho hàm số y = f(x)liên tục trên có bảng biến thiên như hình vẽ:
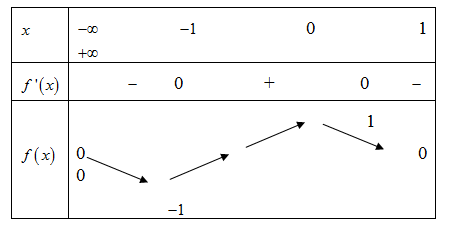
Số điểm cực đại của hàm số là:
2
0
1
3
Cho hai đường thẳng x'x, y'y chéo nhau và vuông góc với nhau. Trên x'x lấy cố định điểm A, trên y'y lấy cố định điểm B sao cho AB cùng vuông góc với Ax, By và AB = 2020 cm. Gọi CD là hai điểm lần lượt di chuyển trên hai tia Ax, By sao cho AC + BD = AD. Hỏi bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD có giá trị nhỏ nhất thuộc khoảng nào sau đây?
(1009; 1011)
(1427; 1429)
(2855; 2857)
(2019; 2021)
