66 CÂU HỎI
Phần tư duy đọc hiểu
Ý chính của bài viết là gì?
A. Nguyên nhân và hạn chế của chi phí logistics cao ở Việt Nam.
B. Hiệu quả của các phương thức vận chuyển và dịch vụ logistics.
C. Cách giảm chi phí logistics cho doanh nghiệp xuất nhập khẩu.
D. So sánh chi phí logistics của Việt Nam và các nước khác.
Đọc đoạn 1 và chỉ ra ngành logistics tại Việt Nam có những đóng góp nào sau đây?
Chọn hai đáp án đúng:
A. Đóng góp vào GDP 4-5%
B. Tăng trưởng ổn định nhất trong khu vực
C. Đứng thứ 4 tại khu vực Đông Nam Á về chỉ số logistics thị trường mới nổi
D. Đứng thứ 2 tại khu vực Đông Nam Á về doanh thu ngành logistics
Từ nội dung của đoạn 3, hãy hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Khu vực Cái Mép có 8 cảng container với tổng chiều dài các bến là 5.470m. Các bến cảng được phân tán ra nhiều nơi, tương đối cách xa nhau và đều có chiều dài cầu tàu khá ngắn (trung bình 600m bến/cảng)
A. Đúng
B. Sai
Từ nội dung của đoạn 2 và đoạn 4, hãy chỉ ra đâu là nguyên nhân khiến chi phí logistics của Việt Nam luôn ở mức cao?
Chọn 3 đáp án đúng:
A. Cơ sở hạ tầng hạn chế, thiếu đồng bộ
B. Chi phí vận tải hàng hoá bằng đường không quá cao so với đường bộ hay đường sắt
C. Chi phí vận tải hàng hoá bằng đường bộ quá cao so với đường thuỷ hay đường sắt
D. Phụ phí tại cảng biển mà chủ tàu container nước ngoài đang thu của chủ hàng Việt Nam
Từ nội dung của đoạn 7, hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Tiến sĩ KC Chang khuyên doanh nghiệp nên dùng dịch vụ hải quan của những nhà cung cấp có uy tín, chuyên nghiệp và có trình độ để giảm chi phí vận chuyển hàng hoá.
A. Đúng
B. Sai
Theo các chuyên gia tại Diễn đàn Logistics với khu vực châu Âu - châu Mỹ 2022, DN XNK nên thay đổi điều kiện bán hàng, mua hàng sang giá CIF thay vì FOB nhằm mục đích gì?
Chọn đáp án không đúng:
A. Chủ động hơn trong việc sử dụng các lịch vận chuyển phù hợp
B. Tăng cường khả năng cạnh tranh với các DN XNK khác
C. Tìm kiếm nguồn cung cấp cạnh tranh uy tín nhằm tiết kiệm chi phí cước tàu
D. Giảm thiểu các rủi ro trong quá trình vận chuyển
Đâu là lý do mà từ lâu nay người ta lại định giết mực?
Chọn đáp án đúng nhất:
A. Vì Mực rất ngon và béo
B. Vì Mực có nhiều nết xấu như tục ăn, nhiều vắt và sủa như gà gáy
C. Vì Mực hay cắn càn và làm phiền người ta
D. Vì Mực là con chó già và không còn ích lợi gì
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Người ta không thể nào tha thứ cho Mực vì Mực tham lam và bẩn thỉu.
Đúng hay sai?
A. Đúng
B. Sai
Đọc đoạn 5 và trả lời câu hỏi, tại sao Du thấy lòng nằng nặng?
Chọn đáp án đúng nhất:
A. Vì anh cảm thấy mất mát - con chó đã già đi và không còn như ngày xưa nữa
B. Vì anh không thể vuốt ve Mực như anh muốn khi thấy Mực ngày càng bẩn và yếu
C. Vì anh cảm thấy có lỗi với Mực khi đã bỏ rơi nó trong một thời gian dài
D. Vì anh không thể giúp Mực thoát khỏi cái chết cận kề
Từ nội dung của đoạn 6, hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Con chó vẫy đuôi mạnh hơn khi Du đưa chân chạm khẽ vào người nó. Nhưng nó lại len lén lánh ra vì nó sợ.
Đúng hay sai?
A. Đúng
B. Sai
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai từ nội dung đoạn 1.
Cái chết của con Mực là cái chết của tâm hồn người lao động.
Đúng hay sai?
A. Đúng
B. Sai
Xuyên suốt câu chuyện, đâu là những cảm xúc của Du khi gặp lại Mực? Chọn 3 đáp án Đúng
A. Thương hại
B. Bực mình
C. Nghẹn ngào
D.Vui mừng
Nếu Thí nghiệm 1 được lặp lại cho dụng cụ nấu ăn nhãn hiệu B với vật có khối lượng 200 gam, thì lực trung bình cần thiết để vật chuyển động sẽ gần nhất với:
A. 0,03N.
B. 0,06N.
C. 0,12N.
D. 0,18N.
Dựa vào kết quả của thí nghiệm 1 và 2, hãy cho biết sự kết hợp nào sau đây sẽ tạo ra bề mặt có hệ số ma sát nghỉ nhỏ nhất?
A. Dụng cụ nấu ăn nhãn hiệu A và nhãn hiệu bình xịt dầu X.
B. Dụng cụ nấu nướng nhãn hiệu B và nhãn hiệu bình xịt dầu Y.
C. Dụng cụ nấu ăn hiệu C và bình xịt dầu Y.
D. Dụng cụ nấu nướng nhãn hiệu C và bình xịt dầu Z.
Các nhận xét sau đây về thí nghiệm 2 là chính xác?
A. Nhãn hiệu dầu X sẽ tạo ra hệ số ma sát lớn nhất
B. Nhãn hiệu dầu Z được thực hiện thí nghiệm với 2 vật nặng khác nhau
C. Nhãn hiệu dầu Y tạo ra hệ số ma sát lớn nhất
Người hướng dẫn sinh viên đưa cho họ một dụng cụ nấu chống dính và yêu cầu họ xác định thương hiệu. Các học sinh lặp lại quy trình trong Thí nghiệm 1 và thu được lực trung bình là 0,088 N đối với vật 150 gam và 0,149 N đối với vật 250 gam. Thương hiệu nào sau đây rất có thể đã tạo ra những kết quả này?
A. Nhãn hiệu B.
B. Nhãn hiệu C
C. Chỉ có nhãn hiệu A và C.
D. Chỉ có nhãn hiệu B và C.
Theo đoạn văn, để học sinh đo chính xác hệ số ma sát tĩnh thì lực cần xác định đó là:
A. Trọng lượng của vật.
B. Lực giữa cân lò xo và vật.
C. Lực tác dụng của bình xịt nấu ăn lên bề mặt.
D. Lực cần thiết để làm vật di chuyển khỏi vị trí nghỉ
Trong thí nghiệm 1 học sinh dùng thêm chảo D, lực trung bình để kéo một vật nặng 200g trên chảo D là 0,02N. Khi đó ta có thể xác định được hệ số ma sát của chảo là bao nhiêu? Lấy g = 9,8m/s2
A. 0,01
B. 0,02
C. 0,03
D. 0,04
Dựa vào dữ liệu trong Thí nghiệm 1, biểu thức nào sau đây mô tả đúng nhất mối quan hệ giữa cường độ dòng điện, hiệu điện thế và điện trở? Cường độ dòng điện:
A. tăng khi tăng hiệu điện thế (V) và tăng khi tăng điện trở (Ω).
B. tăng khi tăng hiệu điện thế (V) và giảm khi tăng điện trở (Ω).
C. giảm khi tăng hiệu điện thế (V) và tăng khi tăng điện trở (Ω).
D. giảm khi tăng hiệu điện thế (V) và giảm khi tăng điện trở (Ω).
Trong một thí nghiệm bổ sung, các học sinh mắc một mạch điện tương tự như thí nghiệm 1, chỉ khác là sử dụng một pin 2V và một điện trở 5Ω, thì thấy cường độ dòng điện đo được trong mạch này là 0,400 A. Cường độ dòng điện phải là bao nhiêu, nếu học sinh mong đợi để họ tăng gấp đôi cả điện áp và điện trở?
A. 0,100 A
B. 0,400A
C. 0,800 A
D. 1.600 A
Bạc dẫn điện tốt hơn đồng một chút. Xem xét dữ liệu từ Thí nghiệm 3, giá trị nào sau đây có thể là điện trở của cuộn dây bạc dài 1 m?
A. 0,0202Ω
B. 0,0281Ω
C. 0,0414Ω
D. 0,0702Ω
Điện trở của chiều dài dây phụ thuộc vào độ dẫn điện của vật liệu: vật liệu có độ dẫn điện cao cung cấp điện trở thấp hơn vật liệu có độ dẫn điện thấp. Dựa vào dữ kiện ở thí nghiệm 2 và 3, hãy cho biết dãy nào sau đây sắp xếp các kim loại theo thứ tự độ dẫn điện tăng dần?
A. đồng, nhôm, vônfram, niken
B. vonfram, niken, nhôm, đồng
C. đồng, nhôm, niken, vonfram
D. niken, vonfram, nhôm, đồng
Các thí nghiệm 1-3 được hoàn thành trong phòng học ở nhiệt độ 20°C. Trong năm học trước, điều hòa không khí bị hỏng nên phòng thí nghiệm tương tự đã được hoàn thành ở nhiệt độ 28°C. Được biết, độ dẫn điện của kim loại giảm khi nhiệt độ tăng. Nhiệt độ lớp học cao hơn sẽ ảnh hưởng như thế nào đến điện áp cần thiết để đạt được 1 A trong Thí nghiệm 2?
A. Cần có cùng một lượng điện áp.
B. Cần nhiều điện áp hơn.
C. Cần ít điện áp hơn.
D. Không thể xác định từ thông tin được cung cấp.
Cho điện trở suất của đồng là ρ = 1,68.10−8 (Ω.m). Dây đồng trong thí nghiệm 3 sẽ có tiết diện là :
A. 7,58.10−7 (m2)
B. 8,75.10−7 (m2)
C. 7,85.10−7 (m2)
D. 8,85.10−7 (m2)
Hạt được tổng hợp từ thành phần nào có kích thước bé nhất?
A. Thành phần A.
B. Thành phần D.
C. Thành phần B.
D. Thành phần C.
Nhận định sau đây là đúng hay sai?
Nếu thời gian trộn tối thiểu để tạo ra các hạt siêu nhỏ là 5 giây thì có thể tạo ra các hạt siêu nhỏ có kích thước giống nhau.
A. Đúng
B. Sai
Có thể suy ra điều gì về ảnh hưởng của thời gian trộn đối với kích thước hạt nano?
A. Thời gian trộn kéo dài lên đến 20 giây không gây sự khác biệt về kích thước hạt nano, nhưng sau 20 giây, tăng độ trộn sẽ tăng kích thước hạt nano.
B. Tăng thời gian trộn sẽ tạo ra các hạt nano có kích thước lớn hơn.
C. Thời gian trộn kéo dài lên đến 20 giây tạo ra hạt nano có kích thước lớn hơn, nhưng sau 20 giây, không có sự khác biệt đáng kể về kích thước hạt.
D. Việc tăng thời gian trộn sẽ tạo ra các hạt nano có kích thước nhỏ hơn.
Chọn nhận định đúng trong những nhận định dưới đây:
Sau khi nhà khoa học thực hiện xong thí nghiệm, cô ấy đã lựa chọn được điều kiện tối ưu nhất để tổng hợp ra hạt có kích thước siêu nhỏ trong những thí nghiệm tiếp theo, với mục đích là tổng hợp được hạt có kích thước càng nhỏ càng tốt. Đó là:
A. Tổng hợp từ thành phần B.
B. Tổng hợp từ thành phần D.
C. Có PEG.
D. Không có PEG.
E. Thời gian khuấy là 15 giây.
F. Thời gian khuấy là 25 giây.
Thí nghiệm nào sau đây có thể giải quyết cuộc tranh luận giữa hai giáo sư?
A. Một thí nghiệm kiểm tra mức độ mạnh mẽ của liên kết hydro hiện diện trong các mẫu nước khác nhau ở các trạng thái khác nhau của vật chất và so sánh điều đó với động năng hiện tại.
B. Một thí nghiệm đo động năng trong các mẫu nước khác nhau.
C. Một thí nghiệm liên quan đến một hoặc nhiều khí trong đó kết quả thí nghiệm thực tế được tìm thấy được so sánh với kết quả được tìm thấy bởi cả hai phương trình.
D. Một thí nghiệm kiểm tra các loại khí khác nhau dựa trên các giá trị được tìm thấy trong Định luật khí lý tưởng.
Phát biểu sau đúng hay sai?
Giáo sư 2 sẽ đồng ý với phát biểu: “Luật khí lý tưởng phản ánh gần nhất các tương tác khí xảy ra trong tự nhiên”
A. Đúng
B. Sai
Cả hai giáo sư đều đồng ý với phát biểu nào sau đây?
A. Luật khí lý tưởng được sử dụng để mô phỏng dữ liệu thực nghiệm liên quan đến khí.
B. Phương trình Van der Waals được sử dụng để mô phỏng dữ liệu thực nghiệm liên quan đến khí.
C. Trạng thái của nước phụ thuộc vào năng lượng nhiệt của hệ thống.
D. Nước là bằng chứng của Lý thuyết Kinetic.
Cả hai giáo sư sẽ đồng ý với tuyên bố nào?
A. Lực lượng phân tán Luân Đôn là lực lượng duy nhất có mặt trong nước.
B. Nước là bằng chứng của Lý thuyết Kinetic.
C. Nước là một chất có mặt trên Trái đất ở dạng rắn, lỏng và khí.
D. Các cặp đơn độc có trên N, O và F có thể liên kết chặt chẽ hơn với các nguyên tử H trong nước.
Phát biểu nào của giáo sư 2 không mâu thuẫn với giáo sư 1?
A. Định luật Khí lý tưởng giải thích cho tất cả các lực xảy ra với chất khí.
B. Khi nhiệt độ tăng, động năng trung bình của các phân tử nước tăng.
C. Dữ liệu thực nghiệm phù hợp nhất liên quan đến nước ở trạng thái khí được tìm thấy bằng cách sử dụng Định luật Khí lý tưởng.
D. Không có lực hấp dẫn giữa các phân tử nước ở trạng thái khí.
Dựa trên kết quả 2 thí nghiệm, thức ăn nào cho kết quả tăng trọng nhiều nhất?
A. Thức ăn P .
B. Thức ăn S .
C. Thức ăn V .
D. Thức ăn Y.
Dựa vào kết quả của cả hai thí nghiệm, thành phần nào của thức ăn làm cho chuột lang phát triển tốt nhất?
A. Protein
B. Ngũ cốc
C. Trái cây và rau
D. Chất béo
Nhận định nào sau đây chính xác về mối quan hệ giữa trọng lượng và chiều dài của những con chuột lang được nghiên cứu?
A. Trọng lượng tỉ lệ nghịch với chiều dài cơ thể
B. Trọng lượng tỉ lệ thuận với chiều dài cơ thể
Một con chuột lang chọn ngẫu nhiên từ những con chuột được nghiên cứu, người ta đo các chỉ số của con chuột này có kết quả là 90g và 30cm. Con chuột này có thể thuộc nhóm?
A. Nhóm 1 .
B. Nhóm 6
C. Nhóm 2
D. Nhóm 7
Nhận định dưới đây đúng hay sai?
Theo kết quả thí nghiệm 3, thuốc R xâm nhập vào tế bào vi khuẩn nhanh nhất
A. Đúng
B. Sai
Nếu Thí nghiệm 2 được lặp lại với Thuốc U và thời gian ủ là 3 giờ, số lượng khuẩn lạc đếm được rất có thể là:
A. hơn 50.
B. giữa 41 và 50.
C. giữa 18 và 41.
D. nhỏ hơn 18
Phát biểu nào sau đây mô tả đúng nhất mối quan hệ giữa khối lượng phân tử và hệ số thấm của thuốc, trong Thí nghiệm 3?
A. Khi phân tử khối giảm thì hệ số thấm tăng.
B. Khi phân tử khối tăng thì hệ số thấm tăng.
C. Khi phân tử khối giảm dần thì hệ số thấm không đổi.
D. Khi khối lượng phân tử tăng thì hệ số thấm không đổi.
Phát biểu nào sau đây mô tả đúng nhất mối quan hệ giữa thời gian ủ và số lượng vi khuẩn sống trong Thí nghiệm 2?
A. Khi thời gian ủ tăng lên, số lượng vi khuẩn sống chỉ tăng lên.
B. Thời gian ủ tăng lên thì số lượng vi khuẩn sống chỉ giảm đi.
C. Thời gian ủ càng tăng thì số lượng vi khuẩn sống tăng nhanh, sau đó giảm dần.
D. Khi thời gian ủ tăng lên, số lượng vi khuẩn sống giảm nhanh, sau đó tăng chậm.
Trong thí nghiệm 1, mối quan hệ giữa nồng độ thuốc và hiệu quả của thuốc trong việc tiêu diệt vi khuẩn kháng penicillin là gì?
A. Không có mối quan hệ nào giữa nồng độ thuốc và hiệu quả của thuốc.
B. Một số loại thuốc hiệu quả nhất ở nồng độ thấp, một số loại khác hiệu quả nhất ở nồng độ cao.
C. Cả 5 loại thuốc đều đạt hiệu quả cao nhất ở nồng độ cao.
D. Cả 5 loại thuốc đều hiệu quả nhất ở nồng độ sử dụng thấp.
Hàm số nào sau đây nghịch biến trong khoảng (−∞;0)?
A. \[y = \sqrt 2 {x^2} + 1\].
B. \[y = - \sqrt 2 {x^2} + 1\].
C. \[y = \sqrt 2 {(x + 1)^2}\].
D. \[y = - \sqrt 2 {(x + 1)^2}\].
Xác định Parabol \((P):y = a{x^2} + bx + 2\) biết rằng Parabol đi qua hai điểm \(M(1;5)\) và \(N(2; - 2)\).
A. \(y = - 5{x^2} + 8x + 2\)
B. \(y = 10{x^2} + 13x + 2\)
C. \(y = - 10{x^2} - 13x + 2\)
D. \(y = 9{x^2} + 6x - 5\)
Tập hợp các giá trị của tham số \(m\) để hàm số \(y = {x^2} + (2m + 1)x - m + 3\) nghịch biến trên khoảng \(( - \infty ;2)\) là
A. \(\left[ { - \frac{5}{4}; + \infty } \right)\).
B. \(\left[ { - \frac{5}{2}; + \infty } \right)\).
C. \(\left[ {\frac{5}{4}; + \infty } \right)\).
D. \(\left( { - \infty ; - \frac{5}{2}} \right]\).
Phương trình \(m{x^2} - 2mx + 4 = 0\) vô nghiệm khi và chỉ khi
A. \(0 < m < 4\)
B. \(\left[ {\begin{array}{*{20}{l}}{m < 0}\\{m > 4}\end{array}} \right.\)
C. \(0 \le m \le 4\)
D. \(0 \le m < 4\)
Một công ty chuyên sản xuất đĩa CD với chi phí mỗi đĩa là 40 (nghìn đồng). Theo nghiên cứu nếu mỗi đĩa bán với giá x (nghìn đồng) thì số lượng đĩa bán được sẽ là q(x) = 120 − x, (x ∈ N*). Hãy xác định giá bán của mỗi đĩa sao cho lợi nhuận mà công ty thu được là cao nhất?
A. 60 nghìn đồng.
B. 70 nghìn đồng.
C. 80 nghìn đồng.
D. 90 nghìn đồng.
Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng toạ độ Oxy là một parabol có phương trình \(y = - \frac{1}{{10}}{x^2} + x\), trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất (tham khảo hình vẽ). Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O (khoảng cách này được gọi là tầm xa của quỹ đạo).
A. 6(m)
B. 7(m)
C. 13(m)
D. 10(m)
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ta lập được bao nhiêu số tự nhiên có 6 chữ số (các chữ số đôi một khác nhau), mà luôn có mặt nhiều hơn một chữ số lẻ và đồng thời trong đó hai chữ số kề nhau không cùng là số lẻ?
A. 38400
B. 38000
C. 35800
D. 34800
Trong không gian cho điểm A và mặt phẳng (P). Mệnh đề nào đưới đây đúng ?
A. Có đúng một mặt phẳng đi qua A và vuông góc với (P).
B. Có đúng hai mặt phẳng đi qua A và vuông góc với (P).
C. Có vô số mặt phẳng đi qua A và vuông góc với (P).
D. Không tồn tại mặt phẳng đi qua A và vuông góc với (P).
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt 2 \), biết các cạnh bên tạo với đáy một góc \({60^^\circ }\). Giá trị lượng giác tang của góc giữa hai mặt phẳng \((SAC)\) và \((SCD)\) bằng
A. \(\frac{{2\sqrt 3 }}{3}\).
B. \(\frac{{\sqrt {21} }}{3}\).
C. \(\frac{{\sqrt {21} }}{7}\).
D. \(\frac{{\sqrt 3 }}{2}\).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với \(AB = a,AD = a\sqrt 3 \). Hình chiếu vuông góc \(H\) của \(S\) trên mặt đáy trùng với trọng tâm tam giác ABC và \(SH = \frac{a}{2}\). Gọi M, N lần lượt là trung điểm các cạnh BC và SC. Gọi \(\alpha \) là góc giữa đường thẳng MN với mặt đáy \((ABCD)\). Mệnh đề nào sau đây đúng?
A. \(\tan \alpha = \frac{4}{3}\).
B. \(\tan \alpha = \frac{3}{4}\).
C. \(\tan \alpha = \frac{2}{3}\).
D. \(\tan \alpha = 1\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = {( - 1)^n}{.5^{2n + 3}}\). Mệnh đề nào sau đây đúng?
A. Dãy số \(\left( {{u_n}} \right)\) bị chặn trên và không bị chặn dưới.
B. Dãy số \(\left( {{u_n}} \right)\) bị chặn dưới và không bị chặn trên.
C. Dãy số \(\left( {{u_n}} \right)\) bị chặn.
D. Dãy số \(\left( {{u_n}} \right)\) không bị chặn.
Với hình vuông A1B1C1D1 như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tômàu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy định sau:
Bước 1: Tô màu "đẹp" cho hình vuông A1B1C1D1.
Bước 2: Tô màu "đẹp" cho hình vuông A2B2C2D2 là hình vuông ở chính giữa khi chia hình vuông A1B1C1D1 thành 9 phần bằng nhau như hình vẽ.
Bước 3: Tô màu "đẹp" cho hình vuông A3B3C3D3 là hình vuông ở chính giữa khi chia hình vuông A2B2C2D2 thành 9 phần bằng nhau. Cứ tiếp tục như vậy. Hỏi cần đúng bao nhiêu bước để tổng diện tích phần được tô màu chiếm \(\frac{{40}}{{81}}\)phần diện tích hình vuông ban đầu?
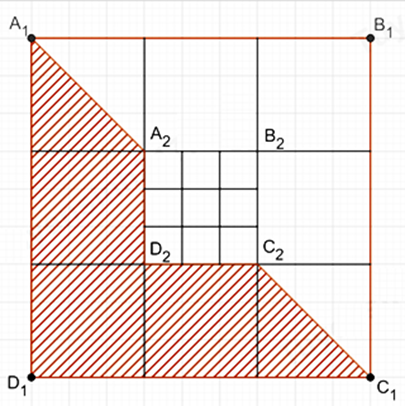
A. 2 bước
B. 4 bước
C. 5 bước
D. 6 bước
Giới hạn \(L = \lim \frac{{3n - 1}}{{n + 2}}\) bằng
A. +∞
B. 0
C. 1
D. 3
Từ khai triển biểu thức \({(x + 1)^{2023}}\) thành đa thức. Tổng các hệ số của đa thức là
A. \({2^{2023}}\)
B. 2023
C. \({2^{2022}}\)
D. 2024
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với \(M(0;10),N(100;10),P(100;0)\). Gọi \(S\) là tập hợp tất cả các điểm \(A(x;y)\,\,(x;y \in \mathbb{Z})\) nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm \(A \in S\). Xác suất để \(x + y \le 90\) là
A. \(\frac{{169}}{{200}}\).
B. \(\frac{{841}}{{1111}}\).
C. \(\frac{{86}}{{101}}\).
D. \(\frac{{473}}{{500}}\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA \bot (ABCD)\) và \(SA = a\sqrt 2 \). Khoảng cách giữa hai đường thẳng chéo nhau \({\rm{AC}}\) và \({\rm{SB}}\) bằng:
A. \(\frac{{a\sqrt {10} }}{5}\)
B. \(\frac{{3a}}{2}\)
C. \(\frac{{2a}}{3}\)
D. \(a\)
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A\) với \(AB = a,AC = 2a\). Mặt phẳng \((SBC)\) vuông góc với mặt phắng \((ABC)\). Mặt phẳng \((SAB),(SAC)\) cùng tạo với mặt phẳng \((ABC)\) một góc bằng \({60^^\circ }\). Gọi \(\alpha \) là góc giữa hai mặt phẳng \((SAB)\) và \((SBC)\). Tính \(\tan \alpha \).
A. \(\frac{{3\sqrt {17} }}{{17}}\).
B. \(\frac{{\sqrt {51} }}{{17}}\).
C. \(\frac{{\sqrt {17} }}{3}\).
D. \(\frac{{\sqrt {51} }}{3}\).
Hàm số nào sau đây là một hàm số tuần hoàn
A. \(y = x.\sin x\)
B. \(y = 2.\sin x + 3.\cos x\)
C. \(y = {x^2} + x + 1\)
D. \(y = \sin {x^2}\)
Một cầu thang đường lên cổng trời của một điểm giải trí ở công viên tỉnh X được hàn bằng sắt có hình dáng các bậc thang đều là hình chữ nhật với cùng chiều rộng là 35cm và chiều dài của nó theo thứ tự mỗi bậc đều giảm dần đi 7cm. Biết rằng bậc đầu tiên của cầu thang là hình chữ nhật có chiều dài 189cm và bậc cuối cùng cầu thang là hình chữ nhật có chiều dài 63cm. Hỏi giá thành làm cầu thang đó gần với số nào dưới đây nếu giá thành làm một mét vuông cầu thang đó là 1250 000 đồng trên một mét vuông?
A. 9500000 đồng.
B. 11000000 đồng.
C. 10000000 đồng.
D. 10500000 đồng
Có bao nhiêu giá trị thực của tham số m để phương trình \[(x - 1)(x - 3)(x - m) = 0\] có 3 nghiệm phân biệt lập thành cấp số nhân tăng?
A. 4
B. 3
C. 2
D. 1
Phương trình \(\frac{{4{{\cos }^2}x + 2\sin x - 5}}{{\tan x + \sqrt 3 }} = 0\) có bao nhiêu nghiệm?
A. 1 nghiệm
B. Vô số nghiệm
C. 2 nghiệm
D. Vô nghiệm
Tổng các nghiệm trên khoảng \((0;\pi )\) của phương trình lượng giác
\(4{\sin ^2}\frac{x}{2} - \sqrt 3 \cos 2x = 1 + 2{\cos ^2}\left( {x - \frac{{3\pi }}{4}} \right)\) là:
A. \(\frac{\pi }{{18}}\)
B. \(\frac{{20\pi }}{{18}}\)
C. \(\frac{{22\pi }}{{18}}\)
D. \(\frac{{37\pi }}{{18}}\)
Chọn mệnh đề đúng trong các mệnh đề sau:
A. Hàm số \(y = \cos x\) có đạo hàm tại mọi điểm thuộc miền xác định của nó.
B. Hàm số \(y = \tan x\) có đạo hàm tại mọi điểm thuộc miền xác định của nó.
C. Hàm số \(y = \cot x\) có đạo hàm tại mọi điểm thuộc miền xác định của nó.
D. Hàm số \(y = \frac{1}{{\sin x}}\) có đạo hàm tại mọi điểm thuộc miền xác định của nó.
Một vật chuyển động với quãng đường \(s(t) = - {t^3} + 12{t^2}\), với t là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s là quãng đường vật di chuyển được trong khoảng thời gian t. Hỏi trong khoảng thời gian 10 giây kể từ khi bắt đầu chuyển động, vật đạt được vận tốc lớn nhất bằng bao nhiêu?
A. 256 m/s.
B. 60 m/s.
C. 48 m/s.
D. 128 m/s.
