12 CÂU HỎI
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Căn bậc hai của 25 là
A. \(\sqrt 5 \) và \( - \sqrt 5 .\)
B. \( - 5\).
C. 5.
D. 5 và \( - 5\).
Rút gọn biểu thức\(\sqrt {64{a^2}} + 2a\) với \(a \ge 0\) ta được kết quả
A. \(16a.\)
B. \(10a\).
C. \(8a\).
D. \(6a\).
Điểm nào sau đây thuộc đồ thị hàm số \(y = 2{x^2}?\)
A. \(\left( {2;1} \right).\)
B. \(\left( {1;2} \right)\).
C. \(\left( {1;4} \right)\).
D. \(\left( {4;1} \right)\).
Các nghiệm của phương trình \(\left( {x + 2} \right)\left( {3x - 1} \right) = 0\) là
A. \(x = - 2\), \(x = - \frac{1}{3}.\)
B. \(x = - 2\), \(x = \frac{1}{3}.\)
C.\(x = 2\),\(x = - \frac{1}{3}.\)
D. \(x = 2\),\(x = \frac{1}{3}.\)
Lớp 9A có 40 học sinh, trong đó có 8 học sinh cận thị. Chọn ngẫu nhiên một học sinh của lớp, xác suất của biến cố “Học sinh được chọn không bị cận thị” là
A. \(\frac{1}{5}\).
B. \(\frac{8}{5}\).
C. \(\frac{4}{5}\).
D. \(\frac{2}{5}.\)
Nghiệm của bất phương trình \( - 2x - 4 > 0\) là
A. \(x > 2\).
B. \(x < 2\).
C. \(x < - 2\).
D. \(x > - 2\).
Đo chiều cao của học sinh lớp 9A ta có bảng tần số ghép nhóm sau:
|
Chiều cao (cm) |
\[\left[ {150;\,\,158} \right)\] |
\[\left[ {158;\,\,161} \right)\] |
\[\left[ {161;\,\,164} \right)\] |
\[\left[ {164;\,\,167} \right)\] |
|
Số học sinh |
5 |
12 |
15 |
8 |
Tần số tương đối của nhóm \[\left[ {158;\,\,161} \right)\] là
A. 12,5%.
B. 30%.
C. 37,5%.
D. 20%.
Số đo mỗi góc của một lục giác đều là
A.\(120^\circ \).
B.\(90^\circ \).
C. \(108^\circ \).
D. \(128^\circ \).
Cho hình nón có chiều cao 12 cm, bán kính đáy 5 cm. Độ dài đường sinh của hình nón đó là
A. 12 cm.
B. 13 cm.
C. 11 cm.
D. 10 cm.
Tính chiều cao của tháp canh trong hình bên (kết quả làm tròn đến hàngđơn vị).
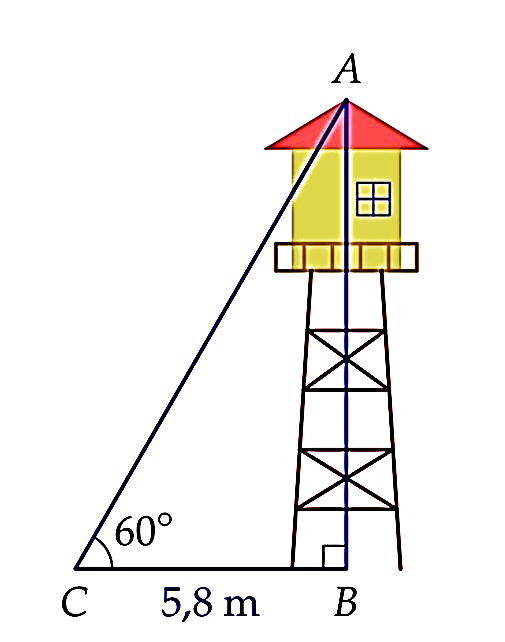
A. 12 m.
B. 13 m.
C. 11 m.
D. 10 m.
Một téc nước hình trụ có chiều cao 3 m, đường kính đáy 1 m. Thể tích nước tối đa mà téc nước chứa được là
A.\(\frac{1}{4}\pi \,\,({{\rm{m}}^3})\).
B.\(\frac{3}{4}\,\,({{\rm{m}}^3})\).
C. \(\frac{3}{4}\pi \,\,({{\rm{m}}^3})\).
D. \(\frac{4}{3}\pi \,\,({{\rm{m}}^3})\).
Cho tam giác \[ABC\] vuông tại \[A.\] Khẳng định nào sau đây là sai?
A. \(AB = BC.\cos B.\)
B. \(AC = AB.\sin B.\)
C. \(\tan B = \frac{{AC}}{{AB}}.\)
D. \(\cot B = \frac{{AB}}{{AC}}.\)
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải