20 CÂU HỎI
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Một mảnh đất hình vuông có diện tích bằng \(300\;{{\rm{m}}^2}\) thì độ dài cạnh của mảnh đất đó là bao nhiêu (kết quả tính theo đơn vị mét và làm tròn đến chữ số thập phân thứ nhất)?
A. \[17,4\;\;{\rm{m}}\].
B. \(17,3\;\;{\rm{m}}\).
C. \(17,0\;\;{\rm{m}}\).
D. \(17,32\;\;{\rm{m}}\).
Tất cả các giá trị của \(x\) để biểu thức \(\sqrt {2x - 4} \) xác định là
A. \(x \ge 0\).
B. \(x \ge 4\).
C. \(x \ge - 2\).
D. \(x \ge 2\).
Số đối của \(A = \sqrt[3]{{ - 8}} - \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} \) là
A. \(\sqrt 2 + 1\).
B. \(\sqrt 2 + 3\).
C. \(\sqrt 2 - 1\).
D. \(1 - \sqrt 2 \).
Cặp số \(\left( {x;y} \right)\) nào sau đây là nghiệm của phương trình \(3x - 2y = 7\)?
A. \(\left( { - 1; - 3} \right)\).
B. \(\left( {1; - 2} \right)\).
C. \(\left( {3; - 1} \right)\).
D. \(\left( {2; - 1} \right)\).
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{mx + 2y = n - 1}\\{x + \left( {n + 2} \right)y = 3}\end{array}} \right.\) có nghiệm \(\left( {x;y} \right) = \left( {2;1} \right)\). Khi đó giá trị của biểu thức \({m^2} + {n^2}\) bằng
A. 2.
B. 5.
C. 1.
D. 10.
Hai tổ công nhân cùng làm được 1200 sản phẩm. Biết rằng ba lần số sản phẩm của tổ II nhiều hơn hai lần số sản phẩm của tổ I là 350 sản phẩm. Hỏi tổ I làm được nhiều hơn tổ II bao nhiêu sản phẩm?
A. 20.
B. 30.
C. 50.
D. 100.
\(x = - 2\) là nghiệm của bất phương trình nào sau đây?
A. \(3x - \left( {x + 1} \right) > x - 1\).
B. \(3x + 4 > 2 - x\).
C. \(3 - x \ge 1 - 2x\).
D. \(2x < - 4\).
Phương trình \(\left( {m - 1} \right){x^2} + 3x + 2m = 0\) là phương trình bậc hai một ẩn \(x\) khi
A. \(m \ne 0\).
B. \(m \ne 1\).
C. \(m \ne - 1\).
D. \(m \in \mathbb{R}\).
Cho phương trình \({x^2} - x + m - 1 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1} + 2{x_2} = 5\). Khi đó giá trị của biểu thức \({x_2} - {x_1} - m\) bằng
A. \[ - 18.\]
B. \[ - 12.\]
C. 18.
D. 4.
Quan hệ giữa quãng đường chuyển động \(y\,\,({\rm{m}})\) và thời gian chuyển động \(x\) (giây) của một vật rơi tự do được biểu diễn gần đúng bởi công thức \(y = 5{x^2}\). Nếu thả một vật nặng từ độ cao 120 m xuống đất (coi sức cản của không khí không đáng kể) thì sau khi thả được bao nhiêu giây vật đó sẽ cách mặt đất 40 m?
A. 3 giây.
B. 6 giây.
C. 4 giây.
D. 2 giây.
Một người gieo một con xúc xắc cân đối đồng chất 40 lần liên tiếp, kết quả số lần xuất hiện mặt 1 chấm, 2 chấm, 3 chấm, 5 chấm, 6 chấm lần lượt là \(5;\,\,10;\,\,7;\,\,8;\,\,2\). Tính tần số tương đối xuất hiện của mặt 4 chấm.
A. \(20\% \).
B. \(\frac{1}{6}\).
C. \(25\% \).
D. \(10\% \).
Học sinh lớp 9A được giao làm một bài khảo sát trực tuyến môn Toán, kết quả \(100\% \) học sinh tham gia và thời gian làm bài kiểm tra của các học sinh được biểu diễn trong hình dưới đây:
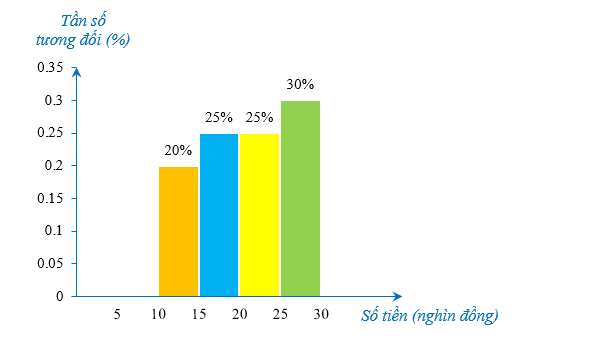
Biết có 8 học sinh làm xong bài kiểm tra trước 15 phút. Hỏi lớp 9A có bao nhiêu học sinh?
A. 45 học sinh.
B. 32 học sinh.
C. 40 học sinh.
D. 35 học sinh.
Cho tam giác đều \[MNP\]nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm
![Cho tam giác đều \[MNP\] nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/12-1741763486.png)
A. \[M,{\rm{ }}N,{\rm{ }}P.\]
B. \(M,\,\,P,\,\,N.\)
C. \[P,{\rm{ }}N,{\rm{ }}M.\]
D. \(N,\,\,P,\,\,M\).
Nhóm I có 4 học sinh nam và 2 học sinh nữ. Cô giáo chọn ngẫu nhiên 2 học \(\sinh \) của nhóm I để tham gia một trò chơi. Tính xác suất để 2 học sinh được chọn có ít nhất một học sinh nữ.
A. \(\frac{2}{3}\).
B. \(\frac{3}{5}\).
C. \(\frac{2}{5}\).
D. \(\frac{1}{3}\).
Biểu đồ ở hình bên cho biết tỉ lệ khối lượng các loại quả bán được trong ngày Chủ nhật của một cửa hàng. Biết khối lượng Nho xanh bán được là 24 kg. Khối lượng Vải thiều bán được là bao nhiêu?

A. 160 kg.
B. 40 kg.
C. 80 kg.
D. 60 kg.
Biết tứ giác \(MNPQ\)nội tiếp đường tròn \(\left( O \right)\) có \(\widehat {MNP} = 2\widehat {MQP}\). Số đo góc \(MOP\)bằng
A. \(90^\circ \).
B. \(60^\circ \).
C. \(240^\circ \).
D. \(120^\circ \).
Bán kính đường tròn ngoại tiếp hình vuông cạnh \(2\sqrt 2 \;{\rm{cm}}\) là
A. 4 cm.
B. 2 cm.
C. \(4\sqrt 2 \;{\rm{cm}}\).
D. \(\sqrt 2 \;{\rm{cm}}\).
Quả bóng rổ là một quả bóng hình cầu được sử dụng trong các trận đấu bóng rổ (hình vẽ), kích cỡ quả bóng rổ rất đa dạng dành cho các độ tuổi khác nhau. Quả bóng rổ size 7 có đường kính khoảng 24 cm, đây là kích cỡ bóng chính thức cho bóng rổ nam cấp độ trung học, đại học cũng như chuyên nghiệp. Khi bơm căng thì thể tích của quả bóng rổ size 7 là bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) (kết quả làm tròn đến chữ số hàng đơn vị)?

A. \[7\;238\;\;{\rm{c}}{{\rm{m}}^3}\].
B. \(7\;239\;\;{\rm{c}}{{\rm{m}}^3}\).
C. \(57\;905\;\;{\rm{c}}{{\rm{m}}^3}\).
D. \(57\;906\;\;{\rm{c}}{{\rm{m}}^3}\).
Bên trong một bể cá hình trụ bằng kính người ta đo được chiều cao là 50 cm và đường kính đáy là 20 cm (như hình vẽ). Người ta đổ nước vào bể đến khi mực nước trong bể cách mặt bể 10 cm thì dừng lại sau đó trang trí và thả cá vào bể. Tính thể tích nước đã đổ vào bể (kết quả tính theo đơn vị \({\rm{c}}{{\rm{m}}^3}\) và làm tròn đến chữ số thập phân thứ nhất).

A. \(3\;141,6\;\;{\rm{c}}{{\rm{m}}^3}\).
B. \(15\;708,0\;\;{\rm{c}}{{\rm{m}}^3}\).
C. \(12\;566,4\;\;{\rm{c}}{{\rm{m}}^3}\).
D. \(12\;566,3\;\;{\rm{c}}{{\rm{m}}^3}\).
Từ hai địa điểm \(A,\,\,B\) người ta cùng nhìn thấy một đỉnh núi với góc nâng lần lượt là \(40^\circ \) và \(30^\circ \) (như hình vẽ). Biết khoảng cách giữa hai địa điểm \(A,\,\,B\) là 600 m. Tính chiều cao của ngọn núi (kết quả tính theo đơn vị mét và làm tròn đến chữ số hàng đơn vị)?
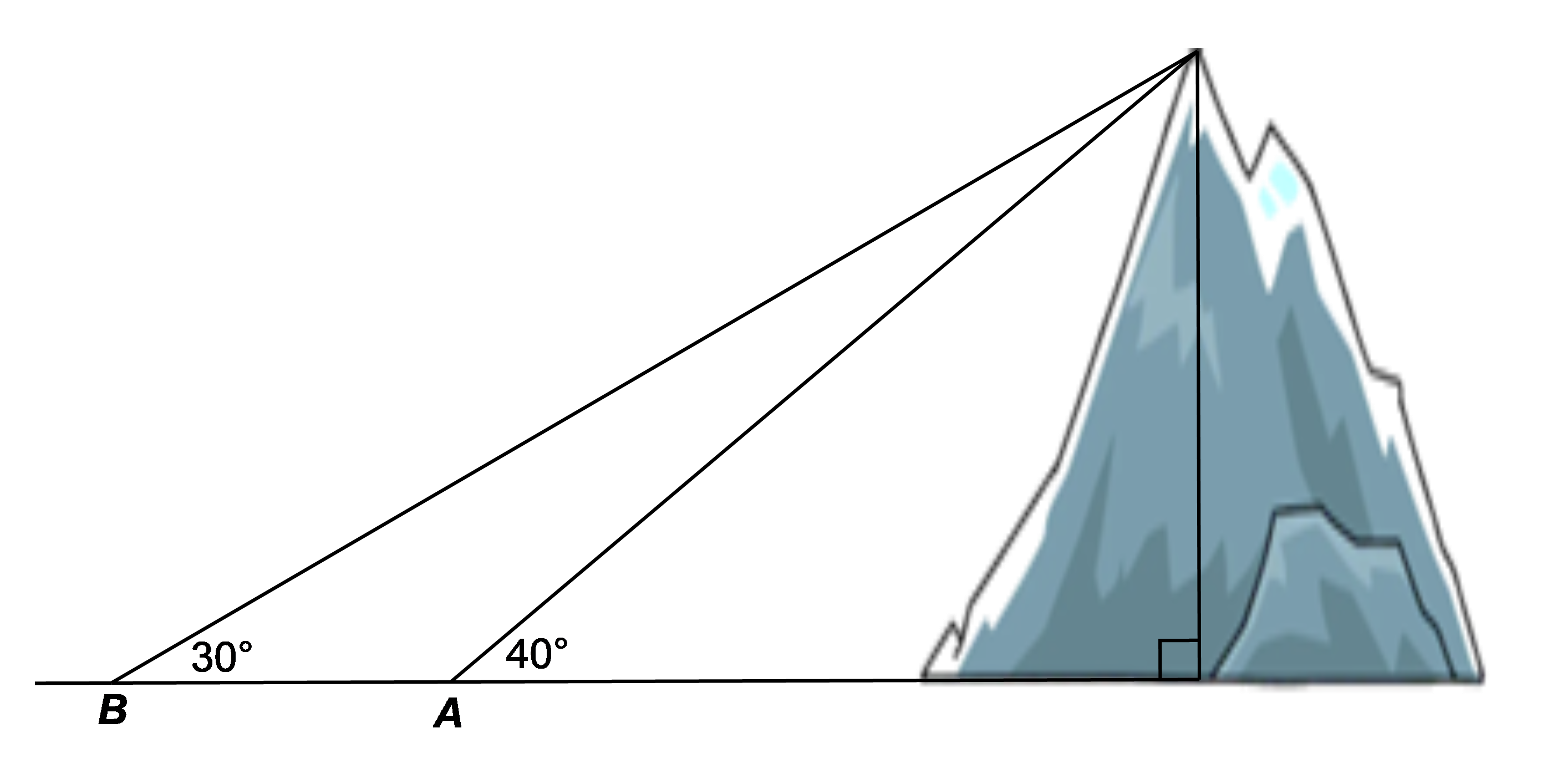
A. 1110 m.
B. 1111 m.
C. 1112 m.
D. 2292 m.

