12 CÂU HỎI
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
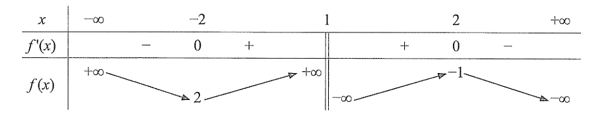
Số nghiệm của phương trình \(2f\left( x \right) - 3 = 0\) là
A. \(0\).
B. \(1\).
C. \(2\).
D. \(3\).
Hàm số nào dưới đây có đồ thị như hình vẽ.
A. \(y = \sin x\).
B. \(y = \cos x\).
C. \(y = \tan x\).
D. \(y = \cot x\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
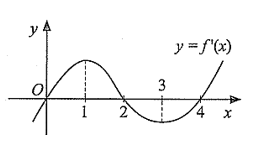
A. Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( { - \infty ;1} \right)\).
B. Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {2;4} \right)\).
C. Hàm số \(y = f\left( x \right)\) đạt cực tiểu tại \(x = 3\).
D. Hàm số \(y = f\left( x \right)\) đạt cực đại tại \(x = 4\).
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}},\left( {am \ne 0} \right)\) có đồ thị như hình vẽ bên. Phương trình đường tiệm cận xiên của đồ thị hàm số đã cho là:
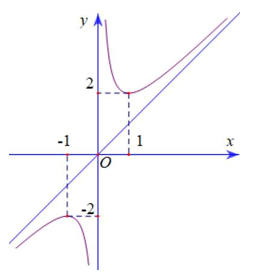
A. \(y = 2x\).
B. \(y = - x\).
C. \(y = x\).
D. \(y = - 2x\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3{x^2} + 2\;{\rm{khi}}\;x \le 1\\8x - 3\;{\rm{khi}}\;x > 1\end{array} \right.\). Khi đó giá trị của \(\int\limits_{ - 2}^2 {f\left( x \right){\rm{d}}x} \) bằng
A. \(0\).
B. \(24\).
C. \( - 12\).
D. \( - 6\).
Trong không gian toạ độ \[Oxyz\], vectơ nào sau đây là vectơ chỉ phương của đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = - 4 + 2t}\\{y = 7 - 3t}\\{z = 8 - 9t}\end{array}} \right.\)?
A. \[{\vec u_1} = \left( {4\,;7\,;\,8} \right)\].
B. \[{\vec u_1} = \left( { - 4\,;7\,;8} \right)\].
C. \[{\vec u_3} = \left( {2\,;3\,;9} \right)\].
D. \[{\vec u_4} = \left( {2\,; - 3\,; - 9} \right)\].
Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 10 hoặc bằng 10, biết rằng có ít nhất một con đã ra mặt 5 chấm.
A. \(\frac{6}{{11}}\).
B. \(\frac{4}{{11}}\).
C. \(\frac{5}{{11}}\).
D. \(\frac{3}{{11}}\).
Tập nghiệm \(S\) của bất phương trình \({5^{x + 2}} < {\left( {\frac{1}{{25}}} \right)^{ - x}}\) là
A. \(S = \left( { - \infty ;2} \right)\).
B. \(S = \left( { - \infty ;1} \right)\).
C. \(S = \left( {1; + \infty } \right)\).
D. \(S = \left( {2; + \infty } \right)\).
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, cạnh bên \(SA\) vuông góc với đáy. Biết khoảng cách từ \(A\) đến \(\left( {SBD} \right)\) bằng \(\frac{{6a}}{7}\). Tính khoảng cách từ \(C\) đến mặt phẳng \(\left( {SBD} \right)\).
A. \(\frac{{12a}}{7}\).
B. \(\frac{{3a}}{7}\).
C. \(\frac{{4a}}{7}\).
D. \(\frac{{6a}}{7}\).
Một mẫu số liệu ghép nhóm về chiều cao của một lớp (đơn vị là centimét) có phương sai là \(6,25\). Độ lệch chuẩn của mẫu số liệu đó bằng:
A. \(2,5\;{\rm{cm}}\).
B. \(12,5\;{\rm{cm}}\).
C. \(3,125\;{\rm{cm}}\).
D. \(42,25\;{\rm{cm}}\).
Trong không gian với hệ tọa độ \(Oxyz,\) khoảng cách từ điểm \(I\left( {1;1;1} \right)\) đến mặt phẳng \(\left( P \right):2x - y + z - 16 = 0\) bằng?
A. \( - 6\).
B. \(18\).
C. \(\frac{{7\sqrt 6 }}{3}\).
D. \( - 18\).
Trong không gian với hệ tọa độ\(Oxyz\), cho mặt cầu có phương trình \({x^2} + {y^2} + {z^2} - 2x + 4y - 6z - 11 = 0\). Tọa độ tâm \(I\) và bán kính \(R\) của mặt cầu đã cho lần lượt là
A. \(I\left( {1; - 2;3} \right),R = 5\).
B. \(I\left( {1;2; - 3} \right),R = 5\).
C. \(I\left( { - 1; - 2;3} \right),R = 5\).
D. \(I\left( {1; - 2; - 3} \right),R = 5\).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
