12 CÂU HỎI
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A. \(\left( {0;2} \right)\).
B. \(\left( {0; + \infty } \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( {1;2} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Điểm cực tiểu của hàm số đã cho là:
A. \( - 1\).
B. \(1\).
C. \(2\).
D. \( - 4\).
Giá trị lớn nhất của hàm số \(f\left( x \right) = 2 + 2x - {e^x}\) trên đoạn \(\left[ {0;2} \right]\) bằng
A. \(1\).
B. \(6 - {e^2}\).
C. \(\ln 2\).
D. \(2\ln 2\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Đường thẳng nào sau đây là đường tiệm cận ngang của đồ thị hàm số đã cho?
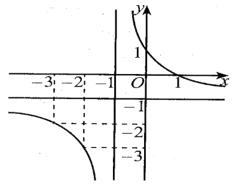
A. \(x = 1\).
B. \(x = - 1\).
C. \(y = 1\).
D. \(y = - 1\).
Cho hàm số \(y = f\left( x \right)\) là một nguyên hàm của hàm số \(y = {x^3}\). Phát biểu nào sau đây đúng?
A. \(f\left( x \right) = \frac{{{x^4}}}{4} + C\).
B. \(f\left( x \right) = 3{x^2}\).
C. \(f\left( x \right) = 4{x^3}\).
D. \(f\left( x \right) = \frac{{{x^4}}}{4}\).
Nếu hàm số \(f\left( x \right)\) thỏa mãn \(\int\limits_1^3 {f\left( x \right){\rm{d}}x} = 6\) và \(\int\limits_1^5 {f\left( x \right){\rm{d}}x = 20} \) thì giá trị của \(\int\limits_3^5 {f\left( x \right){\rm{d}}x} \) bằng
A. \( - 14\).
B. \(26\).
C. \(14\).
D. \(28\).
Một hộp chứa 4 viên bi xanh, 3 viên bi đỏ và 1 viên bi vàng. Các viên bi có cùng kích thước và khối lượng. Bạn Hà lấy ra ngẫu nhiên 1 viên bi từ hộp. Xác suất viên bi lấy ra không có màu vàng, biết rằng nó không có màu đỏ là
A. \(\frac{1}{2}\).
B. \(\frac{5}{8}\).
C. \(\frac{7}{8}\).
D. \(\frac{4}{5}\).
Xét mẫu số liệu ghép nhóm có tứ phân vị thứ nhất, tứ phân vị thứ hai, tứ phân vị thứ ba lần lượt là \({Q_1};{Q_2};{Q_3}\). Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó bằng
A. \({Q_2} - {Q_1}\).
B. \({Q_3} - {Q_2}\).
C. \({Q_3} - {Q_1}\).
D. \({Q_3} - 2{Q_2} + {Q_1}\).
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \(\left[ {0;2\pi } \right]\) là
A. \(3\).
B. \(1\).
C. \(2\).
D. \(4\).
Chỉ số hay độ \(pH\) của một dung dịch được tính theo công thức \(pH = - \log \left[ {{H^ + }} \right]\) với \(\left[ {{H^ + }} \right]\) là nồng độ ion hydrogen. Độ \(pH\) của một loại sữa có \(\left[ {{H^ + }} \right] = {10^{ - 6,8}}\) là bao nhiêu?
A. \( - 6,8\).
B. \(68\).
C. \(6,8\).
D. \(0,68\).
Trong không gian \(Oxyz\), cho điểm \(A\left( {1;2; - 1} \right)\) và mặt phẳng \(\left( P \right):x + 2y + z = 0\). Mặt phẳng \(\left( Q \right)\) qua \(A\) và song song với mặt phẳng \(\left( P \right)\) có phương trình là
A. \(x + 2y + z - 1 = 0\).
B. \(x + 2y + z + 4 = 0\).
C. \(x + 2y + z - 6 = 0\).
D. \(x + 2y + z - 4 = 0\).
Trong không gian \(Oxyz\), cho điểm \(I\left( {0; - 3;1} \right)\) và \(R = 2\). Mặt cầu tâm \(I\), bán kính \(R\) có phương trình là
A. \({x^2} + {\left( {y + 3} \right)^2} + {\left( {z - 1} \right)^2} = 4\).
B. \({x^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 4\).
C. \({x^2} + {\left( {y + 3} \right)^2} + {\left( {z - 1} \right)^2} = 2\).
D. \({x^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 2\).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
