35 CÂU HỎI
Trong các phát biểu sau, phát biểu nào không phải là mệnh đề?
A. 2 là số nguyên âm;
B. Bạn có thích học môn Toán không?
C. 13 là số nguyên tố;
D. Số 15 chia hết cho 2.
Trong các tập hợp sau, tập hợp nào là tập con của tập hợp A = {1; 2; 3; 4; 5}?
A. A1 = {1; 6};
B. A2 = {0; 1; 3};
C. A3 = {4; 5};
D. A3 = {0}.
Cho các tập hợp A = {x ∈ ℝ| – 5 ≤ x < 1} và B = {x ∈ ℝ| – 3 < x ≤ 3}. Tìm tập hợp A ∪ B.
A. A ∪ B = [– 5; 1);
B. A ∪ B = [– 5; 3];
C. A ∪ B = (– 3; 1);
D. A ∪ B = (– 3; 3].
Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình \[\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{2x - 3y + 2 > 0}\end{array}} \right.\].
A. (0; 0);
B. (1; 1);
C. (– 1; 1);
D. (– 1; – 1).
Mệnh đề nào sau đây đúng?
A. sin (180° – α) = – sin α;
B. cos (180° – α) = – cos α;
C. tan (180° – α) = tan α;
D. cot (180° – α) = cot α.
Tam giác ABC có BC = 1, AC = 3, \(\widehat C = 60^\circ \). Tính độ dài cạnh AB.
A. \(\sqrt {13} \);
B. \(\frac{{\sqrt {46} }}{2}\);
C. \(\frac{{\sqrt {34} }}{2}\);
D. \(\sqrt 7 \).
Cho lục giác đều ABCDEF tâm O như hình vẽ bên. Vectơ \(\overrightarrow {OB} \) cùng phương với vectơ nào sau đây?

A. \(\overrightarrow {OC} \);
B. \(\overrightarrow {BC} \);
C. \(\overrightarrow {BE} \);
D. \(\overrightarrow {OA} \).
Mệnh đề nào sau đây sai:
A. \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \);
B. \(\overrightarrow {MN} - \overrightarrow {MP} = \overrightarrow {PN} \);
C. \(\overrightarrow {MN} - \overrightarrow {NP} = \overrightarrow {MP} \);
D. \(\overrightarrow {MN} = \overrightarrow {IN} + \overrightarrow {MI} \).
Cho hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm. Tính \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right|\).
A. 5 cm;
B. 7 cm;
C. 9 cm;
D. 11 cm.
Cho G là trọng tâm của tam giác ABC và điểm M bất kỳ. Đẳng thức nào sau đây đúng?
A. \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {MG} \);
B. \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MG} \);
C. \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \);
D. \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 4\overrightarrow {MG} \).
Cho ba điểm A, B, C như hình vẽ:

Đẳng thức nào sau đây đúng?
A. \(\overrightarrow {MB} = 3\overrightarrow {MA} \);
B. \(\overrightarrow {MB} = \frac{1}{3}\overrightarrow {AB} \);
C. \(\overrightarrow {AB} = 4\overrightarrow {MA} \);
D. \(\overrightarrow {MB} = - 3\overrightarrow {MA} \).
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 2\overrightarrow i + \overrightarrow j \). Tìm tọa độ của vectơ \(\overrightarrow u \).
A. \(\overrightarrow u = \left( {2; - 1} \right)\);
B. \(\overrightarrow u = \left( { - 2;1} \right)\);
C. \(\overrightarrow u = \left( {2;1} \right)\);
D. \(\overrightarrow u = \left( { - 2; - 1} \right)\).
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây cùng phương?
A. \(\overrightarrow a = \left( {1;0} \right)\) và \(\overrightarrow b = \left( {0;1} \right)\);
B. \(\overrightarrow u = \left( {3; - 2} \right)\) và \(\overrightarrow v = \left( {6;4} \right)\);
C. \(\overrightarrow i = \left( {2;3} \right)\) và \(\overrightarrow j = \left( { - 6; - 9} \right)\);
D. \(\overrightarrow c = \left( {2;3} \right)\) và \(\overrightarrow d = \left( { - 6;9} \right)\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)khác vectơ-không. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow a ,\overrightarrow b } \right)\);
B. \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\);
C. \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\);
D. \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Miền nghiệm của bất phương trình 2x – y + 6 ≤ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
A.
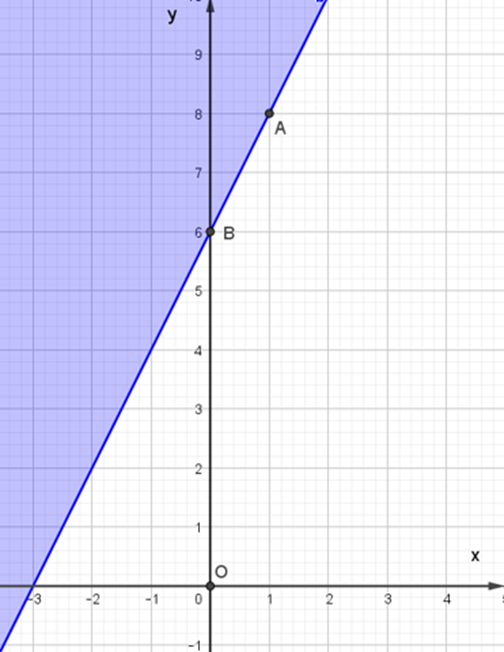
B.
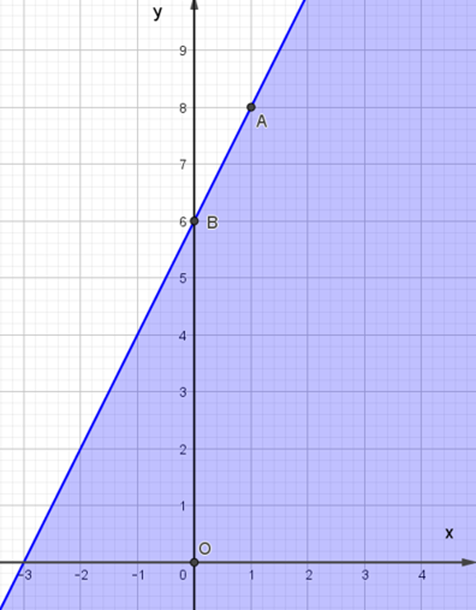
C.
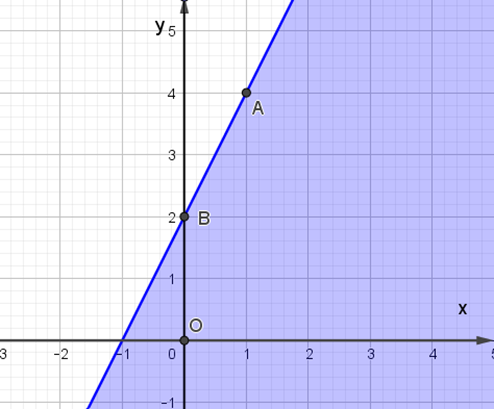
D.
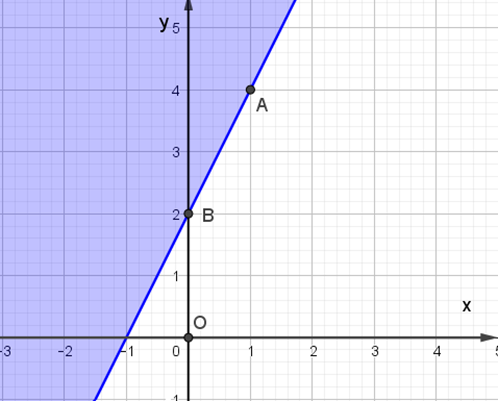
Cho tam giác ABC cân tại A có \[\widehat A = 120^\circ \]. Khi đó sin B bằng:
A. \(\frac{1}{2}\);
B. \( - \frac{1}{2}\);
C. \(\frac{{\sqrt 3 }}{2}\);
D.\( - \frac{{\sqrt 3 }}{2}\).
Cho góc α với 0° < α < 180°. Tính giá trị của cosα, biết \(\tan \alpha = - 2\sqrt 2 \).
A. \( - \frac{1}{3}\);
B. \(\frac{{2\sqrt 2 }}{3}\);
C. \(\frac{1}{3}\);
D. \(\frac{{\sqrt 2 }}{3}\).
Cho hình thoi ABCD. Vectơ – không có điểm đầu là A thì nó có điểm cuối là:
A. Điểm A;
B. Điểm B;
C. Điểm C;
D. Điểm D.
Cho tam giác ABC đều. Tính góc \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\).
A. 90°;
B. 135°;
C. 90°;
D. 60°.
Cho tam giác ABC có: AB = 3, BC = 4, AC = 5. Tính \(\overrightarrow {BA} .\overrightarrow {BC} \).
A. 1;
B. 0;
C. 12;
D. 20.
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Biết: \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 30^\circ \), \(\overrightarrow a .\overrightarrow b = \sqrt 3 \)và \(\left| {\overrightarrow b } \right| = 2\). Tính độ dài của vectơ \(\overrightarrow a \).
A. 1;
B. 2;
C. \(\frac{1}{2}\);
D. \(\frac{1}{4}\).
Một lực \(\overrightarrow F \) có độ lớn \(60\sqrt 3 \) N tác động vào điểm M làm vật di chuyển theo phương nằm ngang từ M đến điểm N cách M một khoảng 10 m. Biết góc giữa \(\overrightarrow F \) và phương thẳng đứng là 30°. Tính công sinh bởi lực F.
A. 900 J;
B. 800 J;
C. 600 J;
D. \(300\sqrt 3 \)J.
Cho giá trị gần đúng của \(\sqrt 3 \) là 1,73. Sai số tuyệt đối của số gần đúng 1,73 là:
A. 0,003;
B. 0,03;
C. 0,002;
D. 0,02.
Viết số quy tròn của số gần đúng b biết \(\overline b \) = 12 409,12 ± 0,5.
A. 12 410;
B. 12 409,1;
C. 12 000;
D. 12 409.
Tính số trung bình của mẫu số liệu sau:
2; 5; 8; 7; 10; 20; 11.
A. 8;
B. 9;
C. 10;
D. 11.
Tìm trung vị của mẫu số liệu sau:
0; 1; 2; 3; 5; 9; 10.
A. 3;
B. 5;
C. 0;
D. 2.
Số lượng học sinh đăng kí thi môn cầu lông các lớp từ lớp 6 đến lớp 9 được thống kê trong bảng dưới đây:
|
Lớp |
6 |
7 |
8 |
9 |
|
Số lượng |
20 |
25 |
22 |
15 |
Tìm mốt trong mẫu số liệu trên.
A. 6;
B. 7;
C. 8;
D. 9.
Cho mẫu số liệu sau:
5; 2; 9; 10; 15; 5; 20.
Tứ phân vị Q1, Q2, Q3 của mẫu số liệu trên lần lượt là:
A. 2; 5; 9;
B. 5; 9; 15;
C. 10; 5; 15;
D. 2; 9; 15.
Cho mẫu số liệu sau:
12; 5; 8; 11; 6; 20; 22.
Tính khoảng biến thiên của mẫu số liệu trên.
A.16;
B. 17;
C. 18;
D. 19.
Khoảng tứ phân vị ∆Q là
A. Q2 – Q1;
B. Q3 – Q1;
C. Q3 – Q2;
D. (Q1 + Q3) : 2.
Cho mẫu số liệu sau:
5; 6; 12; 2; 5; 17; 23; 15; 10.
Tính khoảng tứ phân vị của mẫu số liệu trên.
A. 8;
B. 9;
C. 10;
D. 11.
Cho mẫu số liệu sau:
10; 3; 6; 9; 15.
Tìm độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần trăm).
A. 3,03;
B. 4,03;
C. 5,03;
D. 6,03.
Cho tam giác đều ABC cạnh 4. Vectơ \( - \frac{1}{2}\overrightarrow {BC} \) có độ dài là.
A. 2;
B. 4;
C. 3;
D. 6.
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ \(\overrightarrow {AN} \) qua các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
A. \(\overrightarrow {AN} \) = \( - \overrightarrow {AC} + \frac{1}{2}\overrightarrow {AB} \);
B. \(\overrightarrow {AN} \) = \(\overrightarrow {AC} + \frac{1}{2}\overrightarrow {AB} \);
C. \(\overrightarrow {AN} \) = \( - \overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} \);
D. \(\overrightarrow {AN} \) = \(\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} \).
Trong mặt phẳng tọa độ Oxy cho ba điểm A(2; 1), B(1; 10) và điểm C(m; 2m – 17). Tất cả các giá trị của tham số m sao cho AB vuông góc với OC là
A. m = 9;
B. m = ±9;
C. m = – 9;
D. m = 1.

