12 CÂU HỎI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
![]() bằng
bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số![]() liên tục trên
liên tục trên ![]() và
và![]() thỏa mãn
thỏa mãn ![]() . Tìm mệnh đề đúng.
. Tìm mệnh đề đúng.
A.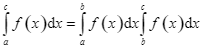 .
.
B.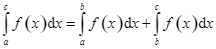 .
.
C. 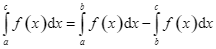 .
.
D. 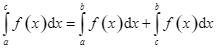 .
.
Cho hàm số ![]() liên tục trên
liên tục trên ![]() . Gọi
. Gọi ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() thỏa mãn
thỏa mãn ![]() . Khi đó
. Khi đó 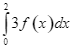 bằng
bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Diện tích của hình thang cong giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() được tính theo công thức
được tính theo công thức
A. ![]() .
.
B. ![]() .
.
C. 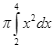 .
.
D. 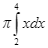 .
.
Tính 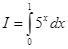
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Tính tích phân 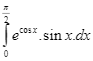 bằng
bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , mặt phẳng
, mặt phẳng ![]() có một vectơ pháp tuyến là
có một vectơ pháp tuyến là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho hai mặt phẳng
, cho hai mặt phẳng ![]() và
và ![]() (
(![]() là tham số). Tìm
là tham số). Tìm ![]() để
để ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ trục tọa độ ![]() , cho mặt phẳng
, cho mặt phẳng ![]() có phương trình
có phương trình ![]() và điểm
và điểm ![]() . Tính khoảng cách
. Tính khoảng cách ![]() từ
từ ![]() đến
đến ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho ba điểm
, cho ba điểm ![]() . Tọa độ nào sau đây là tọa độ vectơ pháp tuyến của mặt phẳng
. Tọa độ nào sau đây là tọa độ vectơ pháp tuyến của mặt phẳng ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() . Phương trình mặt phẳng trung trực của đoạn AB có một vectơ pháp tuyến là
. Phương trình mặt phẳng trung trực của đoạn AB có một vectơ pháp tuyến là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian hệ trục tọa độ ![]() , cho
, cho ![]() và mặt phẳng
và mặt phẳng ![]() . Viết phương trình mặt phẳng
. Viết phương trình mặt phẳng ![]() qua
qua ![]() và vuông góc với
và vuông góc với ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.

