12 CÂU HỎI
Cho hàm số \(f\left( x \right) = 3{x^2} + 2x\). Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\).
A. \({F_1}\left( x \right) = {x^3} + {x^2} - 4\).
B. \({F_2}\left( x \right) = \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2}\).
C. \({F_3}\left( x \right) = {x^3} - {x^2} + 1\).
D. \[{F_4}\left( x \right) = 3{x^3} + {x^2}\].
Mệnh đề nào dưới đây đúng?
A. \(\int\limits_1^2 {\frac{1}{{{e^x}}}} dx = \left. {\frac{1}{{{e^x}}}} \right|_1^2\).
B. \(\int\limits_1^2 {\frac{1}{{{e^x}}}} dx = \left. {{e^x}} \right|_1^2\).
C. \(\int\limits_1^2 {\frac{1}{{{e^x}}}} dx = \left. {{e^x}} \right|_2^1\).
D. \[\int\limits_1^2 {\frac{1}{{{e^x}}}} dx = \left. {\frac{1}{{{e^x}}}} \right|_2^1\].
Cho \(\int\limits_1^2 {f\left( x \right)dx} = \frac{1}{2},\int\limits_3^4 {f\left( x \right)dx} = \frac{3}{4}\). Kết quả \(\int\limits_1^4 {f\left( x \right)dx} - \int\limits_2^3 {f\left( x \right)dx} \) bằng
A. \(\frac{3}{8}\).
B. \(\frac{5}{4}\).
C. \(\frac{5}{8}\).
D. \(\frac{1}{4}\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \(D\) là diện tích hình phẳng giới hạn bởi đồ thị \(\left( C \right):y = f\left( x \right)\), trục hoành, hai đường thẳng \(x = - 2;x = 4\) (tham khảo hình vẽ bên dưới).
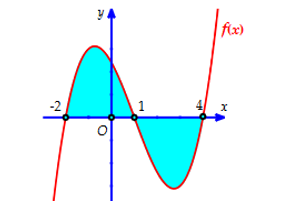
Giả sử \({S_D}\) là diện tích hình phẳng \(D\). Mệnh đề nào dưới đây sai?
A. \({S_D} = \int\limits_{ - 2}^4 {\left| {f\left( x \right)} \right|dx} \).
B. \({S_D} = \left| {\int\limits_{ - 2}^4 {f\left( x \right)dx} } \right|\).
C. \({S_D} = \left| {\int\limits_{ - 2}^1 {f\left( x \right)dx} } \right| + \left| {\int\limits_1^4 {f\left( x \right)dx} } \right|\).
D. \({S_D} = \int\limits_{ - 2}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
Tính \(I = \int\limits_0^2 {\frac{2}{{2x + 1}}dx} \).
A. \(I = \frac{1}{2}\ln 5\).
B. \(\ln 5\).
C. \(I = 4\ln 5\).
D. \(I = 2\ln 5\).
Cho vật thể \(\left( T \right)\) được giới hạn bởi hai mặt phẳng \(x = - 2;x = 2\). Biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\)(\( - 2 \le x \le 2\)) là một hình vuông có cạnh bằng \(\sqrt {4 - {x^2}} \). Thể tích vật thể \(\left( T \right)\) bằng.
A. \(\pi \).
B. \(\frac{{32}}{3}\).
C. \(\frac{{32\pi }}{3}\).
D. \(\frac{8}{3}\).
Trong không gian \(Oxyz\) cho mặt phẳng \(\left( P \right):x + 2y + 3z - 5 = 0\) có một vectơ pháp tuyến là
A. \(\overrightarrow {{n_3}} = \left( { - 1;2;3} \right)\).
B. \(\overrightarrow {{n_4}} = \left( {1;2; - 3} \right)\).
C. \(\overrightarrow {{n_2}} = \left( {1;2;3} \right)\).
D. \(\overrightarrow {{n_1}} = \left( {3;2;1} \right)\).
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1\) không đi qua điểm nào dưới đây:
A. \(P\left( {0;2;0} \right)\).
B. \(Q\left( {0;0;3} \right)\).
C. \(M\left( {1;2;3} \right)\).
D. \(N\left( {1;0;0} \right)\).
Trong không gian \(Oxyz\), phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {2; - 1;3} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {2;3; - 1} \right)\) là
A. \(\left( \alpha \right):2x + 3y - z - 2 = 0\).
B. \(\left( \alpha \right):2x + 3y - z + 2 = 0\).
C. \(\left( \alpha \right):2x - y + 3z - 2 = 0\).
D. \(\left( \alpha \right):2x - y + 3z + 2 = 0\).
Trong không gian \(Oxyz\), vectơ nào sau đây là một vectơ pháp tuyến của \(\left( P \right)\), biết \(\overrightarrow a = \left( { - 1; - 2; - 2} \right),\overrightarrow b = \left( { - 1;0; - 1} \right)\) là cặp vectơ chỉ phương của \(\left( P \right)\)?
A. \(\overrightarrow n = \left( {2;1;2} \right)\).
B. \(\overrightarrow n = \left( {2; - 1; - 2} \right)\).
C. \(\overrightarrow n = \left( {2;1; - 2} \right)\).
D. \(\overrightarrow n = \left( { - 2;1; - 2} \right)\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):2x - 2y + z - 1 = 0\). Khoảng cách từ điểm \(M\left( { - 1;2;0} \right)\) đến mặt phẳng \(\left( P \right)\) bằng
A. \(5\).
B. \(2\).
C. \(\frac{5}{3}\).
D. \(\frac{4}{3}\).
Trong không gian \(Oxyz\), cho điểm \(A\left( {2; - 1; - 3} \right)\) và mặt phẳng \(\left( P \right):3x - 2y + 4z - 5 = 0\). Mặt phẳng \(\left( Q \right)\) đi qua \(A\) và song song với mặt phẳng \(\left( P \right)\) có phương trình:
A. \(\left( Q \right):3x - 2y + 4z - 4 = 0\).
B. \(\left( Q \right):3x - 2y + 4z + 4 = 0\).
C. \(\left( Q \right):3x - 2y + 4z + 5 = 0\).
D. \(\left( \alpha \right):3x + 2y + 4z + 8 = 0\).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải