12 CÂU HỎI
Cho các hàm số \(f\left( x \right),g\left( x \right)\) có đạo hàm trên \(K\). Mệnh đề nào dưới đây sai?
A. \(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} + \int {g\left( x \right)dx} \).
B. \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} - \int {g\left( x \right)dx} \).
C. \(\int {g\left( x \right)dx} = g'\left( x \right) + C\).
D. \(\int {f'\left( x \right)dx} = f\left( x \right) + C\).
Nếu \(\int\limits_0^9 {f\left( x \right)dx} = 37\) và \(\int\limits_0^9 {g\left( x \right)dx} = 16\) thì \(\int\limits_0^9 {\left[ {2f\left( x \right) + 3g\left( x \right)} \right]dx} \) bằng
A. \(122\).
B. \(74\).
C. \(48\).
D. \(53\).
Nếu \(\int\limits_a^d {f\left( x \right)dx} = 5,\int\limits_b^d {f\left( x \right)dx} = 2\) với \(a < d < b\) thì \(\int\limits_a^b {f\left( x \right)dx} \) có giá trị bằng:
A. \( - 2\).
B. \(3\).
C. \(8\).
D. \(0\).
Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = {3^x},y = 0,x = 0\) và \(x = 2\). Mệnh đề nào dưới đây là đúng?
A. \(S = \pi \int\limits_0^2 {{3^x}dx} \).
B. \(S = \int\limits_0^2 {{3^{2x}}dx} \).
C. \(S = \int\limits_0^2 {{3^x}dx} \).
D. \(S = \pi \int\limits_0^2 {{3^{2x}}dx} \).
Tìm \(a\) để diện tích hình thang cong giới hạn bởi đồ thị \(\left( C \right):y = f\left( x \right) = \frac{2}{x},\) trục hoành và các đường thẳng \(x = 1,x = a\left( {a > 1} \right)\) bằng 2.
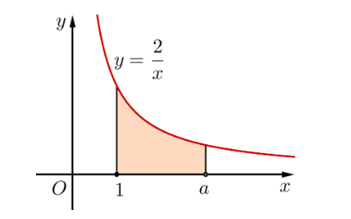
A. \({e^2}\).
B. \(e\).
C. \(2e\).
D. \(e + 1\).
Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}3{x^2}\;{\rm{khi}}\;0 \le x \le 1\\4 - x\;{\rm{khi}}\;1 < x \le 2\end{array} \right.\). Tính tích phân \(\int\limits_0^2 {f\left( x \right)dx} \).
A. \(\frac{7}{2}\).
B. \(1\).
C. \(\frac{5}{2}\).
D. \(\frac{3}{2}\).
Trong không gian \(Oxyz\), cho mặt phẳng \((P):3x - y + 2z - 1 = 0\). Vectơ nào dưới đây không phải là một vectơ pháp tuyến của \((P)\)?
A. \(\overrightarrow n = ( - 3;1; - 2)\).
B. \(\overrightarrow n = (3;1;2)\).
C. \(\overrightarrow n = (3; - 1;2)\).
D. \(\overrightarrow n = (6; - 2;4)\).
Trong không gian \[Oxyz\], cho mặt phẳng \[\left( P \right):x + y + z - 3 = 0\]. Chọn mệnh đề sai?
A. Điểm\[M\left( { - 1; - 1; - 1} \right)\] không thuộc mặt phẳng \(\left( P \right)\).
B. Điểm\[N\left( {1;1;1} \right)\] thuộc mặt phẳng \(\left( P \right)\).
C. Điểm\(K\left( { - 3;0;0} \right)\) không thuộc mặt phẳng \(\left( P \right)\).
D. Điểm\(Q\left( {0;0; - 3} \right)\) thuộc mặt phẳng \(\left( P \right)\).
Khoảng cách từ điểm \[M\left( {3;\,\,2;\,\,1} \right)\] đến mặt phẳng (P): \(Ax + Cz + D = 0\), \(A.C.D \ne 0\). Chọn khẳng định đúng trong các khẳng định sau:
A. \(d(M,(P)) = \frac{{\left| {3A + C + D} \right|}}{{\sqrt {{A^2} + {C^2}} }}\).
B. \[d(M,(P)) = \frac{{\left| {A + 2B + 3C + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\]
C. \(d(M,(P)) = \frac{{\left| {3A + C} \right|}}{{\sqrt {{A^2} + {C^2}} }}.\)
D. \[d(M,(P)) = \frac{{\left| {3A + C + D} \right|}}{{\sqrt {{3^2} + {1^2}} }}.\]
Trong không gian \(Oxyz\), phương trình của mặt phẳng đi qua điểm \(A\left( {3;0; - 1} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {4; - 2; - 3} \right)\) là
A. \(4x - 2y + 3z - 9 = 0\).
B. \(4x - 2y - 3z - 15 = 0\).
C. \(3x - z - 15 = 0\).
D. \(4x - 2y - 3z + 15 = 0\).
Trong không gian \(Oxyz\), khoảng cách giữa hai mặt phẳng \(\left( P \right):x + 2y + 2z - 10 = 0\) và \(\left( Q \right):x + 2y + 2z - 3 = 0\)bằng:
A.\(\frac{4}{3}\)
B.\(\frac{8}{3}\).
C.\(\frac{7}{3}\).
D.\(3\).
Trong không gian với hệ tọa độ \(Oxyz\), cặp vectơ \(\overrightarrow a = \left( {2;1; - 2} \right),\overrightarrow b = \left( {1;0;2} \right)\) có giá song song với mặt phẳng \(\left( P \right)\). Phương trình mặt phẳng \(\left( P \right)\)qua \(C\left( {1;1;3} \right)\) là
A. \(2x + 6y - z - 7 = 0\).
B. \(2x - 6y - z + 5 = 0\).
C. \(2x + 6y + z + 5 = 0\).
D. \(2x - 6y - z + 7 = 0\).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải