11 CÂU HỎI
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = 2x + 5\) là
A. \({x^2} + 5x + C.\)
B. \(2{x^2} + 5x + C.\)
C. \(2{x^2} + C.\)
D. \({x^2} + C.\)
Mệnh đề nào dưới đây đúng?
A. \({\left( {\int {f\left( x \right){\rm{d}}x} } \right)^\prime } = f'\left( x \right)\).
B. \({\left( {\int {f\left( x \right){\rm{d}}x} } \right)^\prime } = - f\left( x \right)\).
C. \({\left( {\int {f\left( x \right){\rm{d}}x} } \right)^\prime } = - f'\left( x \right)\).
D. \({\left( {\int {f\left( x \right){\rm{d}}x} } \right)^\prime } = f\left( x \right)\).
Biết \[\int\limits_0^1 {f\left( x \right)dx = - 2} \] và \[\int\limits_0^1 {g\left( x \right)dx = 3} ,\] khi đó \[\int\limits_0^1 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \] bằng
A. \[ - 5.\]
B. \[5.\]
C. \[ - 1.\]
D. \[1.\]
Cho \(f\left( x \right)\) là hàm số liên tục trên đoạn \(\left[ {1;2} \right]\). Biết \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) thỏa mãn \(F\left( 1 \right) = - 2\) và \(F\left( 2 \right) = 4\). Khi đó \(\int\limits_1^2 {f\left( x \right){\rm{d}}} x\) bằng
A. \(6\).
B. \(2\).
C. \( - 6\).
D. \( - 2\).
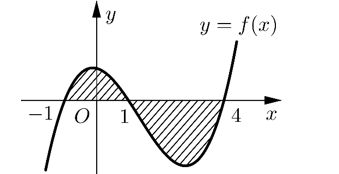
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 1\) và \(x = 4\) (như hình vẽ bên). Mệnh đề nào dưới đây là đúng?
A. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
B. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
C. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
D. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \frac{{2x - 1}}{{{{\left( {x + 1} \right)}^2}}}\) trên khoảng \(\left( { - 1; + \infty } \right)\) là
A. \(2\ln \left( {x + 1} \right) + \frac{2}{{x + 1}} + C\).
B. \(2\ln \left( {x + 1} \right) + \frac{3}{{x + 1}} + C\).
C. \(2\ln \left( {x + 1} \right) - \frac{2}{{x + 1}} + C\).
D. \(2\ln \left( {x + 1} \right) - \frac{3}{{x + 1}} + C\).
Trong không gian \(Oxyz\), phương trình của mặt phẳng \[\left( {Oxy} \right)\] là
A. \(y = 0\).
B. \(x = 0\).
C. \(z = 0\).
D. \(x + y = 0\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right):3x + 2y - 4z + 1 = 0\). Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( \alpha \right)\)?
A. \(\overrightarrow {{n_2}} = \left( {3\,;\,2\,;\,4} \right)\).
B. \(\overrightarrow {{n_3}} = \left( {2\,;\, - 4\,;\,1} \right)\).
C. \(\overrightarrow {{n_1}} = \left( {3\,;\, - 4\,;\,1} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {3\,;\,2\,;\, - 4} \right)\).
Trong không gian \(Oxyz\), mặt phẳng đi qua \(O\) và nhận vectơ \(\overrightarrow n = \left( {1;\, - 2;\,5} \right)\) làm vectơ pháp tuyến có phương trình là
A. \(x + 2y - 5z = 0\).
B. \(x + 2y - 5z + 1 = 0\).
C. \(x - 2y + 5z = 0\).
D. \(x - 2y + 5z + 1 = 0\).
Mặt phẳng \[(P)\] song song với giá của hai vectơ \(\overrightarrow {{u_1}} = \left( { - 1; - 3; - 3} \right),\;\,\overrightarrow {{u_2}} = \left( {3; - 1;1} \right)\) có một vectơ pháp tuyến là
A. \(\overrightarrow n = \left( { - 6;8;10} \right)\).
B. \(\overrightarrow n = \left( { - 6; - 8;10} \right)\).
C. \(\overrightarrow n = \left( {6; - 8;10} \right)\).
D. \(\overrightarrow n = \left( {6;8;10} \right)\).
Trong không gian \[Oxyz\], cho hai điểm \(M\left( {2;1;3} \right)\) và \(N\left( {4;3; - 5} \right)\). Mặt phẳng trung trực của đoạn thẳng \(MN\) có vectơ pháp tuyến là
A. \[\overrightarrow {{n_1}} = \left( {2;1;3} \right)\].
B. \[\overrightarrow {{n_2}} = \left( {4;3; - 5} \right)\].
C. \[\overrightarrow {{n_3}} = \left( {1;1; - 4} \right)\].
D. \[\overrightarrow {{n_4}} = \left( {1;1;4} \right)\].
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải