35 CÂU HỎI
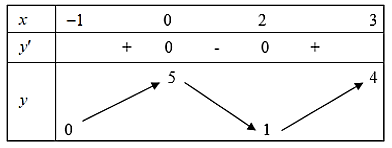
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
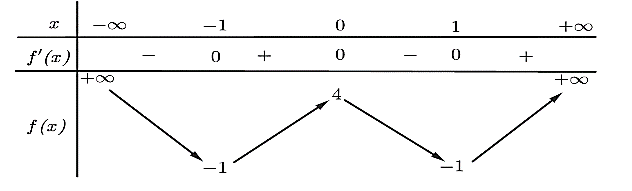
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. \[\left( { - 1;{\rm{ }}4} \right).\]
B. \[\left( { - 1; + \infty } \right).\]
C. \[\left( {0;1} \right).\]
D. \[( - 1;0).\]
Cho hàm số \[y = f\left( x \right)\] có đồ thị hàm số như hình vẽ dưới đây.
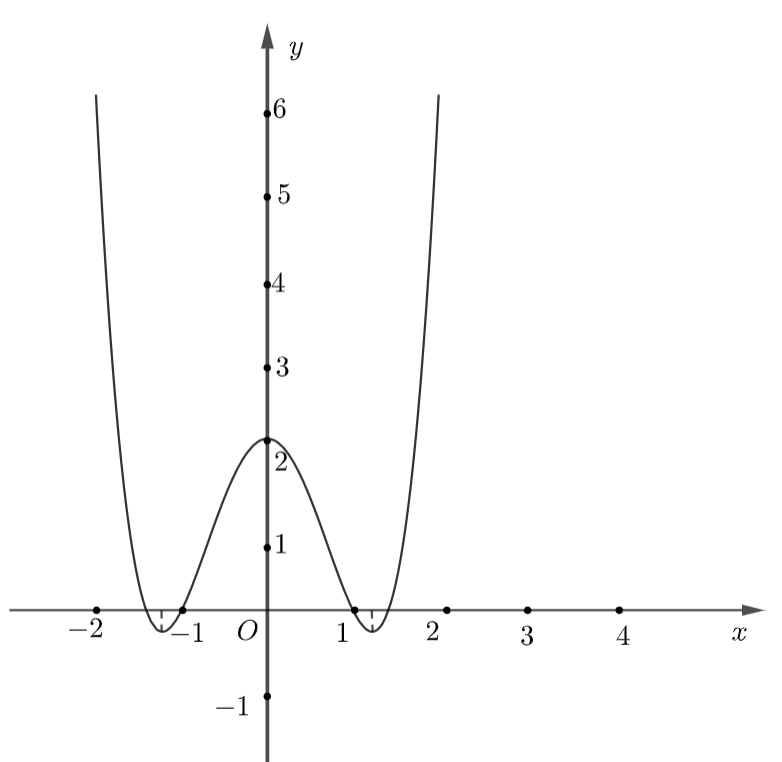
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. \[\left( { - \infty ; - 1} \right).\]
B. \[\left( { - 1;1} \right).\]
C. \[\left( {1;2} \right).\]
D. \[\left( {0;1} \right).\]
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\) và có bảng xét dấu \(f'\left( x \right)\) dưới đây:
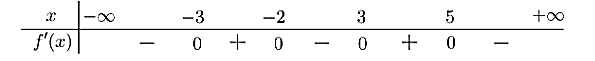
Số điểm cực trị của hàm số đã cho là:
A. \(5\).
B. \(3\).
C. \(2\).
D. \(4\).
Cho hàm số \[y = {x^3}--3{x^2} + 2\]. Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại \[x = 2\] và đạt cực tiểu tại \[x = 0\].
B. Hàm số đạt cực tiểu tại \[x = 2\] và đạt cực đại tại \[x = 0\].
C. Hàm số đạt cực đại tại \[x = - 2\] và cực tiểu tại \[x = 0\].
D. Hàm số đạt cực đại tại \[x = 0\] và cực tiểu tại \[x = - 2\].
Cho hàm số \(y = 3{x^4} - 6{x^2} + 1\). Kết luận nào sau đây là đúng?
A. ![]() .
.
B. ![]()
C. ![]()
D. ![]()
Thể tích \(V\) (đơn vị: cm3) của 1 kg nước tại nhiệt độ \(T\left( {0^\circ C \le T \le 30^\circ C} \right)\) được tính bởi công thức sau: \(V(T) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}.\) (Nguồn: J. Stewart, Calculus, Steventh Edition, Brooks/Cole, CENGAGE Learning 2012).
Hỏi thể tích \(V\left( T \right)\),\(\left( {0^\circ C \le T \le 30^\circ C} \right)\), giảm trong khoảng nhiệt độ gần với khoảng nào sau đây?
A. \(\left( {0^\circ C;30^\circ C} \right)\).
B. \(\left( {0^\circ C;4^\circ C} \right)\).
C. \(\left( {4^\circ C;30^\circ C} \right)\).
D. \(\left( {0^\circ C;26^\circ C} \right)\).
Tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số \(y = {x^3} - 3{x^2} + \left( {4 - m} \right)x\) đồng biến trên khoảng \(\left( {2; + \infty } \right)\) là:
A. \(\left( { - \infty ;1} \right]\).
B. \(\left( { - \infty ;4} \right]\).
C. \(\left( { - \infty ;1} \right)\).
D. \(\left( { - \infty ;4} \right)\).
Cho hàm số \[y = f\left( x \right)\] liên tục trên đoạn \(\left[ { - 2;3} \right]\) có đồ thị như hình vẽ dưới đây:
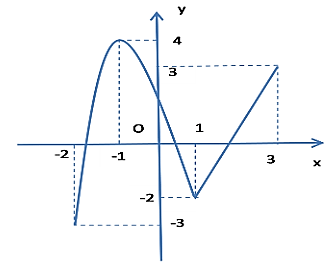
Gọi \(m,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;3} \right]\). Giá trị của \(2m - 3M\) bằng:
A. \( - 13\).
B. \( - 18\).
C. \( - 16\).
D. \( - 15\).
Cho hàm số \[y = f\left( x \right)\] liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1;3} \right]\) như hình vẽ dưới đây. Khẳng định nào sau đây là đúng?
A. \(\mathop {\max }\limits_{[ - 1;3]} \)\[f\left( x \right) = f\left( 0 \right)\].
B. \(\mathop {\max }\limits_{[ - 1;3]} \)\[f\left( x \right) = f\left( 3 \right)\].
C. \(\mathop {\max }\limits_{[ - 1;3]} \)\[f\left( x \right) = f\left( 5 \right)\].
D. \(\mathop {\max }\limits_{[ - 1;3]} \)\[f\left( x \right) = f\left( { - 1} \right)\].
Cho hàm số \(y = x - \sqrt {x - 1} \). Khẳng định nào sau đây là đúng?
A. Hàm số đạt giá trị nhỏ nhất bằng \(\frac{3}{4}\) và không có giá trị lớn nhất.
B. Hàm số đạt giá trị nhỏ nhất bằng \(\frac{3}{4}\) và giá trị lớn nhất bằng \(1\).
C. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.
D. Hàm số đạt giá trị lớn nhất tại điểm có hoành độ \(x = 1\) và giá trị lớn nhất bằng \(1\).
Giá trị lớn nhất \(M\), nhỏ nhất \(m\) của hàm số \[y = \;\frac{{2{x^2} + 3x + 3}}{{x + 1}}\] trên đoạn \(\left[ {0;2} \right]\) lần lượt là:
A. \(M = \frac{{17}}{3},m = 3.\)
B. \(M = \frac{{17}}{3},m = - 3.\)
C. \(M = 3,m = - 5.\)
D. \(M = - 3,m = - 5.\)
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để giá trị nhỏ nhất của hàm số \(y = \frac{{x + {m^2}}}{{x - 1}}\) trên đoạn \(\left[ {2;3} \right]\) bằng \(14\)?
A. \(2\).
B. \(1\).
C. \(0\).
D. \(4\).
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ:
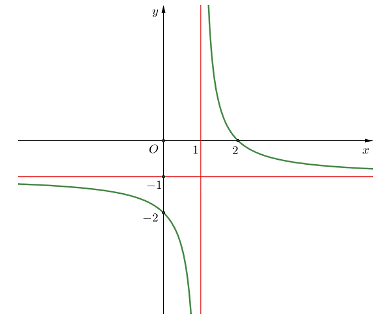
Đồ thị hàm số đã cho có đường tiệm cận đứng là đường thẳng:
A. \(x = 1\).
B. \(x = - 1\).
C. \(x = 0\).
D. \(y = - 1\).
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ.
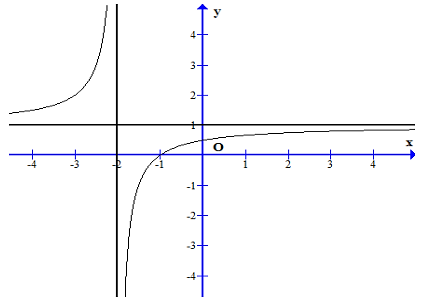
Phương trình đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số là:
A. Tiệm cận đứng \(x = - 2\), tiệm cận ngang \(y = 1\).
B. Tiệm cận đứng \(x = 2\), tiệm cận ngang \(y = - 1\).
C. Tiệm cận đứng \(x = 1\), tiệm cận ngang \(y = - 2\).
D. Tiệm cận đứng \(x = - 1\), tiệm cận ngang \(y = 2\).
Đường thẳng \(y = 2x - 1\) là tiệm cận xiên của đồ thị hàm số nào sau đây?
A. \(y = \frac{{2{x^2} - 3x + 5}}{{x - 1}}\).
B. \(y = \frac{{ - 2{x^2} - 3x + 5}}{{x + 1}}\).
C. \(y = \frac{{{x^2} - 3x + 5}}{{x - 2}}\).
D. \(y = \frac{{ - 2{x^2} - 3x + 5}}{{ - x + 1}}\).
Đồ thị hàm số \(y = \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}}\) có bao nhiêu đường tiệm cận?
A. \(2\).
B. \(3\).
C. \(4\).
D. \(1\).
Cho hàm số \(y = \frac{{x - 2}}{{x + 2}}\) có đồ thị \[\left( C \right)\]. Tìm tọa độ giao điểm \(I\) của hai đường tiệm cận của đồ thị \[\left( C \right)\].
A. \(I\left( { - 2;2} \right)\).
B. \(I\left( { - 2; - 2} \right)\).
C. \(I\left( {2;1} \right)\).
D. \(I\left( { - 2;1} \right)\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\).
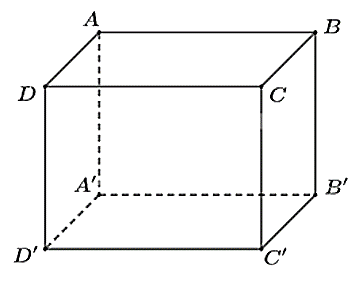
Mệnh đề nào sau đây là sai?
A. \(\overrightarrow {AB} = \overrightarrow {A'B'} \).
B. \(\overrightarrow {AD} = \overrightarrow {B'C'} \).
C. \(\overrightarrow {CD} = \overrightarrow {A'B'} \).
D. \(\overrightarrow {BC} = \overrightarrow {A'D'} \).
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(AB,CD\) và \(G\) là trung điểm \(MN\). Trong các khẳng định sau, khẳng định nào sai?
A. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \) với \(O\) là điểm bất kì.
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {DG} \).
C. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
D. \(\overrightarrow {GM} + \overrightarrow {GN} = \overrightarrow 0 \).
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ đều khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây là đúng?
A. \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow a ,\overrightarrow b } \right)\).
B. \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
C. \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\)
D. \(\overrightarrow a .\overrightarrow b = - 1.\)
Cho tứ diện \(ABCD\) có \(AB = AC = AD\) và \(\widehat {BAC} = \widehat {BAD} = 60^\circ \). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \)?
A. \(120^\circ \).
B. \(60^\circ \).
C. \(45^\circ \).
D. \(90^\circ \).
Cho tứ diện \(ABCD\) có \(AB = AC = AD\) và \(\widehat {BAC} = \widehat {BAD} = 60^\circ \), \(\widehat {CAD} = 90^\circ \). Gọi \(I\) và \(J\) lần lượt là trung điểm của \(AB\) và \(CD\). Hãy xác định góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \)?
A. \(120^\circ \).
B. \(60^\circ \).
C. \(45^\circ \).
D. \(90^\circ \).
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc \(100^\circ \) và có độ lớn lần lượt là \(25N\) và \(12N\). Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn \(4N\). Tính độ lớn của hợp lực của ba lực trên (Làm tròn kết quả đến hàng đơn vị).
A. \(26N\).
B. \(25N\).
C. \(41N\).
D. \(72N\).
Trong không gian với hệ trục \[Oxyz\], cho \(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \) là:
A. \(\left( { - 1;2; - 3} \right)\).
B. \(\left( {2; - 3; - 1} \right)\).
C. \(\left( {2; - 1; - 3} \right)\).
D. \(\left( { - 3;2; - 1} \right)\).
Trong không gian \[Oxyz\], hình chiếu vuông góc của điểm \(A\left( {3;5;2} \right)\) trên trục \(Ox\) có tọa độ là:
A. \(\left( {0;5;2} \right)\).
B. \(\left( {0;5;0} \right)\).
C. \(\left( {3;0;0} \right)\).
D. \(\left( {0;0;2} \right)\).
Trong không gian \[Oxyz\], tìm tọa độ điểm đối xứng của \(A\left( {1;2; - 3} \right)\) qua mặt phẳng \[\left( {Oyz} \right)\] là:
A. \(\left( {0;2;3} \right)\).
B. \(\left( { - 1; - 2; - 3} \right)\).
C. \(\left( { - 1;2; - 3} \right)\).
D. \(\left( { - 1;2; - 3} \right)\).
Trong không gian với hệ trục \[Oxyz\], cho hình hộp \(ABCD.A'B'C'D'\), biết rằng \[A( - 3;0;0),{\rm{ }}B\left( {0;2;0} \right),{\rm{ }}D\left( {0;0;1} \right),{\rm{ }}A'\left( {1;2;3} \right)\]. Tìm tọa độ điểm \[C'\].
A.\(\left( {10;4;4} \right)\).
B. \(\left( { - 13;4;4} \right)\).
C. \(\left( {13;4;4} \right)\).
D. \(\left( {7;4;4} \right)\).
Trong không gian với hệ trục \[Oxyz\], cho tam giác \(ABC\) với \[A\left( {8;9;2} \right)\], \[B\left( {3;5;1} \right),\]\[C\left( {11;10;4} \right).\] Số đo góc \(\widehat {BAC}\) của tam giác \(ABC\) đó là:
A. \(150^\circ \).
B. \(60^\circ \).
C. \(120^\circ \).
D. \(30^\circ \).
Trong không gian với hệ trục tọa độ \[Oxyz\], điểm thuộc trục \(Ox\)và cách đều hai điểm \(A\left( {4;2; - 1} \right)\) và \(B\left( {2;1;0} \right)\) là:
A. \(M\left( { - 4;0;0} \right)\).
B. \(M\left( {4;0;0} \right)\).
C. \(M\left( {5;0;0} \right)\).
D. \(M\left( { - 5;0;0} \right)\).
Trong không gian \[Oxyz\], cho hai điểm \(A\left( {1;2;1} \right)\), \(B\left( {2; - 1;3} \right)\). Tìm điểm \(M\) trên mặt phẳng \[\left( {Oxy} \right)\] sao cho \[M{A^2}--2M{B^2}\] lớn nhất.
A.\(M\left( {3; - 4;0} \right)\).
B. \(M\left( {\frac{3}{2};\frac{1}{2};0} \right)\).
C. \(M\left( {0;0;5} \right)\).
D. \(M\left( {\frac{1}{2};\frac{{ - 3}}{2};0} \right)\).
Trong không gian \[Oxyz\], cho hai vectơ \(\overrightarrow u = (1; - 4;0)\) và \(\overrightarrow v = ( - 1; - 2;1)\). Vectơ \(\overrightarrow u + 3\overrightarrow v \) có tọa độ là:
A.\(\left( { - 2; - 10;3} \right)\).
B.\(\left( { - 2; - 6;3} \right)\).
C.\(\left( { - 4;8;4} \right)\).
D.\(\left( { - 2; - 10; - 3} \right)\).
Trong không gian \[Oxyz\], cho \(\overrightarrow u = \left( { - 1;1;0} \right)\), \(\overrightarrow v = (0; - 1;0)\), góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là:
A. \(120^\circ \).
B. \(60^\circ \).
C. \(150^\circ \).
D. \(135^\circ \).
Trong không gian \[Oxyz\], cho hai vectơ \(\overrightarrow a = \left( {2;1; - 1} \right)\),\(\overrightarrow b = \left( {1;3;m} \right)\). Tìm \(m\) để \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \).
A. \(m = - 5\).
B. \(m = 5\).
C. \(m = 1\).
D. \(m = - 2\).
Trong không gian \[Oxyz\], cho ba điểm \(A(1; - 2;3)\),\(B( - 1;2;5)\),\(C(0;0;1)\).Tìm tọa độ trọng tâm \(G\) của tam giác \(ABC\).
A.\(\left( {5;9;13} \right)\).
B.\(\left( {0;0;3} \right)\).
C.\(\left( {0;0;9} \right)\).
D.\(\left( { - 1;0;3} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \(B(1;2 - 3)\), \(C(7;4; - 2)\). Nếu điểm \(E\) thỏa mãn đẳng thức \(\overrightarrow {CE} = 2\overrightarrow {EB} \) thì tọa độ điểm \(E\) là:
A.\(\left( {3;\frac{8}{3}; - \frac{8}{3}} \right)\).
B.\(\left( {\frac{8}{3};3; - \frac{8}{3}} \right)\).
C.\(\left( {3;3; - \frac{8}{3}} \right)\).
D.\(\left( {1;2;\frac{1}{3}} \right)\).

