12 CÂU HỎI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] có đồ thị là đường cong như hình dưới đây.
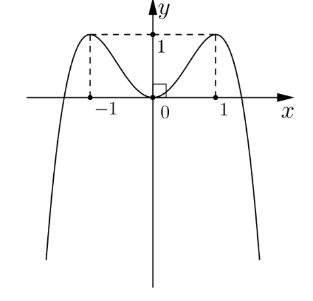
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. \[\left( { - 1;0} \right)\].
B. \[\left( { - \infty ; - 1} \right)\].
C. \[\left( {0;1} \right)\].
D. \[\left( {0; + \infty } \right)\].
Hàm số đã cho có bao nhiêu điểm cực đại?
A. \[0\].
B. \[1\].
C. \[2\].
D. \[3\].
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên trên \(\left[ { - 5;7} \right)\) như sau:
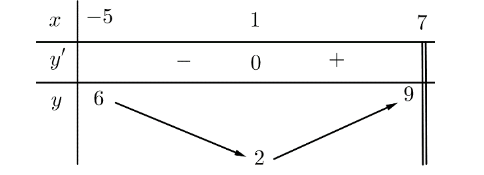
Mệnh đề nào dưới đây là đúng?
A. \(\mathop {\min }\limits_{\left[ { - 5;7} \right)} f\left( x \right) = 6\).
B. \(\mathop {\min }\limits_{\left[ { - 5;7} \right)} f\left( x \right) = 2\).
C. \(\mathop {\max }\limits_{\left[ { - 5;7} \right)} f\left( x \right) = 9\).
D. \(\mathop {\max }\limits_{\left[ { - 5;7} \right)} f\left( x \right) = 6\).
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ dưới đây.
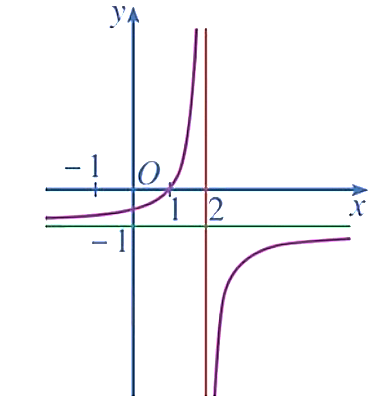
Đồ thị hàm số đã cho có tiệm cận đứng và tiệm cận ngang lần lượt là các đường thẳng:
A. \(x = 2\); \(y = - 2\).
B. \(x = 1\); \(y = 2\).
C. \(x = - 1\); \(y = 2\).
D. \(x = 2\); \(y = - 1\).
Cho hình hộp \(ABCD.A'B'C'D'\). Vectơ \(\overrightarrow v = \overrightarrow {B'A'} + \overrightarrow {B'C'} + \overrightarrow {B'B} \) bằng vectơ nào dưới đây?
A. \(\overrightarrow {DB'} \).
B. \(\overrightarrow {B'D'} \).
C. \(\overrightarrow {BD'} \).
D. \(\overrightarrow {B'D} \).
Trong không gian với hệ tọa độ \[Oxyz\], cho vectơ \(\overrightarrow u = 2\overrightarrow i + 3\overrightarrow j - 7\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow u \) là:
A. \(\left( {2;3;7} \right)\).
B. \(\left( { - 2; - 3;7} \right)\).
C. \(\left( {2;3; - 7} \right)\).
D. \(\left( { - 7;3;2} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho vectơ \(\overrightarrow u = \left( {1; - 6;2} \right)\) và điểm \(A\). Biết \(\overrightarrow {OA} = \overrightarrow u \). Tọa độ của điểm \(A\) là:
A. \(\left( {1; - 6;2} \right)\).
B. \(\left( {0; - 6;2} \right)\).
C. \(\left( {2; - 6;1} \right)\).
D. \(\left( {1;6;2} \right)\).
Cho hàm số \(y = - {x^3} + 3{x^2} - 6x\). Khẳng định nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)
B. Hàm số đã cho nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
C. Hàm số đã cho có một cực trị.
D. Hàm số đã cho có hai cực trị.
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^4} - 12{x^2} - 1\) trên đoạn \(\left[ {0;\,9} \right]\) bằng
A. \( - 28\).
B. \( - 1\).
C. \( - 36\).
D. \( - 37\).
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - x + 3}}{{2x + 1}}\) là đường thẳng:
A. \(y = x - 1\).
B. \(y = 2x + 1\).
C. \(y = 2x - 1\).
D. \(y = x + 1\).
Đường cong trong hình dưới đây là đồ thị của hàm số nào trong bốn hàm số ở các phương án A, B, C, D.
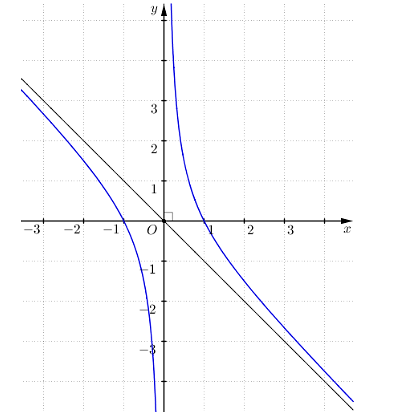
A. \(y = \frac{{ - {x^2} + 1}}{x}\).
B. \(y = \frac{{ - 2x + 1}}{{2x + 2}}\).
C. \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\).
D. \(y = {x^3} - 3{x^2}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\sqrt 2 \). Góc giữa hai vectơ \(\overrightarrow {AB'} \) và \(\overrightarrow {A'C'} \) bằng:
A. \(30^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(90^\circ \).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
