12 CÂU HỎI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
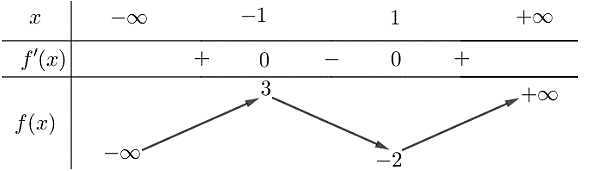
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. \[\left( { - 1; + \infty } \right)\].
B. \[\left( {1; + \infty } \right)\].
C. \[\left( { - 1;1} \right)\].
D. \[\left( { - \infty ;1} \right)\].
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
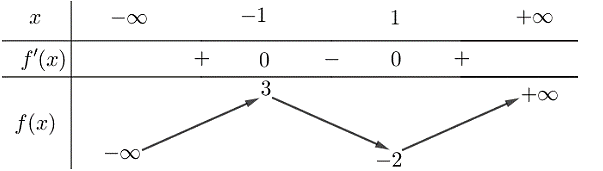
Giá trị cực tiểu của hàm số đã cho bằng
A. \[ - 1\].
B. \[1\].
C. \[3\].
D. \[ - 2\].
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên \(\mathbb{R}\) có đồ thị hàm số như hình vẽ dưới đây.
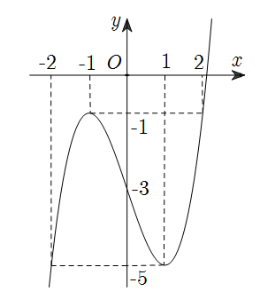
Giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số đã cho trên đoạn \(\left[ { - 2;2} \right]\) lần lượt là:
A. \(m = - 5,M = - 1\).
B. \(m = - 2,M = 2\).
C. \(m = - 1,M = 0\).
D. \(m = - 5,M = 0\).
Cho hàm số \[y = f\left( x \right)\] có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\) và \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 2\). Phát biểu nào dưới đây là đúng?
A. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng \(x = 2\) và \(x = - 2\).
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng \(y = 2\) và \(y = - 2\).
Cho tứ diện \(ABCD\). Có bao nhiêu vectơ khác vectơ \(\overrightarrow 0 \) mà mỗi vectơ có điểm đầu và điểm cuối là hai đỉnh của tứ diện \(ABCD\)?
A. \(4\).
B. \(8\).
C. \(10\).
D. \(12\).
Trong không gian với hệ tọa độ \[Oxyz\], cho điểm \(M\left( { - 2; - 5;7} \right)\). Tọa độ của vectơ \(\overrightarrow {OM} \) là:
A. \(\left( { - 2; - 5;7} \right)\).
B. \(\left( { - 2;5;7} \right)\).
C. \(\left( {2;5;7} \right)\).
D. \(\left( {2;5; - 7} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho vectơ \(\overrightarrow u = - 3\overrightarrow i + \overrightarrow j - 8\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow u \) là:
A. \(\left( {3;1;8} \right)\).
B. \(\left( {3; - 1;8} \right)\).
C. \(\left( { - 3;1; - 8} \right)\).
D. \(\left( { - 8;1; - 3} \right)\).
Cho hàm số \(y = \frac{{{x^2} + 3}}{{x - 1}}\). Khẳng định nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng \(\left( {1; + \infty } \right)\)
B. Hàm số đã cho nghịch biến trên khoảng \(\left( { - 1;3} \right)\).
C. Hàm số đã cho đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\).
D. Hàm số đã cho nghịch biến trên khoảng \(\left( {1;3} \right)\).
Giá trị lớn nhất của hàm số \(y = 2\cos x - \frac{4}{3}{\cos ^3}x\) trên đoạn \(\left[ {0;\,\pi } \right]\) bằng
A. \(\frac{2}{3}\).
B. \(\frac{{10}}{3}\).
C. \(\frac{{2\sqrt 2 }}{3}\).
D. \(0\).
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 3x + 6}}{{x + 2}}\) là đường thẳng:
A. \(y = x - 5\).
B. \(y = x + 5\).
C. \(y = x + 2\).
D. \(y = x - 3\).
Cho hàm số \(y = \frac{{ax - b}}{{x - 1}}\) có đồ thị như hình vẽ dưới đây.
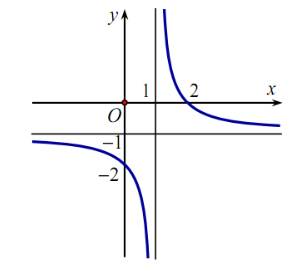
Khẳng định nào sau đây là đúng?
A. \(b < a < 0\).
B. \(a < b < 0\).
C. \(b > a\) và \(a < 0\).
D. \(a < 0 < b\).
Cho tứ diện \(ABCD\) và điểm \(G\) thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \) (\(G\) là trọng tâm của tứ diện). Gọi \({G_0}\) là giao điểm của \(GA\) và mặt phẳng \(\left( {BCD} \right)\). Trong các khẳng định sau, khẳng định nào đúng?
A. \(\overrightarrow {GA} = - 2\overrightarrow {{G_0}G} \).
B. \(\overrightarrow {GA} = 4\overrightarrow {{G_0}G} \).
C. \(\overrightarrow {GA} = 3\overrightarrow {{G_0}G} \).
D. \(\overrightarrow {GA} = 2\overrightarrow {{G_0}G} \).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải