Quiz

Đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 2

Admin32 câu hỏiToánLớp 10

Bắt đầu ngay

32 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Trong các phát biểu sau, phát biểu nào không phải là mệnh đề?

A. 2 là số nguyên âm;

B. Bạn có thích học môn Toán không?;

C. 13 là số nguyên tố;

D. Số 15 chia hết cho 2.

2. Nhiều lựa chọn

Trong các tập hợp sau, tập hợp nào là con của tập hợp A = {1; 2; 3; 4; 5}?

A. A₁ = {1; 6};

B. A₂ = {0; 1; 3};

C. A₃ = {4; 5};

D. A₄ = {0}.

3. Nhiều lựa chọn

Cho các tập hợp A = {x ∈ ℝ | – 5 ≤ x < 1} và B = {x ∈ ℝ | – 3 < x ≤ 3}. Tìm tập hợp A ∪ B.

A. A ∪ B = [– 5; 1);

B. A ∪ B = [– 5; 3];

C. A ∪ B = (– 3; 1);

D. A ∪ B = (– 3; 3].

4. Nhiều lựa chọn

Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?

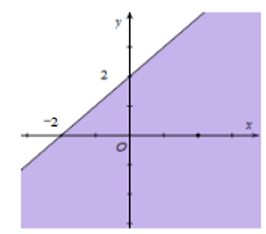
Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau? (ảnh 1)

A. x + 2y > 1;

B. 2x + y > 1;

C. 2x + y < 1;

D. 2x – y > 1.

5. Nhiều lựa chọn

Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình $\{\begin{cases} x + y - 2 \leq 0 \\ 2 x - 3 y + 2 > 0 \end{cases}$ ?

A. (0; 0);

B. (1; 1);

C. (– 1; 1);

D. (– 1; – 1).

6. Nhiều lựa chọn

Mệnh đề nào sau đây đúng?

A. sin (180° – α) = – sin α;

B. cos (180° – α) = – cos α;

C. tan (180° – α) = tan α;

D. cot (180° – α) = cot α);

7. Nhiều lựa chọn

Tam giác ABC có BC = 1, AC = 3, C=60 $°$ . Tính độ dài cạnh AB.

A. $\sqrt{13}$ ;

B. $\frac{\sqrt{46}}{2}$

C. $\frac{\sqrt{34}}{2}$

D. $\sqrt{7}$

8. Nhiều lựa chọn

Cho hai mệnh đề P: “x là số chẵn” và Q: “x chia hết cho 2”.

Phát biểu mệnh đề P kéo theo Q.

A. Hoặc x là số chẵn hoặc x chia hết cho 2;

B. Nếu x là số chẵn thì x chia hết cho 2;

C. Nếu x chia hết cho 2 thì x là số chẵn;

D. x là số chẵn và x chia hết cho 2.

9. Nhiều lựa chọn

Trong các cặp số sau đây: (– 5; 0); (– 2; 1); (– 1; 3); (– 7; 0). Có bao nhiêu cặp số là nghiệm của bất phương trình x – 4y + 5 ≥ 0?

A. 0;

B. 1;

C. 3;

D. 4.

10. Nhiều lựa chọn

Giá trị của biểu thức P = sin30°.cos15° + sin150°.cos165°là

A. 0;

B. 1;

C. – 1;

D. 0,5.

11. Nhiều lựa chọn

Mệnh đề phủ định của mệnh đề P: “∃x, x² + 2x + 3 là số chính phương” là:

A. ∀x, x² + 2x + 3 không là số chính phương;

B. ∃x, x² + 2x + 3 là số nguyên tố;

C. ∀x, x² + 2x + 3 là hợp số;

D. ∃x, x² + 2x + 3 là số thực.

12. Nhiều lựa chọn

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn ?

A. 2x² + 1 ≥ y + 2x²;

B. 2x – 6y + 5 < 2x – 6y + 3;

C. 4x² < 2x + 5y – 6;

D. 2x³ + 1 ≥ y + 2x².

13. Nhiều lựa chọn

Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Khẳng định nào dưới đây đúng?

A. a²= b² + c² + 2bcsinA;

B. a² = b² + c² – 2bccosA;

C. a² = b² + c²– 2acsinA;

D. a² = b² + c² + 2abcosA.

14. Nhiều lựa chọn

Cho tập hợp D = {x ∈ ℕ^* | x(x – 2)(x – 3) = 0}.

Viết lại tập hợp D dưới dạng liệt kê các phần tử của tập hợp đó

A. D = {0; 1; 2};

B. D = {2; 3};

C. D = {0; 2; 3};

D. D = {1; 2}.

15. Nhiều lựa chọn

Hệ nào là hệ bất phương trình bậc nhất hai ẩn trong các hệ sau?

A. $\{\begin{cases} x^{2} + 7 \geq 0 \\ x - y < 0 \end{cases}$

B. $\{\begin{cases} 2 x^{3} - y - 1 > 0 \\ x - 2 > 0 \\ x + 5 y = 4 \end{cases}$

C. $\{\begin{cases} 3 x + 2 y > 2 - y \\ 3 x - y < 4 y \end{cases}$

D. $\{\begin{cases} 7 x - y < 1 \\ x + 6 y = 4 y \end{cases}$

16. Nhiều lựa chọn

Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. S là diện tích và p là nửa chu vi tam giác. R là bán kính đường tròn ngoại tiếp và r là bán kính đường tròn nội tiếp tam giác. Công thức nào sau đây sai?

A. S = $\frac{a b c}{4 R}$ ;

B. S = pr ;

C. S = $\sqrt{p (p + a) (p + b) (p + c)}$ ;

D. S = $\frac{1}{2}$ bcsinA.

17. Nhiều lựa chọn

Cho $μ = 45 °$ , chọn đáp án SAI trong các đáp án dưới đây?

A. sin A = $\frac{\sqrt{3}}{2}$ ;

B. cos A = $\frac{\sqrt{2}}{2}$ ;

C. tan A = 1;

D. cot A = 1.

18. Nhiều lựa chọn

Cho tam giác ABC có BC = a, AC = b, AB = c, có R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và h_c là độ dài đường cao xuất phát từ đỉnh C. Chọn mệnh đề sai.

A. S_ABC = absinC;

B. S_ABC = $\frac{1}{2} . c . h_{c}$ ;

C. S_ABC = pr;

D. S_ABC= $\frac{a b c}{4 R}$ .

19. Nhiều lựa chọn

Cho hệ bất phương trình $\{\begin{cases} 7 x - 5 y + 2 \geq 0 \\ y - 2 x - 5 < 0 \end{cases}$ . Trong các điểm sau đây, điểm không thuộc miền nghiệm của hệ bất phương trình là

A. O(0; 0);

B. A(2; 3);

C. B(5; 4);

D. C(−2; −2) .

20. Nhiều lựa chọn

Tam giác ABC có B= 60°, C= 45° và AB = 7. Tính độ dài cạnh AC.

A. AC = $\frac{5 \sqrt{6}}{2}$ ;

B. AC = $\frac{7 \sqrt{6}}{2}$ ;

C. AC = 7 $\sqrt{2}$ ;

D. AC = 10.

21. Nhiều lựa chọn

Cho mệnh đề: “Nếu a + b < 2 thì một trong hai số a và b nhỏ hơn 1”. Phát biểu mệnh đề trên bằng cách sử dụng khái niệm “điều kiện đủ”.

A. a + b < 2 là điều kiện đủ để một trong hai số a và b nhỏ hơn 1;

B. Một trong hai số a và b nhỏ hơn 1 là điều kiện đủ để a + b < 2;

C. Từ a + b < 2 suy ra một trong hai số a và b nhỏ hơn 1;

D. Tất cả các câu trên đều đúng.

22. Nhiều lựa chọn

Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào?

Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào? (ảnh 1)

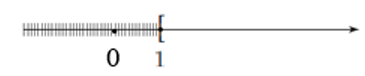
A. (0; 1);

B. (1; + ∞);

C. [1; + ∞);

D. (0; 1].

23. Nhiều lựa chọn

Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?

A. sin α = sin β;

B. cos α = – cos β;

C. tan α = – tan β;

D. cot α = cot β.

24. Nhiều lựa chọn

Cho hai tập hợp A = {1; 2; 4; 6} và B = {1; 2; 3; 4; 5; 6; 7; 8}. Xác định tập C_BA.

A. C_BA = {1; 2; 4; 6};

B. C_BA = {4; 6};

C. C_BA = {3; 5; 7; 8};

D. C_BA = {2; 6; 7; 8}.

25. Nhiều lựa chọn

Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)?

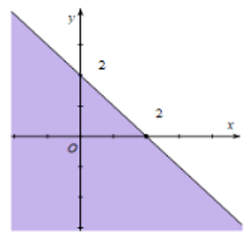
Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)? (ảnh 1)

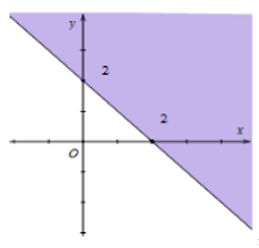
Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)? (ảnh 2)

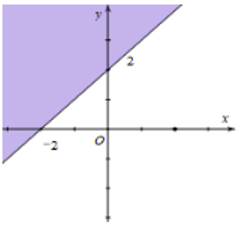
Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)? (ảnh 3)

Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)? (ảnh 4)

26. Nhiều lựa chọn

Tam giác ABC có AB = 4, BC = 6, AC = $2 \sqrt{7}$ . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM.

A. AM = 4 $\sqrt{2}$ ;

B. AM = 3;

C. AM = 2 $\sqrt{3}$ ;

D. AM = 3 $\sqrt{2}$ .

27. Nhiều lựa chọn

Cho góc α (0° < α < 180°) thỏa mãn sin α + cos α = 1. Giá trị của tan α là

A. 0;

B. 1;

C. – 1;

D. Không tồn tại.

28. Nhiều lựa chọn

Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ bên (kể cả đường thẳng d)?

Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ bên (kể cả đường thẳng d)? (ảnh 1)

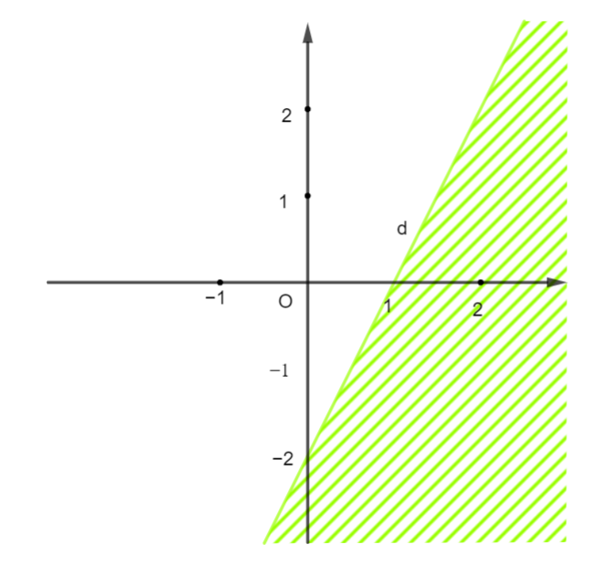
A. 2x − y ≤ 2;

B. 2x − 3y ≤ 0;

C. 2x + y < 2;

D. 2x − y > 2.

29. Nhiều lựa chọn

Cho góc α (0° < α < 180°) thỏa mãn tan α = $\frac{1}{3}$ .

Giá trị của biểu thức P = $\frac{\sin α + 3 \sin α}{2 \sin α - 5 \sin α}$ là

A. $\frac{13}{10}$

B. $- \frac{13}{10}$

C. $- \frac{10}{13}$

D. $\frac{10}{13}$

30. Nhiều lựa chọn

Một ca nô xuất phát từ cảng A, chạy theo hướng đông với vận tốc 50 km/h. Cùng lúc đó, một tàu cá, xuất phát từ A, chạy theo hướng N30°E với vận tốc 40 km/h. Sau 3 giờ, hai tàu cách nhau bao nhiêu kilômét?

A. 135,7 km;

B. 110 km;

C. 137,5 km;

D. 237,5 km.

31. Nhiều lựa chọn

Cho bất phương trình 2x − 3y < 12 (với x, y Î ℝ). Điều nào sau đây là sai ?

A. Đây là bất phương trình bậc nhất hai ẩn;

B. Cặp số (5; 3) là nghiệm của bất phương trình;

C. Cặp số (9; 2) là nghiệm của bất phương trình;

D. Cặp số (9; 3) là nghiệm của bất phương trình.

32. Nhiều lựa chọn

Một công ty nhập về 1 tấn gỗ để sản xuất bàn và ghế. Biết một cái bàn cần 30 kg gỗ và một cái ghế cần 15 kg gỗ. Gọi x và y lần lượt là số bàn và số ghế mà công ty sản xuất. Viết bất phương trình bậc nhất hai ẩn x, y sao cho lượng bàn ghế mà công ty sản xuất không vượt quá 1 tấn gỗ ?

A. 30x + 50y < 1 000;

B. 30x + 50y ≤ 1 000;

C. 30x + 50y > 1 000;

D. 30x + 50y ≥ 1 000.

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube