35 CÂU HỎI
Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x
A. x + 3y = 7;
B. x2 + y2 = 5;
C. \(y = \sqrt {{x^2} - 2} \);
D. \(y = \frac{2}{x}\).
Cho hàm số dưới dạng bảng như sau:
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
1 |
3 |
5 |
7 |
9 |
Giá trị của hàm số y tại x = 3 là
A. 2
B. 3
C. 5
D. 7
Cho hàm số y = f(x) có đồ thị như hình dưới.
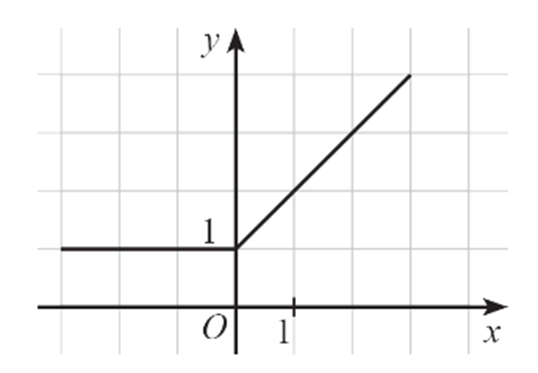
Hàm số trên đồng biến trên khoảng
A. (0; 1);
B. (1; + ∞);
C. (0; + ∞);
D. (– ∞; 0).
Hàm số \(y = \frac{{x + 2}}{{{x^2} - 3x + 2}}\) có tập xác định là
A. (1; 2);
B. [1; 2];
C. {1; 2};
D. ℝ \ {1; 2}.
Cho hàm số \(y = 2\sqrt {{x^2} - 5x} \). Giá trị của hàm số tại x = 10 là
A. 20;
B. \(10\sqrt 2 \);
C. \[2\sqrt {10} \];
D. Không tồn tại.
Trong các hàm số sau, hàm số nào không phải là hàm số bậc hai?
A. y = x2 – 5x + 3;
B. y = 1 – 2x2 + 4x;
C. y = x(x2 + x + 1);
D. y = 7 – x2.
Cho hàm số bậc hai y = 2x2 + 3x – 8. Hoành độ đỉnh của đồ thị hàm số bậc hai này là
A. \( - \frac{3}{4}\);
B. \(\frac{3}{4}\);
C. \(\frac{3}{2}\);
D. \( - \frac{3}{2}\).
Hàm số bậc hai y = 2 – 3x2 + 4x có hệ số tự do là
A. 2;
B. – 3;
C. 4;
D. – 2.
Cho hàm số bậc hai f(x) = 2x2 – 8x + 7. Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (– ∞; 2), nghịch biến trên khoảng (2; + ∞);
B. Hàm số đồng biến trên khoảng (– ∞; 4), nghịch biến trên khoảng (4; + ∞);
C. Hàm số đồng biến trên khoảng (4; + ∞), nghịch biến trên khoảng (– ∞; 4);
D. Hàm số đồng biến trên khoảng (2; + ∞), nghịch biến trên khoảng (– ∞; 2).
Xác định parabol y = ax2 + c, biết rằng parabol này đi qua hai điểm A(1; 1) và B(2; – 2).
A. y = – x2 + 2;
B. y = x2 + 2;
C. y = 2x2 – 1;
D. y = 2x2 + 1.
Tìm khẳng định đúng trong các khẳng định sau.
A. f(x) = 3x2 + x – 4 là tam thức bậc hai;
B. f(x) = 3x – 5 là tam thức bậc hai;
C. f(x) = 2x3 + 3x – 2 là tam thức bậc hai;
D. f(x) = (x2)2 – x2 + 3 là tam thức bậc hai.
Cho hàm số f(x) = ax2 + bx + c, (a ≠ 0) và ∆ = b2 – 4ac. Cho biết dấu của ∆ khi f(x) luôn cùng dấu với hệ số a với mọi x ∈ ℝ.
A. ∆ ≤ 0;
B. ∆ = 0;
C. ∆ > 0;
D. ∆ < 0.
Cho tam thức f(x) = x2 – 8x + 16. Khẳng định nào sau đây là đúng?
A. Phương trình f(x) = 0 vô nghiệm;
B. f(x) > 0 với mọi x ∈ ℝ;
C. f(x) ≥ 0 với mọi x ∈ ℝ;
D. f(x) < 0 khi x < 4.
Trong các phát biểu sau, phát biểu nào sai?
A. x2 – 3x + 2 > 0 khi x ∈ (– ∞; 1) ∪ (2; + ∞);
B. x2 – 3x + 2 ≤ 0 khi x ∈ [1; 2];
C. x2 – 3x + 2 < 0 khi x ∈ [1; 2);
D. x2 – 3x + 2 ≥ 0 khi x ∈ (– ∞; 1] ∪ [2; + ∞).
Tập nghiệm của bất phương trình x2 – 7x + 10 < 0 là
A. S = (– ∞; 2] ∪ [5; + ∞);
B. S = (– ∞; 2) ∪ (5; + ∞);
C. S = [2; 5];
D. S = (2; 5).
Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\] là tập nghiệm của phương trình ax2 + bx + c = (dx + e)2;
B. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\] là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình dx + e ≥ 0;
C. Mọi nghiệm của phương trình ax2 + bx + c = (dx + e)2 đều là nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\];
D. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = dx + e\] là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình ax2 + bx + c ≥ 0.
Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập nghiệm của phương trình ax2 + bx + c = dx2 + ex + f;
B. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập nghiệm của phương trình (ax2 + bx + c)2 = (dx2 + ex + f)2;
C. Mọi nghiệm của phương trình ax2 + bx + c = dx2 + ex + f đều là nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \];
D. Tập nghiệm của phương trình \[\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \] là tập hợp các nghiệm của phương trình ax2 + bx + c = dx2 + ex + f thỏa mãn bất phương trình ax2 + bx + c ≥ 0 (hoặc dx2 + ex + f ≥ 0).
Số nghiệm của phương trình \(\sqrt {4 - 3{x^2}} = 2x - 1\) là
A. 0
B. 1
C. 2
D. 3
Giá trị nào sau đây là một nghiệm của phương trình\(\sqrt {3{x^2} - 6x + 1} = \sqrt {{x^2} - 3} \)?
A. 2;
B. 4;
C. 12;
D. 20.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 3 = 0. Vectơ pháp tuyến của đường thẳng d là
A. \(\overrightarrow n = \left( {1;\,\, - 2} \right)\);
B. \(\overrightarrow n = \left( {1;\,\,2} \right)\);
C. \(\overrightarrow n = \left( {2;\,\, - 1} \right)\);
D. \(\overrightarrow n = \left( {2;\,\,1} \right)\).
Điểm nào dưới đây thuộc đường thẳng d: 3x – 2y + 4 = 0?
A. A(1; 2);
B. B(0; 2);
C. C(2; 0);
D. D(2; 1).
Phương trình tham số của đường thẳng ∆ đi qua điểm A(3; 1) và nhận \(\overrightarrow u = \left( {3;\,\, - 1} \right)\) làm vectơ chỉ phương là
A. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = 1 - t\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = 1 + t\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 + t\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 - t\end{array} \right.\).
Phương trình tổng quát của đường thẳng d đi qua điểm A(2; – 2) và nhận \(\overrightarrow n = \left( {1;\,\,3} \right)\) làm vectơ pháp tuyến là
A. x – y + 2 = 0;
B. – 3x + y + 4 = 0;
C. x – 3y + 4 = 0;
D. x + 3y + 4 = 0.
Cho đường thẳng d có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng d là
A. 2x + y – 1 = 0;
B. – 2x + y – 1 = 0;
C. x + 2y + 1 = 0;
D. 2x + 3y – 1 = 0.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(– 2; 3) và B(4; – 1). Phương trình nào sau đây là phương trình đường thẳng AB?
A. x + y – 3 = 0;
B. y = 2x + 2;
C. \(\frac{{x - 4}}{6} = \frac{{y - 1}}{{ - 4}}\);
D. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 - 2t\end{array} \right.\).
Trong mặt phẳng tọa độ, xét hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0.
và hệ phương trình: \[\left\{ \begin{array}{l}{a_1}x + {b_1}y + {c_1} = 0\\{a_2}x + {b_2}y + {c_2} = 0\end{array} \right.\] (*).
Khi đó, ∆1 song song với ∆2 khi và chỉ khi
A. hệ (*) có vô số nghiệm;
B. hệ (*) vô nghiệm;
C. hệ (*) có nghiệm duy nhất;
D. hệ (*) có hai nghiệm.
Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0. Khoảng cách từ điểm M đến đường thẳng ∆, kí hiệu là d(M, ∆), được tính bởi công thức
A. \[d\left( {M,\,\,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\];
B. \[d\left( {M,\,\,\Delta } \right) = \frac{{a{x_0} + b{y_0} + c}}{{\sqrt {{a^2} + {b^2}} }}\];
C. \[d\left( {M,\,\,\Delta } \right) = \frac{{a{x_0} + b{y_0} + c}}{{\sqrt {x_0^2 + y_0^2} }}\];
D. \[d\left( {M,\,\,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {x_0^2 + y_0^2} }}\].
Trong mặt phẳng tọa độ, cho hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0,
với các vectơ pháp tuyến \(\overrightarrow {{n_1}} = \left( {{a_1};\,\,b{ & _1}} \right)\) và \(\overrightarrow {{n_2}} = \left( {{a_2};\,\,b{ & _2}} \right)\) tương ứng. Khi đó góc φ giữa hai đường thẳng đó được xác định bởi công thức
A. \(\cos \varphi = \cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}\);
B. \(\cos \varphi = - \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = - \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = - \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}\);
C. \(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}\);
D. \(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + a_2^2} \cdot \sqrt {b_1^2 + b_2^2} }}\).
Khoảng cách từ điểm A(1; 1) đến đường thẳng d: 5x – 12y – 6 = 0 là
A. 13;
B. – 13;
C. – 1;
D. 1.
Góc giữa hai đường thẳng a: \(\sqrt 3 \)x – y + 7 = 0 và b: x – \(\sqrt 3 \)y – 2 = 0 là
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Phương trình nào sau đây là phương trình đường tròn?
A. 2x2 + y2 – 6x – 6y – 8 = 0;
B. x2 + 2y2 – 4x – 8y – 12 = 0;
C. x2 + y2 – 2x – 8y + 18 = 0;
D. 2x2 + 2y2 – 4x + 6y – 12 = 0.
Đường tròn (x + 1)2 + (y – 2)2 = 16 có bán kính bằng bao nhiêu?
A. 16;
B. 4;
C. 256;
D. 8.
Phương trình nào sau đây là phương trình của đường tròn tâm I(– 1; 2), có bán kính bằng 5?
A. (x – 1)2 + (y + 2)2 = 25;
B. (x + 1)2 + (y + 2)2 = 25;
C. (x + 1)2 + (y – 2)2 = 25;
D. (x – 1)2 + (y – 2)2 = 25.
Phương trình đường tròn có tâm I(3; 4) tiếp xúc với đường thẳng ∆: 3x + 4y – 10 = 0 là
A. (x – 3)2 + (y – 4)2 = 9;
B. (x + 3)2 + (y – 4)2 = 9;
C. (x – 3)2 + (y – 4)2 = 3;
D. (x + 3)2 + (y + 4)2 = 3.
Trong mặt phẳng tọa độ, cho đường tròn (C): (x – 2)2 + (y + 2)2 = 5. Tiếp tuyến tại điểm M(1; 0) thuộc đường tròn (C) có phương trình là
A. y = – 2;
B. x = 1;
C. x + 2y – 1 = 0;
D. x – 2y – 1 = 0.

