12 CÂU HỎI
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm như sau
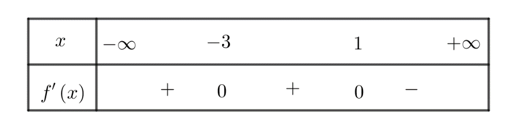
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. \(\left( {2; + \infty } \right)\).
B. \(\left( { - \infty ; - 2} \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( { - 2;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\), \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty \).
A. Đồ thị hàm số đã cho có hai tiệm cận ngang phân biệt.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng \(x = 2\).
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho không có tiệm cận ngang
Gọi giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{{\ln x}}{x}\) trên nửa khoảng \(\left[ {1;\,{e^2}} \right)\) lần lượt là \(m\) và \(M\). Giá trị của biểu thức \(\ln \left( {m + M} \right)\)bằng
A.\[1\].
B. \[ - 1\].
C. \[e\].
D. \({e^{ - 1}}\).
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
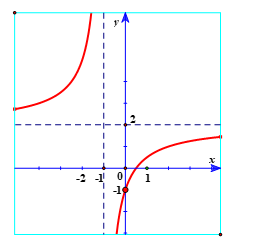
A. \(y = \frac{{2x + 1}}{{x + 1}}\).
B. \(y = \frac{{1 - 2x}}{{x - 1}}\).
C. \(y = \frac{{2x - 1}}{{x + 1}}\).
D. \(y = \frac{{2x + 1}}{{x - 1}}\).
Cho hình hộp \[ABCD.A'B'C'D'\]. Vectơ nào dưới đây cùng phương với vectơ \[\overrightarrow {AB} \]?
A. \[\overrightarrow {CD} \].
B. \[\overrightarrow {B'C'} \] .
C. \[\overrightarrow {AD} \].
D. \[\overrightarrow {AC'} \].
Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow a = 3\overrightarrow i + 4\overrightarrow j - \overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \)là
A.\(\overrightarrow a = \left( {3\;;\;4\;;\;1} \right)\).
B. \(\overrightarrow a = \left( {3\;;\;0\;;\;1} \right)\).
C. \(\overrightarrow a = \left( {3\;;\;4\;;\; - 1} \right)\).
D. \(\overrightarrow a = \left( {3\;;\;0\;;\;0} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\vec a\left( { - 1;0;3} \right)\)và\(\vec b\left( {1;2; - 1} \right)\). Tọa độ của vectơ \(\vec c = \vec a - \vec b\) là
A. \(\left( { - 1;0; - 2} \right)\).
B. \(\left( { - 2; - 2;4} \right)\).
C. \(\left( {2;2; - 4} \right)\).
D. \(\left( {0;2;2} \right)\).
Cho hình lăng trụ \(ABC.A'B'C'\), \(M\) là trung điểm của \(BB'\). Đặt \(\overrightarrow {CA} = \vec a\), \(\overrightarrow {CB} = \vec b\), \(\overrightarrow {AA'} = \vec c\). Khẳng định nào sau đây đúng?
A.\(\overrightarrow {AM} = \vec b + \vec c - \frac{1}{2}\vec a\).
B.\(\overrightarrow {AM} = \vec a - \vec c + \frac{1}{2}\vec b\).
C. \(\overrightarrow {AM} = \vec a + \vec c - \frac{1}{2}\vec b\).
D.\(\overrightarrow {AM} = \vec b - \vec a + \frac{1}{2}\vec c\).
Trong không gian \[Oxyz\], cho điểm \[I\left( { - 5;0;5} \right)\] là trung điểm của đoạn \[MN\], biết \[M\left( {1; - 4;7} \right)\]. Tìmtọa độ của điểm \[N\].
A.\[N\left( { - 10;4;3} \right)\].
B. \[N\left( { - 11; - 4;3} \right)\].
C.\[N\left( { - 2; - 2;6} \right)\].
D. \[N\left( { - 11;4;3} \right)\].
Trong không gian với hệ toạ độ \(Oxyz\), cho vectơ \(\overrightarrow a = \left( {0; - 1;1} \right),\,\,\overrightarrow b = \left( { - 1;0; - m} \right)\). Có bao nhiêu giá trị thực của \(m\) để góc giữa vectơ \(\overrightarrow a \) và vectơ \(\overrightarrow b \) bằng \(60^\circ \)?
A. \(1\).
B. \(0\).
C. \(2\).
D. \(3\).
Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào. Kết quả khảo sát được ghi lại ở bảng sau:
|
Mức giá (triệu đồng/\[{{\rm{m}}^{\rm{2}}}\]) |
[10;14) |
[14;18) |
[18;22) |
[22;26) |
[26;30) |
|
Số khách hàng |
54 |
78 |
120 |
45 |
12 |
Khoảng biến thiên \(R\) của mẫu số liệu ghép nhóm trên là.
A. \(R = 4\).
B. \(R = 20\).
C. \(R = 9\).
D. \(R = 108\).
Độ lệch chuẩn bằng
A. bình phương của phương sai.
B. một nửa của phương sai.
C. căn bậc hai số học của phương sai.
D. nghịch đảo của phương sai.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
