12 CÂU HỎI
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
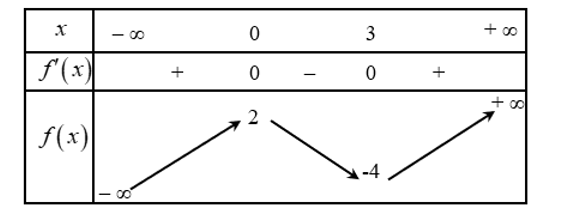
Đồ thị hàm số \(y = f\left( x \right)\) có điểm cực tiểu là
A. \[\left( {0\,;\,2} \right)\].
B. \(\left( {3\,;\, - 4} \right)\).
C. \({x_{CT}} = 3\).
D. \({y_{CT}} = - 4\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;2} \right]\) và có đồ thị như hình vẽ sau
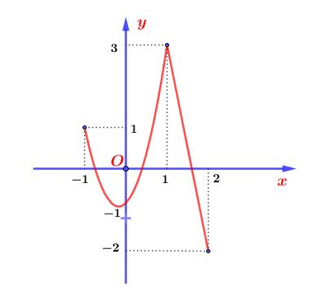
Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \[\left[ { - 1;2} \right]\] là
A. \[3\].
B. \[ - 1\].
C. \[1\].
D. \[2\]
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x - 2}}{{x + 1}}\) là
A. \(y = - 2\)
B. \(x = - 1\)
C. \(x = 2\)
D. \(y = 1\)
Đường cong ở hình bên dưới là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\)với \[a\],\[b\],\[c\],\[d\] là các số thực.
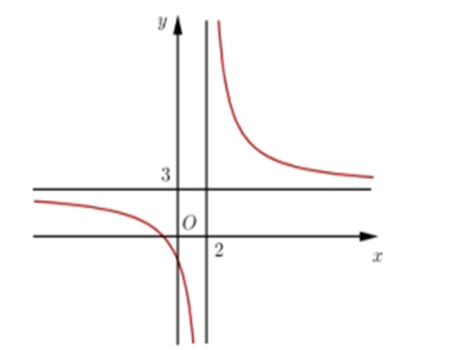
Mệnh đề nào dưới đây đúng?
A.\(y' > 0\),\(\forall x \ne 2\).
B. \(y' > 0\),\(\forall x \ne 3\).
C. \(y' < 0\),\(\forall x \ne 2\).
D. \(y' < 0\),\(\forall x \ne 3\).
Cho hàm số \(y = \frac{{{x^2} - 2x + 5}}{{x - 1}}\). Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng \(\left( { - 1;\,1} \right) \cup \left( {1\,;\,3} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { - 1;\,3} \right){\rm{\backslash }}\left\{ 1 \right\}\).
C. Hàm số nghịch biến trên mỗi khoảng \(\left( { - 1;\,1} \right)\)và \(\left( {1\,;\,3} \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
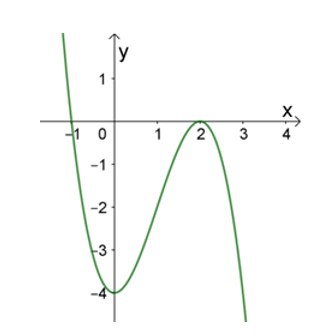
A. \(y = \frac{{x - 1}}{x}\).
B. \(y = {x^3} + 3{x^2} - 4\).
C. \(y = - {x^3} + 3x - 4\).
D. \(y = - {x^3} + 3{x^2} - 4\).
Trong không gian, cho hình hộp \(ABCD\,A'B'C'D'\). Vectơ đối của vectơ \[\overrightarrow {AA'} \]là
A.\[\overrightarrow {A'C'} \].
B. \[\overrightarrow {BA'} \].
C. \[\overrightarrow {BB'} \].
D. \[\overrightarrow {C'C} \].
Trong không gian \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\). Biết \(A\left( {1;0;1} \right)\), \(C'\left( {4;5; - 5} \right)\). Tìm tọa độ tâm \(I\) của hình hộp.
A. \(I\left( {5;5; - 2} \right)\).
B. \(I\left( { - \frac{5}{2};\frac{5}{2}; - 2} \right)\).
C. \(I\left( {\frac{5}{2};\frac{5}{2};2} \right)\).
D. \(I\left( {\frac{5}{2};\frac{5}{2}; - 2} \right)\).
Cho tứ diện \(S.ABC\) có đáy là tam giác đều cạnh \(a\), \(SB\) vuông góc với đáy và \(SB = \sqrt 3 a\). Góc giữa hai vectơ \(\left( {\overrightarrow {AB} ,\overrightarrow {AS} } \right)\) là
A. \[60^\circ \].
B. \[30^\circ \].
C. \[45^\circ \].
D. \[90^\circ \].
Trong không gian tọa độ \(Oxyz\), cho điểm \(A\left( {1;0; - 2} \right)\), \(B\left( {1; - 1;0} \right)\). Tìm toạ độ điểm \(C\)nằm trên trục \(Oz\) sao cho \(AB \bot BC\)?
A. \(\left( {0;0;1} \right)\).
B. \(\left( {0;0; - 1} \right)\).
C. \(\left( {0;0;\frac{1}{2}} \right)\).
D. \(\left( {0;0; - \frac{1}{2}} \right)\).
Thống kê chỉ số chất lượng không khí (AQI) tại một địa điểm vào các ngày trong tháng 6/2022 được cho trong bảng sau
|
Chỉ số AQI |
\(\left[ {0;50} \right)\) |
\(\left[ {50;100} \right)\) |
\(\left[ {100;150} \right)\) |
\(\left[ {150;200} \right)\) |
\(\left[ {200;250} \right)\) |
|
Số ngày |
5 |
11 |
7 |
4 |
3 |
Khoảng biến thiên \(R\) của mẫu số liệu ghép nhóm trên là.
A. \(R = 50\).
B. \(R = 250\).
C. \(R = 150\).
D. \(R = 8\).
Khẳng định nào sau đây sai?
A. Độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
B. Độ lệch chuẩn của mẫu số liệu ghép nhóm là căn bậc hai số học của phương sai.
C. Phương sai càng lớn thì mẫu số liệu càng phân tán.
D. Phương sai của mẫu số liệu ghép nhóm là căn bậc hai số học của độ lệch chuẩn.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải