12 CÂU HỎI
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ.
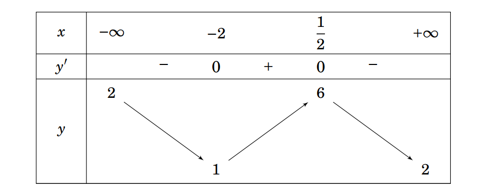
Chọn khẳng định đúng trong các khẳng định sau:
A. Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trong khoảng \(\left( { - \infty ; - 2} \right)\) là \(1\) .
B. Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trong khoảng \(\left( { - \infty ;\frac{1}{2}} \right)\) là \(6\).
C. Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trong khoảng \(\left( { - 2;\frac{1}{2}} \right)\) là \(1\).
D. Hàm số \(y = f\left( x \right)\) không có giá trị nhỏ nhất trên khoảng \(\left( { - 2; + \infty } \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên dưới. Đường thẳng nào sau đây là đường tiệm cận ngang của đồ thị hàm số đã cho?
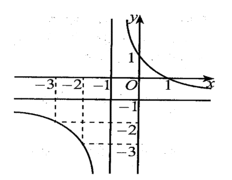
A. \(x = 1\).
B. \(x = - 1\).
C. \(y = 1\).
D. \(y = - 1\).
Bảng biến thiên sau là của hàm số nào dưới đây?
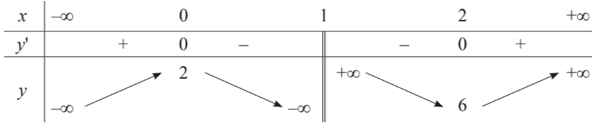
A. \(y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\).
B. \(y = \frac{{{x^2} + 2x - 2}}{{x + 1}}\).
C. \(y = \frac{{{x^2} + 2x + 2}}{{x - 1}}\).
D. \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).
Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(y = \frac{1}{3}{x^3} + {x^2} - mx - 1\) có đúng một điểm cực trị thuộc khoảng \(\left( {0;4} \right)\)?
A. \(23\).
B. \(8\).
C. \(9\).
D. Vô số.
Trong không gian với hệ tọa độ \(Oxyz\), cho các điểm \(A\left( {3; - 4;0} \right)\). Toạ độ \(\overrightarrow {OA} \) là
A. \(\left( {3;0;0} \right)\).
B. \(\left( {3; - 4;0} \right)\).
C. \(\left( {0; - 4;0} \right)\).
D. \(\left( {0;0;0} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hình chữ nhật \(OKMN\) ( hình vẽ bên).
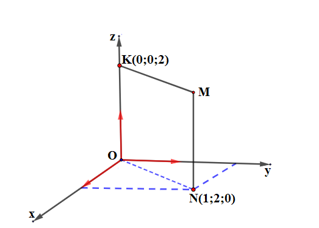
Tọa độ đỉnh \(M\)của hình chữ nhật là:
A. \(M\left( {1;\,2;\,2} \right)\).
B. \(M\left( { - 1; - \,2;\, - 2} \right)\).
C. \(M\left( {0;\,2;\,2} \right)\).
D. \(M\left( {1;2;\,0} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], với \[\overrightarrow i ,\overrightarrow j ,\overrightarrow k \] lần lượt là các vecto đơn vị trên các trục \[Ox,\,\,Oy,\,\,Oz.\] Tính tọa độ của vecto \[\overrightarrow i + \overrightarrow j - \overrightarrow k .\]
A. \[\left( { - 1; - 1;1} \right)\].
B. \[\left( { - 1;1;1} \right)\].
C. \[\left( {1;1; - 1} \right)\].
D. \[\left( {1; - 1;1} \right)\].
Cho điểm \(M\left( {3; - 2;0} \right);N\left( {2;4;1} \right)\). Tọa độ của\(\overrightarrow {MN} \) là:
A. \(\left( {1; - 6; - 1} \right)\).
B. \(\left( { - 1;6;1} \right)\).
C. \(\left( {1;0;6} \right)\).
D. \(\left( { - 1;6; - 1} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho \[\overrightarrow {OM} = \left( {1;5;2} \right)\], \[\overrightarrow {ON} = \left( {3;7; - 4} \right)\], \(K\left( { - 1;3;1} \right)\). Gọi \[P\] là điểm đối xứng với \[M\] qua \[N\]. Tìm tọa độ vectơ \[\overrightarrow {KP} \].
A. \(\overrightarrow {KP} = \left( {6;6; - 11} \right)\).
B. \[\overrightarrow {KP} = \left( {8;6; - 11} \right)\].
C. \[\overrightarrow {KP} = \left( {6;6; - 4} \right)\].
D. \[\overrightarrow {KP} = \left( {3;3; - 2} \right)\].
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\)có điểm \(A\) trùng với gốc tọa độ \(O\), điểm \(B\) nằm trên tia \(Ox\), điểm \(D\)nằm trên tia \(Oy\), điểm \(A'\)nằm trên tia \(Oz\).Biết \(AB = 2,\,AD = 4,\,AA' = 3\). Gọi tọa độ của \(C'\) là \(\left( {a;\,b;\,c} \right)\) khi đó biểu thức \(a + b - c\) có giá trị là.
A. \( - 4\).
B. \(9\).
C. \(3\).
D. \(6\).
Đại lượng nào đo độ phân tán của nửa giữa của mẫu số liệu, không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ trong mẫu số liệu?
A. Khoảng biến thiên.
B. Khoảng tứ phân vị.
C. Phương sai.
D. Độ lệch chuẩn.
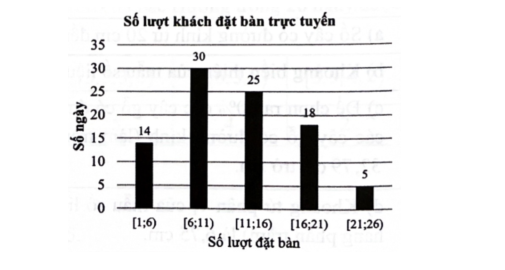
Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn;... Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên.
A. \(8\).
B. \(8,5\).
C. \(7,5\).
D. \(16\).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
