12 CÂU HỎI
Cho hàm số \[y = f\left( x \right)\] xác định, liên tục trên đoạn \[\left[ { - 2\,;\,2} \right]\] và có đồ thị là đường cong trong hình vẽ sau:
![Cho hàm số \[y = f\( x ] xác định, liên tục trên đoạn \[[ { - 2\,;\,2} \right]\] và có đồ thị là đường cong trong hình vẽ sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/12/blobid62-1734019675.png)
Tìm khẳng định đúng trong các khẳng định sau:
A. \[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = - 4\].
B. \[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = 1\].
C. \[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = 2\].
D. \[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = - 2\].
Tiệm cận đứng của đồ thị số hàm số \(y = \frac{{4{x^2} - x + 1}}{{3x + 2}}\) là đường thẳng
A. \(x = \frac{2}{3}\).
B. \(x = \frac{4}{3}\).
C. \(x = - \frac{2}{3}\).
D. \(x = - \frac{3}{2}\).
Gọi \(M,\)\(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{x + 1}}{{x - 1}}\) trên đoạn \(\left[ {3\,;\,5} \right].\) Khi đó \(M - m\) bằng
A. 2.
B. \(\frac{3}{8}\).
C. \(\frac{7}{2}\).
D. \(\frac{1}{2}\).
Đường cong trong hình bên là đồ thị của hàm số
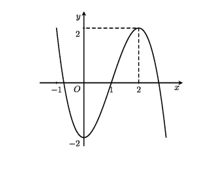
A.\(y = {x^3} - 3{x^2} - 2\).
B. \(y = - {x^3} + 3{x^2} + 2\).
C. \(y = - {x^3} + 3{x^2} - 2\).
D. \(y = {x^3} + 3{x^2} - 2\).
Cho tứ diện \(ABCD\) .Các véc tơ có điểm đầu là \(A\) và điểm cuối là các đỉnh còn lại của hình tứ diện là
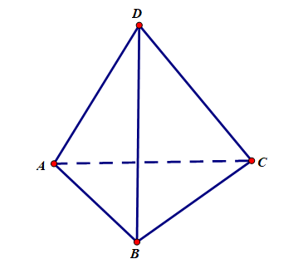
A. \[\overrightarrow {AB} ,\,\overrightarrow {CA} ,\,\overrightarrow {AD} .\]
B. \[\overrightarrow {BA} ,\,\overrightarrow {AC} ,\,\overrightarrow {AD} .\]
C. \[\overrightarrow {AB} ,\,\overrightarrow {AC} ,\,\overrightarrow {DA} .\]
D. \[\overrightarrow {AB} ,\,\overrightarrow {AC} ,\,\overrightarrow {AD} .\]
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;\,1;\, - 2} \right)\) và \(B\left( {2;\,2;\,1} \right)\). Vectơ \(\overrightarrow {AB} \) có tọa độ là
A. \(\left( { - 1;\, - 1;\, - 3} \right)\).
B. \(\left( {3;\,1;\,1} \right)\).
C. \(\left( {1;\,1;\,3} \right)\).
D. \(\left( {3;\,3;\, - 1} \right)\).
Trong không gian tọa độ \(Oxyz\), cho vectơ \(\vec u\left( {1; - 1;2} \right)\) . Khi đó vectơ \(\vec v = 3.\,\vec u\) có tọa độ là:
A. \(\vec v\left( {3; - 1;3} \right)\).
B. \(\vec v\left( {3; - 3;3} \right)\).
C. \(\vec v\left( {3; - 3;6} \right)\).
D. \(\vec v\left( { - 3;3; - 6} \right)\).
Cho hình chóp \(S.ABC\) có \(AB = 4,\widehat {BAC} = 60^\circ ,\overrightarrow {AB} \cdot \overrightarrow {AC} = 6\). Khi đó độ dài \(\overrightarrow {AC} \)là
A. \[3\].
B. \[6\].
C. \[4\].
D. \[12\].
Trong hệ tọa độ \(Oxyz,\)cho hai điểm \(A\left( {1;2; - 4} \right),{\rm{ }}B\left( { - 2;3;0} \right)\). Tìm tọa độ điểm \(I\) sao cho \(\overrightarrow {IA} + 2\overrightarrow {IB} = \overrightarrow 0 .\)
A. \(I\left( { - \frac{1}{2};\frac{5}{2}; - 2} \right)\).
B. \(I\left( {\frac{1}{2}; - \frac{5}{2};2} \right)\).
C. \(I\left( {1; - \frac{8}{3};\frac{4}{3}} \right)\).
D. \(I\left( { - 1;\frac{8}{3}; - \frac{4}{3}} \right)\).
Trong không gian \[Oxyz\],cho \(\overrightarrow a = \left( {3;2;1} \right)\), \(\overrightarrow b = \left( { - 2;0;1} \right)\). Độ dài của \(\overrightarrow a + \overrightarrow b \) là
A. \(3\).
B. \(1\).
C. \(2\).
D. \(\sqrt 2 \).
Cho mẫu số liệu ghép nhóm:
|
Nhóm |
\(\left[ {{a_1};{a_2}} \right)\) |
\( \ldots \) |
\(\left[ {{a_;};{a_{i + 1}}} \right)\) |
\( \ldots \) |
\(\left[ {{a_k};{a_{k + 1}}} \right)\) |
|
Tần số |
\({m_1}\) |
\( \ldots \) |
\({m_i}\) |
\( \ldots \) |
\({m_k}\) |
trong đó các tần số \({m_1} > 0,{m_k} > 0\) và \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu. Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
A.\(R = {a_{k + 1}} - {a_1}\).
B. \(R = {a_1} - {a_{k + 1}}\).
C. \(R = {a_{k + 1}} + {a_1}\).
D. \(R = {a_{k + 1}} - {a_k}\).
Ý nghĩa độ lệch chuẩn của mẫu số liệu ghép nhóm
A. dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó.
B. cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.
C. chia mẫu số liệu thành hai phần, mỗi phần chứa 50% giá trị.
D. chia mẫu số liệu thành bốn phần, mỗi phần chứa 25% giá trị.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
