50 CÂU HỎI
Thể tích khối lập phương tăng thêm bao nhiêu lần nếu độ dài cạnh của nó tăng gấp đôi?
A. 8.
B. 7.
C. 1.
D. 4.
Hàm số có điểm cực đại là
A.
B. x=0
C. M(0;5)
D. y=5
Trong không gian với hệ trục tọa độ Oxyz, nếu là véctơ chỉ phương của trục Oy thì
A. cùng hướng với .
B. cùng phương với .
C. cùng hướng với .
D. cùng phương với .
Trong các hàm số sau, hàm số nào nghịch biến trên ?
A.
B.
C.
D.
Cho a, b là các số thực dương, và . Mệnh đề nào sau đây là đúng?
A.
B.
C.
D.
Biết f(x) là hàm liên tục trên R và . Khi đó giá trị của là:
A. 0
B. 27
C. 3
D. 24
Cho hình trụ tròn xoay có thiết diện qua trục là hình vuông có diện tích . Thể tích khối trụ đã cho là:
A.
B.
C.
D.
Gọi là 2 nghiệm của phương trình . Khi đó giá trị là:
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng nào trong các mặt phẳng sau song song với trục Oz?
A.
B.
C.
D.
Cho biết hàm số có đạo hàm và có một nguyên hàm là . Tìm ?
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng . Phương trình chính tắc của d là:
A.
B.
C.
D.
Có bao nhiêu cách mắc nối tiếp 4 bóng đèn được chọn từ 6 bóng đèn khác nhau?
A. 15.
B. 360.
C. 24.
D. 17280.
Công thức nào sau đây là đúng với một cấp số cộng có số hạng đầu , công sai d và số tự nhiên .
A.
B.
C.
D.
Số phức liên hợp của số phức là
A.
B.
C.
D.
Cho hàm số có đồ thị như hình bên. Tính .
A. f(2)=15
B. f(2)=18
C. f(2)=16
D. f(2)=17
Cho hàm số f(x) liên tục trên đoạn và có đồ thị trên đoạn như hình vẽ bên. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn bằng:
![Cho hàm số f(x) liên tục trên đoạn [-1;5] và có đồ thị trên đoạn [-1;5] như hình vẽ bên. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [-1;5] bằng: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/dx-1652802687.png)
A. -1
B. 4
C. 1
D. 2
Tập hợp các số thực m để hàm số đạt cực tiểu tại là:
A.
B.
C.
D.
Tìm các giá trị của tham số thực x, y để số phức là số thực.
A. và
B.
C. hoặc
D. 1
Trong không gian với hệ tọa độ Oxyz, mặt cầu tâm tiếp xúc với Ox có bán kính R bằng:
A. R=6
B. R=5
C. R=4
D. R=3
Cho với . Mệnh đề nào sau đây là đúng?
A.
B.
C.
D.
Kí hiệu là nghiệm phức của phương trình . Tính giá trị biểu thức .
A. P=1
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, lập phương trình của các mặt phẳng song song với mặt phẳng và cách một khoảng bằng .
A. và .
B. .
C. và .
D. và .
Tập nghiệm của bất phương trình là:
A.
B.
C.
D.
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số và các đường được xác định bởi công thức:
A.
B.
C.
D.
Cho hình nón tròn xoay có đường cao h=20cm. Gọi là góc ở đỉnh của hình nón với . Độ dài đường sinh của hình nón là:
A. 25cm.
B. 35cm.
C. 15cm.
D. 45cm.
Có bao nhiêu giá trị m để đồ thị hàm số có đúng hai đường tiệm cận?
A. 1
B. 2
C. 3
D. 4
Cho khối lăng trụ đứng ABC.A’B’C’ có , đáy ABC là tam giác vuông cân tại B và . Tính thể tích V của khối lăng trụ đã cho.
A.
B.
C.
D.
Đạo hàm của hàm số là:
A.
B.
C.
D.
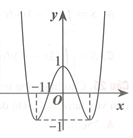
Cho hàm số xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ:
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình có 3 nghiệm thực phân biệt.
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB=a, BC=2a . Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD), cạnh . Tính góc tạo bởi đường thẳng SC và mặt phẳng (ABD).
A.
B.
C.
D.
Biết rằng phương trình có hai nghiệm phân biệt . Tính .
A.
B.
C.
D.
Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1, chiều cao bằng 2. Người ta khoét từ hai đầu khối gỗ hai nửa khối cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu. Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là:
A.
B.
C.
D.
Họ nguyên hàm của hàm số là:
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng (ABCD) góc . Tính khoảng cách d từ B đến mặt phẳng (SDC) theo a.
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng và đường thẳng . Hình chiếu của d trên có phương trình là:
A.
B.
C.
D.
Tìm tất cả các giá trị của m để hàm số nghịch biến trên đoạn có độ dài bằng 2?
A.
B.
C.
D.
Môđun của số phức z thỏa mãn và bằng:
A.
B.
C. và .
D. .
Cho hàm số f(x) có đạo hàm trên R thỏa mãn . Đặt , m là tham số nguyên và m<27. Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số g(x) đạt cực tiểu tại x=0. Tính tổng bình phương các phần tử của S.
A. 100.
B. 50.
C. 108.
D. 58.
Một tỉnh A đưa ra nghị quyết về giảm biên chế cán bộ công chức, viên chức hưởng lương từ ngân sách nhà nước trong giai đoạn 2015-2021 (6 năm) là 10,6% so với số lượng hiện có năm 2015 theo phương thức “ra 2 vào 1” (tức là khi giảm đối tượng hưởng lương từ ngân sách nhà nước 2 người thì được tuyển mới 1 người). Giả sử tỉ lệ giảm và tuyển dụng mới hàng năm so với năm trước đó là như nhau. Tính tỉ lệ tuyển dụng mới hàng năm (làm tròn đến 0,01%).
A. 1,13%.
B. 1,72%.
C. 2,02%.
D. 1,85%.
Trong trò chơi “Chiếc nón kì diệu” chiếc kim của bánh xe có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau.
A.
B.
C.
D.
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số trên đoạn đạt giá trị nhỏ nhất?
A. 2.
B. 3.
C. 0.
D. 1.
Một bác thợ xây bơm nước vào bể chứa nước. Gọi V(t) là thể tích nước bơm được sau t giây. Biết rằng và ban đầu bể không có nước, sau 5 giây thể tích nước trong bể là , sau 10 giây thì thể tích nước trong bể là . Thể tích nước bơm được sau 20 giây bằng:
A.
B.
C.
D.
Trong không gian hệ tọa độ Oxyz, cho mặt cầu và các điểm . Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng . Tính
A. 3.
B. -3
C. 0.
D. -2
Cho hàm số f(x) có đồ thị như hình vẽ:
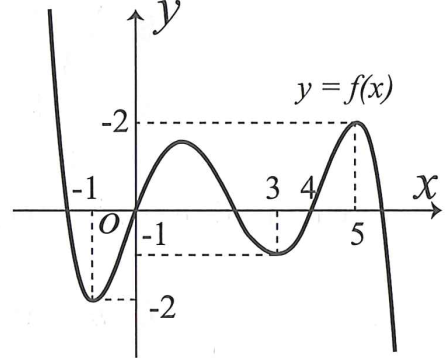
Có bao nhiêu giá trị nguyên của để có nghiệm?
A. 8.
B. 6.
C. 9.
D. 7.
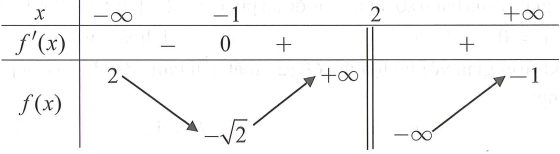
Cho hàm số y=f(x) . Hàm số y=f'(x) có bảng biến thiên như sau:

Bất phương trình nghiệm đúng với mọi khi chỉ khi
A.
B.
C.
D.
Cho khối lăng trụ tam giác ABC.A’B’C’. Gọi I, J, K lần lượt là trung điểm của các cạnh AB, AA’ và B’C’. Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó.
A.
B. 1.
C.
D.
Cho thỏa mãn . Giá trị lớn nhất của bằng:
A.
B.
C.
D.
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [0;1] và thỏa mãn f(0)=0. Biết và . Tích phân bằng.
A.
B.
C.
D.
Cho hàm số y=f(x) và . Biết hàm số có bảng biến thiên như hình vẽ và .
![Có bao nhiêu giá trị nguyên của m thuộc [-2020;2020] để hàm số g(x) =e^(-x^2+4mx-5).f(x)đồng biến trên . (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/zzzzzz-1652952307.png)
Có bao nhiêu giá trị nguyên của để hàm số đồng biến trên .
A. 4040.
B. 4041.
C. 2019.
D. 2020.
Cho cấp số cộng , cấp số nhân thỏa mãn và hàm số sao cho và . Tìm số nguyên dương n nhỏ nhất sao cho .
A. 17.
B. 14.
C. 15.
D. 16.


