50 câu hỏi
Gọi \(M,N\) là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} - 3x + 1\) trên \(\left[ {0;2} \right].\) Khi đó \(M + N\) bằng
3.
4.
6.
2.
Nghiệm của phương trình \({\log _2}\left( {3x - 2} \right) = 2\) là
\(x = \frac{2}{3}.\)
\(x = 2.\)
\(x = 1.\)
\(x = \frac{4}{3}.\)
Cho khối nón có chu vi đáy \(8\pi \) và chiều cao \(h = 3.\) Thể tích khối nón đã cho bằng?
\(12\pi .\)
\(4\pi .\)
\(16\pi .\)
\(24\pi .\)
Với \(a >0,a \ne 1,{\log _{{a^3}}}a\) bằng
3.
\( - 3.\)
\(\frac{1}{3}.\)
\(\frac{{ - 1}}{3}.\)
Số phức liên hợp của số phức \(4 - 3i\) là
\(3 + 4i.\)
\( - 4 - 3i.\)
\(3 - 4i.\)
\(4 + 3i.\)
Họ các nguyên hàm của hàm số \(f\left( x \right) = {x^2} + 2x + 3\) là
\(\frac{{{x^3}}}{3} + {x^2} + 3x + C.\)
\(2x + 2 + C.\)
\({x^3} + {x^2} + C.\)
\({x^3} + 2{x^2} + 3x + C.\)
Đồ thị hàm số \(y = \frac{{x - 3}}{{6 - 3x}}\) có bao nhiêu tiệm cận đứng và tiệm cận ngang?
3.
1.
2.
0.
Cho các số thực dương \(a,b,x,y\) thỏa mãn \(a >1,b >1\) và \({a^{x - 1}} = {b^y} = \sqrt[3]{{ab}}.\) Giá trị nhỏ nhất của biểu thức \(P = 3x + 4y\) thuộc tập hợp nào dưới đây?
\(\left( {7;9} \right].\)
\(\left( {11;13} \right).\)
\(\left( {1;2} \right).\)
\(\left[ {5;7} \right).\)
Cho số phức \(z\) thỏa \(\left( {2 + i} \right)z - 4\left( {\overline z - i} \right) = - 8 + 19i.\) Mô đun của \(z\) bằng
5
18.
\(\sqrt 5 .\)
\(\sqrt {13} .\)
Tìm tất cả giá trị thực của tham số \(m\) sao cho khoảng \(\left( {2;3} \right)\) thuộc tập nghiệm của bất phương trình \({\log _5}\left( {{x^2} + 1} \right) >{\log _5}\left( {{x^2} + 4x + m} \right) - 1.\)
\(m \in \left[ { - 12;13} \right].\)
\(m \in \left[ { - 13;12} \right].\)
\(m \in \left[ { - 13; - 12} \right].\)
\(m \in \left[ {12;13} \right].\)
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left( {0; + \infty } \right).\) Biết \(\frac{1}{{{x^2}}}\) là một nguyên hàm của hàm số \(y = f'\left( x \right)\ln x\) và \(f\left( 2 \right) = \frac{1}{{\ln 2}}.\) Khi đó, \(\int\limits_1^2 {\frac{{f\left( x \right)}}{x}dx} \) bằng
\( - \frac{7}{4}.\)
\(\frac{1}{2}.\)
\( - \frac{1}{2}.\)
\(\frac{7}{4}.\)
Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( \alpha \right):x + 2y - 1 = 0.\) Vectơ nào sau đây là một vectơ pháp tuyến của \(\left( \alpha \right)?\)
\(\left( {1;2; - 1} \right).\)
\(\left( {1;2;0} \right).\)
\(\left( {1; - 2;0} \right).\)
\(\left( { - 1;2;0} \right).\)
Cho số phức \(z = a + bi\) và \[{\rm{w}} = \frac{1}{2}\left( {z + \overline z } \right).\] Mệnh đề nào sau đây ĐÚNG?
\[{\rm{w}} = 2.\]
\[{\rm{w}}\]là một số thực.
\[w = i.\]
\[{\rm{w}}\] là số thuần ảo.
Cho một khối chóp có diện tích đáy \(B = 6{a^2},\) chiều cao \(h = 3a.\) Thể tích khối chóp đã cho bằng
\(6{a^3}.\)
\(18{a^3}.\)
\(9{a^3}.\)
\(54{a^3}.\)
Cho tích phân: \(I = \int\limits_1^e {\frac{{\sqrt {1 - \ln x} }}{x}dx} .\) Đặt \(u = \sqrt {1 - \ln x} .\) Khi đó \(I\) bằng
\(I = 2\int\limits_0^1 {{u^2}du} .\)
\(I = - 2\int\limits_0^1 {{u^2}du} .\)
\(I = \int\limits_1^0 {\frac{{{u^2}}}{2}du} .\)
\(I = - \int\limits_1^0 {{u^2}du} .\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và \(f'\left( x \right) = \left( {x - 2} \right){\left( {x + 3} \right)^4}{\left( {1 - 2x} \right)^3}.\) Số điểm cực trị của hàm số đã cho là
2.
3.
1.
0.
Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 5x + 4\) và trục \(Ox.\) Thể tích của khối tròn xoay sinh ra khi quay hình \(\left( H \right)\) quanh trục \(Ox\) bằng:
\(\frac{9}{2}.\)
\(\frac{{81}}{{10}}.\)
\(\frac{{81\pi }}{{10}}.\)
\(\frac{{9\pi }}{2}.\)
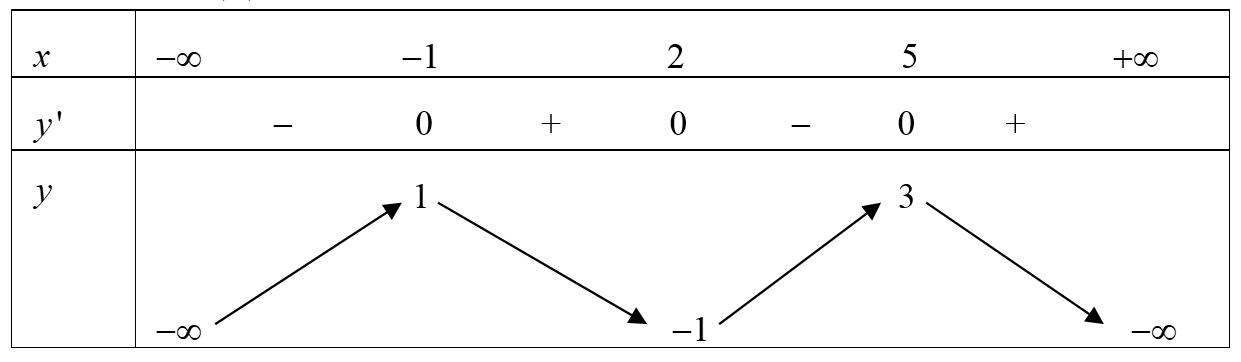
Cho hàm số \(f\left( x \right).\) Bảng biến thiên của hàm số \(f'\left( x \right)\) như sau:
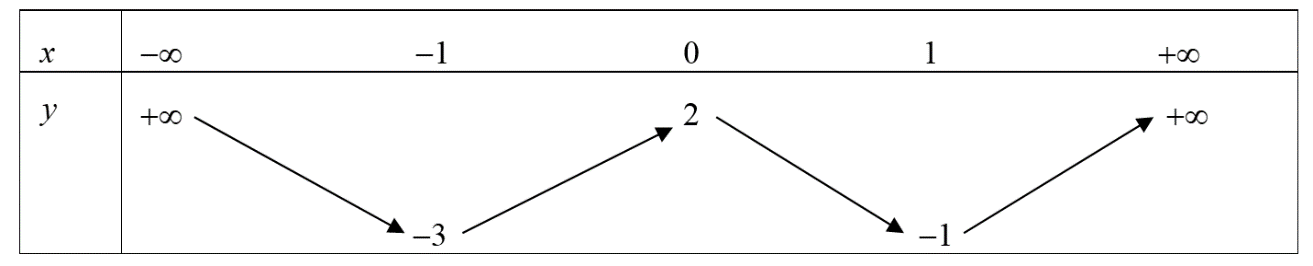
Số điểm cực trị của hàm số \(y = f\left( {{x^2} - 2x} \right)\) là:
7.
9.
3.
5.
Số giao điểm của đồ thị hàm số \(y = - {x^4} + 4{x^2} + 1\) và đồ thị hàm số \(y = {x^2} - 1\) là
4.
3.
2.
1.
Hàm số \(y = \frac{{x - {m^2}}}{{x - 4}}\) đồng biến trên các khoảng \(\left( { - \infty ;4} \right)\) và \(\left( {4; + \infty } \right)\) khi
\( - 2 \le m \le 2.\)
\(\left[ \begin{array}{l}m < - 2\\m >2\end{array} \right..\)
\(\left[ \begin{array}{l}m \le - 2\\m \ge 2\end{array} \right..\)
\( - 2 < m < 2.\)
Cho hình nón \(\left( N \right)\) có đỉnh \(S,\) bán kính đáy \(r = 1\) và độ dài đường sinh \(l = 2\sqrt 2 .\) Mặt cầu đi qua \(S\) và đường tròn đáy của \(\left( N \right)\) có bán kính bằng
\(\frac{{4\sqrt 7 }}{7}.\)
\(\frac{{8\sqrt 7 }}{7}.\)
\(\sqrt 7 .\)
\(\frac{4}{3}.\)
Tỉ lệ tăng dân số hàng năm của một quốc gia \(X\) là 0,2%. Năm 1998 dân số của quốc gia \(X\) là 125500000 người. Hỏi sau bao nhiêu năm thì dân số của quốc gia \(X\) là 140000000 người?
54 năm.
6 năm.
55 năm.
5 năm.
Cho hàm số \(y = \frac{{x + 1}}{{1 - x}}.\) Phát biểu nào sau đây đúng?
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\) và \(\left( { - 1; + \infty } \right).\)
Hàm số đồng biến trên \(\left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right).\)
Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right).\)
Hàm số đồng biến trên khoảng \(\left( { - 1; + \infty } \right).\)
Cho hình nón có bán kính đáy \(r = 2\) và độ dài đường sinh \(l = 4.\) Diện tích xung quanh của hình nón đã cho bằng
\(32\pi .\)
\(8\pi .\)
\(16\pi .\)
\(48\pi .\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình dưới. Số nghiệm thực của phương trình \(f\left( x \right) = - 1\) là
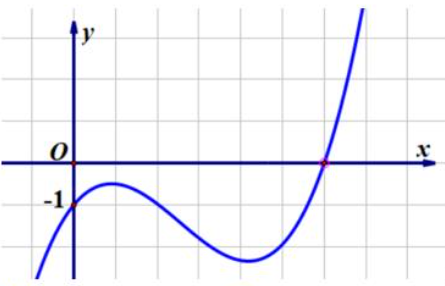
3.
2.
4.
1.
Xét các số phức \(z\) thỏa mãn \(\left| {i\overline z + 3 - 2i} \right| = 4.\) Trên mặt phẳng tọa độ \(Oxy,\) tập hợp điểm biểu diễn số phức \(w = 2i\overline z + 5 - 6i\) là một đường tròn có tâm \(I\left( {a;b} \right)\), bán kính \(R.\) Tính \(T = a + b + R\)
21.
17.
5.
\( - 1.\)
Hàm số \(y = {x^3} - 3{x^2} - 9x - 7\) đạt cực đại tại
\(x = 3.\)
\(\left\{ \begin{array}{l}x = - 1\\x = 3\end{array} \right..\)
\(\left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right..\)
\(x = - 1.\)
Cho đồ thị hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) như hình vẽ bên. Khẳng định nào sau đây là đúng
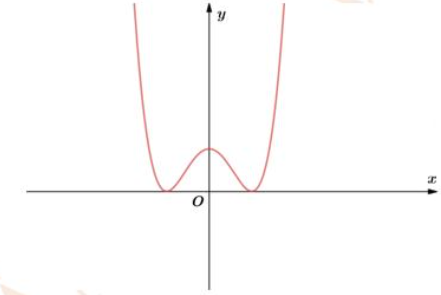
\(a >0;b < 0;c >0;{b^2} - 4ac = 0.\)
\(a >0;b >0;c >0;{b^2} - 4ac = 0.\)
\(a >0;b < 0;c >0;{b^2} - 4ac >0.\)
\(a >0;b < 0;c >0;{b^2} - 4ac < 0.\)
Trong không gian \[Oxyz,\] mặt phẳng qua \(A\left( {3;4;1} \right)\) và song song với mặt phẳng \(\left( {Oxy} \right)\) có phương trình là
\(x - 3 = 0.\)
\(z - 1 = 0.\)
\(y - 4 = 0.\)
\(3x + 4y + z = 0.\)
Nghiệm của phương trình \({9^{2x + 3}} = 81\) là
\(x = - \frac{3}{2}.\)
\(x = \frac{1}{2}.\)
\(x = - \frac{1}{2}.\)
\(x = \frac{3}{2}.\)
Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\left[ {1;2} \right],f\left( 1 \right) = 1\) và \(f\left( 2 \right) = 2.\) Khi đó, \(I = \int\limits_1^2 {f'\left( x \right)dx} \) bằng
\(I = 1.\)
\(I = - 1.\)
\(I = \frac{7}{2}.\)
\(I = 3.\)
Tập nghiệm của bất phương trình \({\left( {\frac{3}{4}} \right)^{2x - 4}} >{\left( {\frac{3}{4}} \right)^{x - 1}}\) là
\(\left( { - 1;2} \right).\)
\(\left( { - \infty ;5} \right).\)
\(\left[ {5; + \infty } \right).\)
\(\left( { - \infty ; - 1} \right).\)
Số cạnh của hình bát diện đều là
8.
12.
10.
20.
Thể tích của khối cầu có bán kính \(r = 3\) là
\(64\pi .\)
\(48\pi .\)
\(8\pi .\)
\(36\pi .\)
Trong không gian \(Oxyz,\) hình chiếu vuông góc của điểm \(A\left( {1;3;5} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) là điểm nào sau đây?
\(\left( {1;3;0} \right).\)
\(\left( {1;0;5} \right).\)
\(\left( {0;3;5} \right).\)
\(\left( {1;0;0} \right).\)
Biết \(\int\limits_0^2 {f\left( x \right)dx} = 2020,\) khi đó \(I = \int\limits_0^4 {\left[ {f\left( {\frac{x}{2}} \right)} \right]dx} \) bằng
2020.
1010.
\( - 2020.\)
4040.
Cho số phức \(z = 3 + 4i.\) Tìm phần thực \(a\) và phần ảo \(b\) của số phức \(z.\)
\(a = 3,b = 4.\)
\(a = 4,b = 3.\)
\(a = 4,b = - 3.\)
\(a = 3,b = - 4.\)
Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right):{\left( {x - 2} \right)^2} + {y^2} + {\left( {z + 1} \right)^2} = 4.\) Tâm của \(\left( S \right)\) có tọa độ là
\(\left( { - 2;0;1} \right).\)
\(\left( { - 2;0; - 1} \right).\)
\(\left( {2;0;1} \right).\)
\(\left( {2;0; - 1} \right).\)
Cho số phức \(z = \frac{{1 + 2i}}{{1 - i}}.\) Trong mặt phẳng tọa độ, điểm biểu diễn số phức \(z\) là điểm nào dưới đây?
\(\left( {\frac{1}{2}; - \frac{3}{2}} \right).\)
\(\left( { - \frac{1}{2}; - \frac{3}{2}} \right).\)
\(\left( {\frac{1}{2};\frac{3}{2}} \right).\)
\(\left( { - \frac{1}{2};\frac{3}{2}} \right).\)
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng \(2a.\) Thể tích khối trụ bằng
\(\pi {a^3}.\)
\(\frac{{2\pi {a^3}}}{3}.\)
\(\frac{{\pi {a^3}}}{3}.\)
\(2\pi {a^3}.\)
Đồ thị hình bên là của hàm số nào?
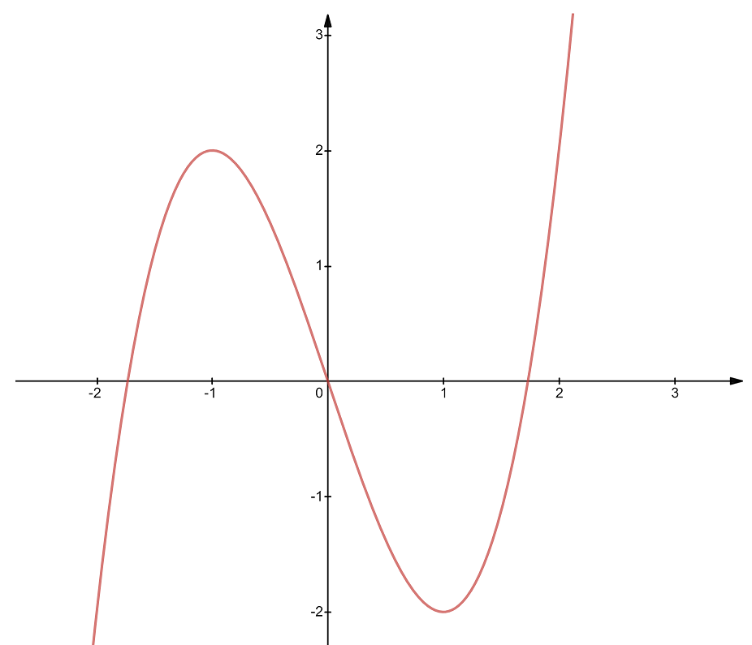
\(y = - {x^3} + 2x.\)
\(y = {x^3} - 3x.\)
\(y = {x^3} + 3x.\)
\(y = - {x^3} - 2x.\)
Trong không gian \(Oxyz,\) cho điểm \(A\left( {1;2;5} \right)\) và mặt phẳng \(\left( P \right):x - 2y + z - 1 = 0.\) Phương trình đường thẳng qua \(A\) vuông góc với \(\left( P \right)\) là:
\(\left\{ \begin{array}{l}x = 3 - t\\y = - 2 + 2t\\x = 7 - t\end{array} \right..\)
\(\left\{ \begin{array}{l}x = 1 - t\\y = 2 - 2t\\z = 5 - t\end{array} \right..\)
\(\left\{ \begin{array}{l}x = 2 - t\\y = - 2 + 2t\\z = 7 - t\end{array} \right..\)
\(\left\{ \begin{array}{l}x = 1 + t\\y = 2 - 2t\\z = 5 - t\end{array} \right..\)
Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc và \(OB = OC = a\sqrt 6 ,OA = a.\) Thể tích khối tứ diện đã cho bằng
\(3{a^3}.\)
\(2{a^3}.\)
\(6{a^3}.\)
\({a^3}.\)
Cho khối lăng trụ có diện tích đáy \(B = 8\) và chiều cao \(h = 6.\) Thể tích của khối lăng trụ đã cho bằng
48.
16.
24.
14.
Tập xác định của hàm số \(y = {\log _2}\frac{{x + 3}}{{2 - x}}\) là
\(\left( { - 3;2} \right).\)
\(\left( { - \infty ; - 3} \right) \cup \left( {2; + \infty } \right).\)
\(\mathbb{R}\backslash \left\{ { - 3;2} \right\}.\)
\(\left[ { - 3;2} \right].\)
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y + 2}}{3} = z + 1,\) điểm nào dưới đây thuộc đường thẳng \(d?\)
\(\left( {2;3;0} \right).\)
\(\left( {2;3;1} \right).\)
\(\left( {1; - 2; - 1} \right).\)
\(\left( { - 1;2;1} \right).\)
Trong không gian \(Oxyz,\) cho điểm \(A\left( {4; - 1;3} \right)\) và đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{1}.\) Tọa độ điểm \(M\) là điểm đối xứng với điểm \(A\) qua \(d\) là
\(M\left( {0; - 1;2} \right).\)
\(M\left( {2; - 5;3} \right).\)
\(M\left( { - 1;0;2} \right).\)
\(M\left( {2; - 3;5} \right).\)
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
Số nghiệm của phương trình \(f\left( {{2^{3{x^4} - 4{x^2} + 2}}} \right) + 1 = 0\) là
2.
3.
1.
5.
Cho các số thực \(a,b,c\) thỏa mãn \({a^{{{\log }_3}7}} = 27,{b^{{{\log }_7}11}} = 49,{c^{{{\log }_{11}}25}} = \sqrt {11} .\) Giá trị của biểu thức \(A = {a^{{{\left( {{{\log }_3}7} \right)}^2}}} + {b^{{{\left( {{{\log }_7}11} \right)}^2}}} + {c^{{{\left( {{{\log }_{11}}25} \right)}_2}}}\) là
129.
519.
469.
729.
Cho khối tứ diện \(ABCD\) có thể tích \(V.\) Gọi \({G_1},{G_2},{G_3},{G_4}\) lần lượt là trọng tâm của bốn mặt của hình tứ diện. Thể tích khối tứ diện \({G_1}{G_2}{G_3}{G_4}\) bằng
\(\frac{V}{{32}}.\)
\(\frac{V}{9}.\)
\(\frac{V}{{27}}.\)
\(\frac{V}{{12}}.\)
