50 câu hỏi
Kí hiệu , là nghiệm của phương trình . Giá trị của .
10.
6.
.
4.
Trong không gian Oxyz, cho điểm và mặt phẳng (P): . Mặt cầu tâm I và tiếp xúc với có phương trình là
.
.
.
.
Trong không gian Oxyz, đường thẳng d: có một vectơ chỉ phương là
.
.
.
.
Với a, b là số thực dương tùy ý, bằng
.
.
.
.
Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng (d) :
.
.
.
.
Cho hàm số y=f(x) xác định trên R\{1} , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
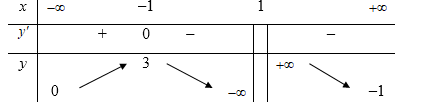
Số giá trị nguyên của tham số m để phương trình có 3 nghiệm thực phân biệt là
0.
3.
2.
1.
Họ nguyên hàm của hàm số
.
.
.
.
Cho hình phẳng giới hạn bởi đồ thị hàm số và trục hoành. Thể tích vật thể tròn xoay khi quay quanh trục hoành bằng
.
.
.
.
Đặt , khi đó bằng
.
.
.
.
Cho và , khi đó bằng
8.
15.
–8.
–15.
Có bao nhiêu cách xếp chỗ ngồi cho 4 bạn học sinh vào 4 chiếc ghế kê thành một hàng ngang?
24.
8.
4.
12.
Hàm số nào dưới đây có bảng biến thiên như hình vẽ?
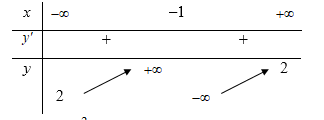
.
.
.
.
Trong không gian Oxyz, tích vô hướng của hai vectơ và bằng
–10.
–15.
15.
–7.
Cho hàm số có đạo hàm , . Giá trị lớn nhất của hàm số đã cho trên đoạn bằng
.
.
.
.
Tập nghiệm của phương trình là
.
.
.
.
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh , và SA vuông góc với mặt phẳng đáy. Thể tích khối chóp đã cho bằng
.
.
.
.
Tập nghiệm của bất phương trình là
.
.
.
Cho cấp số nhân có và công bội . Giá trị của bằng
.
.
.
.
Giả sử a, b là hai số thực thỏa mãn 2a(b-3)i=4-5i , với i là đơn vị ảo. Giá trị của a, b bằng
a=-2; b=2.
a=8, b=8
a=1, b=8
a=2, b=2
Cho hàm số y=f(x) có đồ thị như hình vẽ
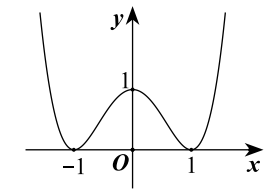
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
.
.
.
.
Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng 2a. Thể tích khối nón đã cho bằng
.
.
.
.
Cho hàm số y=f(x) đồ thị như hình vẽ
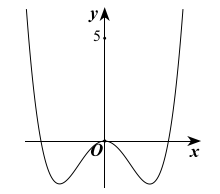
Số nghiệm thực của phương trình là
0.
3.
1.
2.
Trong không gian Oxyz, cho điểm A(1;2;3) và mặt phẳng (P) : 3x-4y+7z+2=0 . Đường thẳng đi qua A và vuông góc với mặt phẳng (P) có phương trình là
.
.
.
.
Cho hình trụ có bán kính đáy bằng 3 và chiều cao bằng 4. Diện tích xung quanh của hình trụ đã cho bằng
.
.
.
.
Tọa độ điểm biểu diễn số phức liên hợp của số phức z=2+5i là
.
.
.
Trong không gian hệ tọa độ Oxyz, cho mặt cầu (S): và mặt phẳng (P) : . Hai mặt cầu có bán kính là và chứa đường tròn giao tuyến của và đồng thời tiếp xúc với mặt phẳng (Q): . Tổng bằng
.
5.
.
.
Cho hình lập phương có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh và BC sao cho và . Mặt phẳng chia khối lập phương đã cho thành hai khối đa diện. Gọi là thể tích khối đa diện chứa đỉnh A , là thể tích khối đa diện còn lại. Tỉ số bằng
.
.
.
.
Cho hình chóp S.ABC có , , và SA vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là hình chiếu vuông góc của A trên SB và SC. Thể tích khối cầu ngoại tiếp hình chóp A.BCMN bằng.
.
.
.
.
Cho hàm số y=f(x) có bảng biến thiên như sau
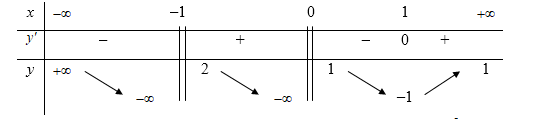
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
6.
5.
4.
3.
Trong không gian Oxyz, cho hai mặt phẳng (P):x+3z+2=0 , (Q) : x+3z-4=0 . Mặt phẳng song song và cách đều (P) , (Q) có phương trình là
.
.
.
Trong không gian Oxyz, cho mặt phẳng : . Gọi A, B, C lần lượt là giao điểm của với 3 trục tọa độ, đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với có phương trình là
.
.
.
.
Một khuôn viên dạng nửa hình tròn, trên đó người ta thiết kế phần trồng hoa hồng có dạng một hình parabol có đỉnh trùng với tâm hình tròn và có trục đối xứng vuông góc với đường kính của nửa đường tròn, hai đầu mút của parabol nằm trên nửa đường tròn cách nhau một khoảng 4 mét (phần tô đậm). Phần còn lại của khuôn viên (phần không tô màu) dùng để trồng hoa cúc. Biết các kích thước cho như hình vẽ. Chi phí trồng hoa hồng và hoa cúc lần lượt là 120.000 đồng / và 80.000 đồng / .
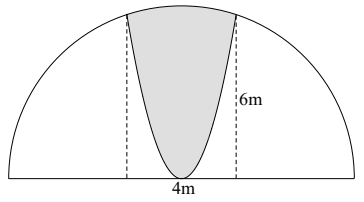
Chi phí trồng hoa khuôn viên đó gần nhất với số tiền nào dưới đây (làm tròn đến nghìn đồng)?
6.847.000 đồng.
6.865.000 đồng.
5.710.000 đồng.
5.701.000 đồng.
Đầu mỗi tháng, chị B gửi vào ngân hàng 3 triệu đồng theo hình thức lãi kép với lãi suất 0,6% một tháng và lãi suất không thay đổi suốt quá trình gửi tiền. Hỏi sau bao nhiêu tháng chị B có một số tiền cả gốc và lãi nhiều hơn 150 triệu đồng?
44 tháng.
43 tháng.
46 tháng.
47 tháng.
Xác định các hệ số a, b, c để đồ thị hàm số có
đồ thị hàm số như hình vẽ bên:
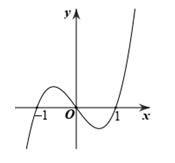
a=2, b=2, c=-1.
a=2, b=-1, c=1
a=2, b=1, c=1
a=2, b=1, c=-1
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, cạnh bằng , , SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và (ABCD) bằng 45°. Gọi G là trọng tâm tam giác SCD. Khoảng cách giữa hai đường thẳng OG và AD bằng
.
.
.
.
Cho với a, b, c là các số hữu tỉ. Giá trị của bằng
.
.
1.
0.
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ
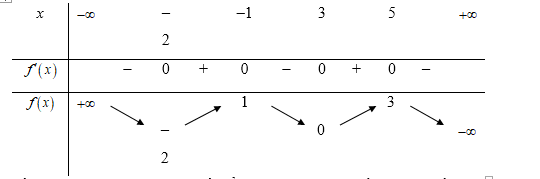
Xét hàm số Số điểm cực trị của hàm số y=g(x) bằng
9.
1.
5.
2.
Cho n là số nguyên dương thỏa mãn . Hệ số của số hạng chứa M trong khai triển biểu thức bằng:
29568.
–1774080.
–14784.
14784.
Cho hàm số thỏa mãn và có bảng biến thiên như sau
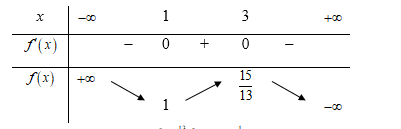
Giá trị lớn nhất của m để phương trình có nghiệm trên đoạn là
.
.
.
.
Cho số phức z thỏa mãn là một số thực. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường thẳng. Khoảng cách từ gốc tọa độ đến đường thẳng đó bằng:
.
0.
.
.
Để giá trị lớn nhất của hàm số đạt giá trị nhỏ nhất thì I bằng
.
.
Giả sử z là các số phức z thỏa mãn |iz-2+i|=3 . Giá trị lớn nhất của biểu thức 2|z-4-i|+|z+5+8i| bằng
.
.
.
.
Tập hợp tất cả các giá trị của tham số m để hàm số có hai điểm cực trị nằm về hai phía trục hoành khoảng . Giá trị của bằng
.
.
1.
Tổng tất cả các nghiệm của phương trình bằng:
.
.
.
.
Cho khối tứ diện ABCD có thể tích , góc và . Hỏi độ dài cạnh CD?
.
.
.
2.
Cho khối lăng trụ đứng có đáy ABC là tam giác vuông cân tại B, , . Góc giữa đường thẳng và mặt phẳng bằng
30°.
90°.
45°.
60°.
Cho hàm số y=f(x) có bảng biến thiên như sau
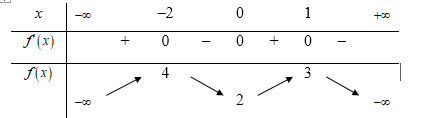 Số giá trị nguyên dương của tham số m để bất phương trình có nghiệm trên khoảng
Số giá trị nguyên dương của tham số m để bất phương trình có nghiệm trên khoảng
68.
18.
229.
230.
Cho hàm số có đạo hàm liên tục trên khoảng biết , , và . Tính giá trị của .
.
.
.
.
Cho hàm số , hàm số Scó đồ thị như hình vẽ. Hàm số nghịch biến trên khoảng nào dưới đây?
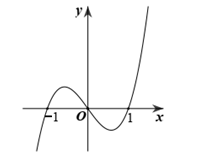
.
.
.
.
Cho hàm số y=f(x) liên tục và xác định trên R và có đồ thị hàm số y=f'(x) như hình vẽ
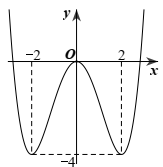
Bất phương trình nghiệm đúng với mọi khi và chỉ khi?
.
.
.
.
