Quiz

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 4

Admin49 câu hỏiToánLớp 12

49 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 2x - x² và y = 0. Vật thể tròn xoay được sinh ra bởi hình phẳng (H) khi nó quay quanh trục Ox có thể tích bằng

A. $\frac{16 π}{15};$

B. $\frac{17 π}{15};$

C. $\frac{18 π}{15};$

D. $\frac{19 π}{15} .$

2. Nhiều lựa chọn

Kí hiệu z₁; z₂ là hai nghiệm của phương trình z² + z + 1 = 0. Tính P = z₁² + z₂²+ z₁z₂.

A. P = 2;

B. P = -1;

C. P = 0;

D. P = 1.

3. Nhiều lựa chọn

Trong không gian Oxyz, gọi m, n là hai giá trị thực thỏa mãn giao tuyến của hai mặt phẳng(P_m): mx + 2y + nz + 1 = 0 và (Q_m): x - my + nz + 2 = 0 cùng vuông góc với mặt phẳng(a): 4x - y - 6z + 3 = 0. Khi đó ta có

A. m + n = 0;

B. m + n = 2;

C. m + n = 1;

D. m + n = 3.

4. Nhiều lựa chọn

Trên khoảng (0; +¥), họ nguyên hàm của hàm số $f (x) = x^{\frac{5}{2}}$ là:

A. $\int f (x) d x = \frac{7}{2} x^{\frac{7}{2}} + C;$

B. $\int f (x) d x = \frac{2}{7} x^{\frac{7}{2}} + C;$

C. $\int f (x) d x = \frac{3}{2} x^{\frac{3}{2}} + C;$

D. $\int f (x) d x = \frac{2}{3} x^{\frac{3}{2}} + C .$

5. Nhiều lựa chọn

Nếu $\int f (x) d x = \frac{1}{x^{2}} + \ln x + C$ thì f (x) là

A. $f (x) = \frac{2}{x^{3}} + \frac{1}{x};$

B. $f (x) = \frac{- 1}{x^{4}} + \frac{1}{x};$

C. $f (x) = \frac{x^{2} - 2}{x^{3}};$

D. $f (x) = \frac{- 2}{x^{3}} - \frac{1}{x} .$

6. Nhiều lựa chọn

Cho hàm số f (x) xác định và liên tục trên ℝ. Gọi S là diện tích hình phẳng giới hạn bởi các đườngy = f (x), y =0, x= -2 và x = 3 (như hình vẽ). Khẳng định nào dưới đây đúng?

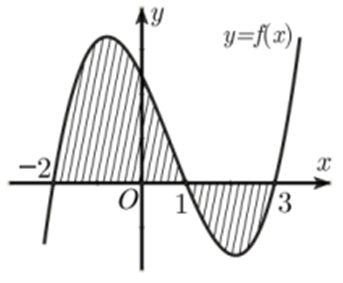
Media VietJack

A. $S = - \int_{- 2}^{1} f (x) d x - \int_{1}^{3} f (x) d x;$

B. $S = \int_{- 2}^{1} f (x) d x - \int_{1}^{3} f (x) d x;$

C. $S = - \int_{- 2}^{1} f (x) d x + \int_{1}^{3} f (x) d x;$

D. $S = \int_{- 2}^{1} f (x) d x + \int_{1}^{3} f (x) d x .$

7. Nhiều lựa chọn

Môđun của số phức z = -2 + 4i bằng

A. 4;

B. 2;

C. $\sqrt{5};$

D. $2 \sqrt{5} .$

8. Nhiều lựa chọn

Nếu $\int_{2}^{5} f (x) d x = 3$ thì $\int_{2}^{5} 4 f (x) d x$ bằng

A. 12;

B. 7;

C. 1;

D. 4.

9. Nhiều lựa chọn

Cho hàm số y =f (x) có đạo hàm là f '(x) = 12x² + 2, "x Î ℝ và f (-1) = 3. Biết F (x) là nguyên hàmcủa f (x) thỏa mãn F (-2) = 2, khi đó F(1) bằng

A. 15;

B. 11;

C. 6;

D. 1.

10. Nhiều lựa chọn

Nếu $\int_{2}^{5} f (x) d x = 3$ và $\int_{2}^{5} g (x) d x = - 2$ thì $\int_{2}^{5} [f (x) - g (x)] d x$ bằng

A. 5;

B. -5;

C. 1;

D. 3.

11. Nhiều lựa chọn

Cho hàm số f (x) = x + cos x. Khẳng định nào dưới đây đúng?

A. $\int f (x) d x = \frac{x^{2}}{2} + \sin x + C;$

B. $\int f (x) d x = \frac{x^{2}}{2} - \sin x + C;$

C. $\int f (x) d x = 1 + \sin x + C;$

D. $\int f (x) d x = \frac{x^{2}}{2} + \frac{\cos^{2} x}{2} + C .$

12. Nhiều lựa chọn

Nếu $\int_{1}^{3} f (x) d x = 2$ thì $\int_{1}^{3} [3 f (x) - 2 x] d x$ bằng

A. 4;

B. -2;

C. 2;

D. -4.

13. Nhiều lựa chọn

Trong không gian Oxyz, đường thẳng $d : \{\begin{matrix} x = 1 + 2 t \\ y = 2 - 2 t \\ z = - 3 - 3 t \end{matrix}$ qua điểm nào dưới đây?

A. Điểm Q(2;2;3);

B. Điểm N(2; -2; -3);

C. Điểm M(1;2; -3);

D. Điểm P(1;2;3).

14. Nhiều lựa chọn

Trong không gian Oxyz, cho điểm A(-4; -3;3) và mặt phẳng (P): 2x + 6y - 2z - 1 = 0. Đường thẳngđi qua A và vuông góc với (P) có phương trình là

A. $\frac{x - 4}{1} = \frac{y - 3}{3} = \frac{z + 3}{- 1};$

B. $\frac{x + 4}{1} = \frac{y + 3}{3} = \frac{z - 3}{- 1};$

C. $\frac{x + 4}{1} = \frac{y + 3}{3} = \frac{z - 3}{1};$

D. $\frac{x - 4}{1} = \frac{y - 3}{3} = \frac{z + 3}{1} .$

15. Nhiều lựa chọn

Diện tích hình phẳng giới hạn bởi hai đường y = x²-4 và y = 2x -4 bằng

A. 36;

B. $\frac{4}{3};$

C. $\frac{4 π}{3};$

D. 36p.

16. Nhiều lựa chọn

Trong không gian Oxyz, cho hai điểm A(-1;2;0) và B(3;0;2). Mặt phẳng trung trực của đoạn thẳngAB có phương trình là

A. x + y + z - 3 = 0;

B. 2x - y + z + 2 = 0;

C. 2x + y + z - 4 = 0;

D. 2x - y + z - 2 = 0.

17. Nhiều lựa chọn

Trong không gian Oxyz, cho hai điểm A(2;4;1); B(-1;1;3) và mặt phẳng (P): x - 3y + 2z - 5 = 0.Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình dạngax + by + cz - 11 = 0. Khi đó a + b + c bằng

A. 5;

B. 15;

C. -5;

D. -15.

18. Nhiều lựa chọn

Trong không gian Oxyz, cho mặt phẳng (Q) song với mặt phẳng (P): 2x - 2y + z- 7 = 0. Biết mặtphẳng (Q) cắt mặt cầu (S): x² + (y - 2)² + (z + 1)² = 25 theo một đường tròn có bán kính r = 3. Khi đó mặtphẳng (Q) có phương trình là

A. x - y + 2z - 7 = 0;

B. 2x - 2y + z - 7 = 0;

C. 2x - 2y + z - 17 = 0;

D. 2x - 2y + z + 17 = 0.

19. Nhiều lựa chọn

Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị của hàm sốy = f (x), trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích của khối tròn xoay tạo thành khiquay D quanh trục hoành được tính theo công thức

A. $V = π \int_{a}^{b} f^{2} (x) d x;$

B. $V = π^{2} \int_{a}^{b} f^{2} (x) d x;$

C. $V = π^{2} \int_{a}^{b} f (x) d x;$

D. $V = 2 π \int_{a}^{b} f^{2} (x) d x .$

20. Nhiều lựa chọn

Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số $y = \frac{1}{\sqrt{x}}$ , trục hoành và hai đường thẳng x =1,x = 2. Thể tích V của khối tròn xoay tạo thành khi cho hình phẳng (H) quay quanh trục Ox bằng

A. pln 2;

B. $2 π (\sqrt{2} - 1);$

C. 2p;

D. ln 2.

21. Nhiều lựa chọn

Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3, biết rằng thiết diện của vậtthể bị cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x (0 £x£3) là hình chữ nhật có hai kíchthước là x và $\sqrt{9 - x^{2}}$ ?

A. 3;

B. 9;

C. 18;

D. 36.

22. Nhiều lựa chọn

Cho số phức z = 6 -2i, khi đó 2z bằng

A. 12 - 4i;

B. 12 - 2i;

C. 3 - i;

D. 6 - 4i.

23. Nhiều lựa chọn

Trên mặt phẳng tọa độ, cho M (2; -3) là điểm biểu diễn của số phức z. Phần ảo của z bằng

A. 2;

B. 3;

C. -3;

D. -2.

24. Nhiều lựa chọn

Số phức liên hợp của số phức z = 3 -2i là

A. $\bar{z} = 3 + 2 i;$

B. $\bar{z} = 2 - 3 i;$

C. $\bar{z} = - 3 + 2 i;$

D. $\bar{z} = - 3 - 2 i .$

25. Nhiều lựa chọn

Cho số phức z thoả mãn $\frac{z}{3 + 2 i} = 1 - i$ . Phần thực của z bằng

A. -1;

B. 1;

C. 5;

D. -5.

26. Nhiều lựa chọn

Cho số phức z thỏa mãn (1 + i)z = 14 - 2i. Số phức liên hợp $\bar{z}$ của số phức z là

A. $\bar{z} = 8 - 6 i;$

B. $\bar{z} = 8 + 6 i;$

C. $\bar{z} = 6 - 8 i;$

D. $\bar{z} = 6 + 8 i .$

27. Nhiều lựa chọn

Cho số phức z = a + bi (a, b Î ℝ, a > 0) thỏa mãn |z - 1 + 2i| = 5 và $z . \bar{z} = 10.$ Khi đó P = a - b có giátrị bằng

A. P = 4;

B. P = -4;

C. P = -2;

D. P = 2.

28. Nhiều lựa chọn

Trong không gian Oxyz, mặt phẳng qua ba điểm A(0;0;1), B(0;2;0), C(-4;0;0) có phương trình là

A. $\frac{x}{1} + \frac{y}{2} + \frac{z}{- 4} = 0;$

B. $\frac{x}{- 4} + \frac{y}{2} + \frac{z}{1} = 1;$

C. $\frac{x}{1} + \frac{y}{2} + \frac{z}{4} = 0;$

D. $\frac{x}{1} + \frac{y}{2} + \frac{z}{4} = 1.$

29. Nhiều lựa chọn

Nghiệm phức có phần ảo âm của phương trình z² - 2z + 10 = 0 là:

A. 1 + 3i;

B. -1 + 3i;

C. -1 - 3i;

D. 1 - 3i.

30. Nhiều lựa chọn

Gọi z₁ và z₂ là hai nghiệm phức của phương trình z² - z + 3 = 0. Khi đó |z₁|+| z₂| bằng

A. -5;

B. $2 \sqrt{3};$

C. 3;

D. 1.

31. Nhiều lựa chọn

Gọi z₀ là nghiệm phức có phần ảo dương của phương trình z² - 4z + 13 = 0. Trên mặt phẳng tọa độ,điểm biểu diễn của số phức z₀ là

A. M(2;3);

B. P(-2;3);

C. Q(3;2);

D. N (-3;2).

32. Nhiều lựa chọn

Kí hiệu z₁, z₂ là hai nghiệm phức của phương trình z² - 2z + 6 = 0. Biểu thức $P = \frac{1}{z_{1}} + \frac{1}{z_{2}}$ bằng

A. $\frac{1}{3};$

B. $- \frac{1}{6};$

C. 6;

D. 3.

33. Nhiều lựa chọn

Phương trình z² + a.z + b = 0, với a, b là các số thực nhận số phức 1 - i là một nghiệm. Khi đó a - b bằng

A. -2;

B. -4;

C. 4;

D. 0.

34. Nhiều lựa chọn

Trong không gian Oxyz, mặt phẳng (P): 2x - 6y + 4z - 1 = 0 có một vectơ pháp tuyến là:

A. $\vec{n} = (1; - 3; 2);$

B. $\vec{n} = (1; 2; 3);$

C. $\vec{n} = (2; 6; 4);$

D. $\vec{n} = (4; - 6; 2) .$

35. Nhiều lựa chọn

Trong không gian Oxyz , cho hai điểm A(1; 1; 2), B(-1; 3; -9). Tọa độ điểm M thuộc Oy sao cho DABM vuông tại A là

A. M(0; 11; 0);

B. M(0; -11; 0);

C. M(0; -1; 0);

D. M(0; 1; 0).

36. Nhiều lựa chọn

Trong không gian Oxyz, cho hai vectơ $\vec{u} = (1; 3; - 2)$ và $\vec{v} = (2; 1; - 1)$ . Tọa độ của vectơ $\vec{u} + \vec{v}$ là

A. (3; 4; -3);

B. (-1; 2; -3);

C. (-1; 2; -1);

D. (1; -2; 1).

37. Nhiều lựa chọn

Trong không gian Oxyz, tọa độ một vectơ vuông góc với cả hai vectơ $\vec{a} = (1; 1; - 2)$ và $\vec{b} = (3; - 2; - 1)$ là

A. (1; 1; -1);

B. (1; 1; 1);

C. (1; -1; -1);

D. (-1; 1; -1).

38. Nhiều lựa chọn

Trong không gian Oxyz, cho 4 điểm A(2; 0; 2), B(1; -1; -2), C(-1;1 ; 0), D(-2; 1; 2). Thể tích của khối tứ diện ABCD bằng

A. 14;

B. $\frac{14}{3};$

C. 7;

D. $\frac{7}{3} .$

39. Nhiều lựa chọn

Trong không gian Oxyz, cho hai điểm A(-2; 3; 1) và B(5; 6; 2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tỉ số $\frac{A M}{B M}$ bằng

A. $\frac{1}{2};$

B. 2;

C. $\frac{1}{3};$

D. 3.

40. Nhiều lựa chọn

Trong không gian Oxyz, mặt cầu (S): (x + 1)² + (y - 2)² + z² = 9 có bán kính bằng

A. 3;

B. 81;

C. 9;

D. 6;

41. Nhiều lựa chọn

Trong không gian Oxyz, cho bốn đường thẳng:

$(d_{1}) : \frac{x - 3}{1} = \frac{y + 1}{- 2} = \frac{z + 1}{1},$ $(d_{2}) : \frac{x}{1} = \frac{y}{- 2} = \frac{z - 1}{1}, (d_{3}) : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z - 1}{1}, (d_{4}) : \frac{x}{1} = \frac{y - 1}{- 1} = \frac{z - 1}{1} .$

Gọi D là đường thẳng cắt cả bốn đường thẳng trên, phươngtrình đường thẳng D là:

A. $\frac{x - 3}{2} = \frac{y + 4}{- 3} = \frac{z - 2}{1};$

B. $\frac{x - 3}{2} = \frac{y - 4}{- 3} = \frac{z - 2}{1};$

C. $\frac{x + 3}{2} = \frac{y + 4}{- 3} = \frac{z - 2}{1};$

D. $\frac{x - 3}{2} = \frac{y + 4}{- 3} = \frac{z + 2}{1} .$

42. Nhiều lựa chọn

Trong không gian Oxyz, cho hai điểm A(3; -2; 6), B(0; 1;0) và mặt cầu(S): (x - 1)² + (y - 2)² + (z - 3)² = 25. Mặt phẳng (P): ax + by + cz - 2 = 0 đi qua A, B và cắt mặt cầu (S) theogiao tuyến là đường tròn có bán kính nhỏ nhất. Biểu thức T = a + b + c có giá trị bằng

A. 3;

B. 5;

C. 2;

D. 4.

43. Nhiều lựa chọn

Cho hàm số f (x) xác định trên ℝ\ {-1;1} thỏa mãn $f' (x) = \frac{1}{x^{2} - 1}$ . Biết f (3) + f (-3) = 4 và $f (\frac{1}{3}) + f (- \frac{1}{3}) = 2$ . Giá trị của biểu thức f (-5) + f (0) + f (2) bằng:

A. $5 - \frac{1}{2} \ln 2;$

B. $6 - \frac{1}{2} \ln 2;$

C. $5 + \frac{1}{2} \ln 2;$

D. $6 + \frac{1}{2} \ln 2.$

44. Nhiều lựa chọn

Cho hàm số f (x) có đạo hàm liên tục trên ℝ và f (x³ - 3x² + 3x) = 2x + 2. Khi đó $\int_{1}^{9} x . f' (x) d x$ bằng

A. 68;

B. $\frac{68}{3};$

C. $\frac{136}{3};$

D. 12.

45. Nhiều lựa chọn

Cho hàm số y = f (x) liên tục trênℝ và có đồ thị của hàm số f '(x) như hình bên dưới. Khẳng địnhnào sau đây đúng?

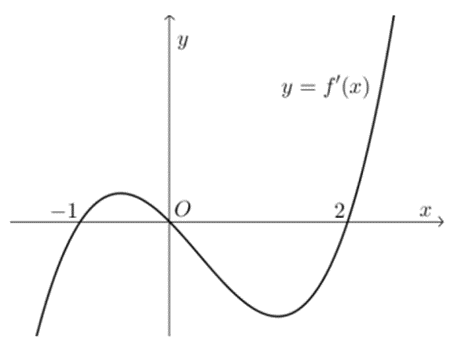
Media VietJack

A. f (0) > f (2) > f (-1);

B. f (0) > f (-1) > f (2);

C. f (2) > f (0) > f (-1);

D. f (-1) > f (0) > f (2).

46. Nhiều lựa chọn

Cho hàm số y = f (x) có đồ thị như hình vẽ và diện tích hai phần A; B lần lượt bằng 11; 2. Giá trị của $I = \int_{- 1}^{0} f (3 x + 1) d x$ bằng

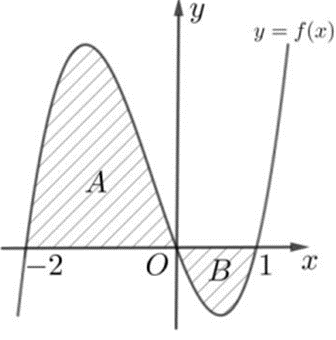
Media VietJack

A. 3;

B. $\frac{13}{3};$

C. 9;

D. 13.

47. Nhiều lựa chọn

Hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục đốixứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng

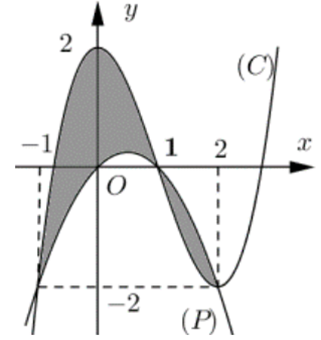
Media VietJack

A. $\frac{37}{12};$

B. $\frac{7}{12};$

C. $\frac{11}{12};$

D. $\frac{9}{4} .$

48. Nhiều lựa chọn

Gọi S là tập hợp tất cả các số phức z sao cho số phức $w = \frac{1}{|z| - z}$ có phần thực bằng $\frac{1}{12}$ . Xét cácsố phức z₁, z₂Î S thỏa mãn |z₁-z₂| = 6, giá trị nhỏ nhất của P = |z₁- 10|² - |z₂-10|² bằng