Quiz

Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 15

Admin50 câu hỏiToánLớp 12

50 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Trong không gianvới hệtọađộOxyz, đườngthẳng(△): $\frac{x - 1}{2}$ = $\frac{y + 2}{1}$ = $\frac{z}{- 1}$ đi qua điểm nào dưới đây?

A.(1;−3; 1).

B.(1; −2; 0).

C.(2;l;−1).

D. (3;−1; 1).

2. Nhiều lựa chọn

ThểtíchV của khối tròn xoay tạo thành do hình phẳng giới hạn bởi đồ thị hàm sốy =f(x),trụchoànhvàđườngthẳngx= b (phầntôđậm tronghìnhvẽ)quay quanh trụcOxđược tính theocôngthức nào dưới đây?

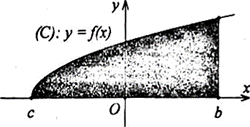
Media VietJack

A. V = $\int_{b}^{c} {[f (x)]}^{2} d x$ .

B. V = $\int_{c}^{b} |f (x)| d x$ .

C. V = π $\int_{c}^{b} {[f (x)]}^{2} d x$ .

D. V = π. $\int_{b}^{c} {[f (x)]}^{2} d x$ .

3. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz,cho =(2;−1;3).Tọa độ của vectơ 2 $\vec{a}$ là

A.(4;−2;3).

B.(4;−1;3).

C.(4;−2; 6).

D.(4;−2;5).

4. Nhiều lựa chọn

Trênmặtphẳngtọađộ,cho sốphứczcóđiểmbiểudiễnlà M (3; −4).Sốphức nghịchđảocủasốphứcz1à

A. $\frac{1}{z}$ = $\frac{1}{3}$ − $\frac{1}{4}$ i.

B. $\frac{1}{z}$ =− $\frac{3}{25}$ + $\frac{4}{25}$ i.

C. $\frac{1}{z}$ = $\frac{3}{25}$ − $\frac{4}{25}$ i.

D. $\frac{1}{z}$ = $\frac{3}{25}$ + $\frac{4}{25}$ i.

5. Nhiều lựa chọn

Trênmặtphẳngtọa độ,điểmnàotronghìnhvẽbênlàđiểmbiểudiễnsốphức z = 2 – i?

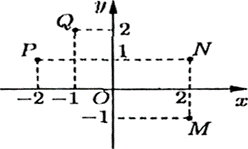
Media VietJack

A.Q.

B. P.

C. M.

D. N.

6. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x + 3y − 4z + 7 = 0. Vectơ pháp tuyến của mặt phẳng (P) 1à

A. $\vec{n}$ =(−2;3;−4).

B. $\vec{n}$ = (2;3;−4).

C. $\vec{n}$ =(2;−3;−4).

D. $\vec{n}$ =(−2; −3; −4).

7. Nhiều lựa chọn

Trong khônggianvớihệtọađộ Oxyz,chohaimặtphẳng(α):3x+2y −z+1 =0và (α'):3x+2y−z−1=0.Vịtrítươngđốicủahaimặtphẳng(α)và(α ')là

A. vuông gócvớinhau.

B. songsongvớinhau.

C. trùngnhau.

D. cắt nhau nhưng không vuông góc với nhau.

8. Nhiều lựa chọn

Chohaisố phúcz₁ =5 –6i vàz₂ = 2+ 3i.Số phức3z₁ −4z₂ bằng:

A.7−30i.

B.−14 +33i.

C.26−l5i.

D.23−6i.

9. Nhiều lựa chọn

Chohàm số f (x) liên tục trên tập ℝ, F (x) là một nguyên hàm của f (x) thỏa mãn F (1) = 3 và F (0) = 1. Giá trị $\int_{0}^{1} f (x) d x$ bằng

A. 4.

B. 2.

C. −3.

D. −4.

10. Nhiều lựa chọn

Cho hai số phức z₁ = 2i, z₂ = 3 – 2i. Tìm số phức w = $\frac{z_{1}}{z_{2}}$

A.w = $\frac{5}{13}$ – $\frac{12}{13}$ i.

B.w = $\frac{3}{7}$ – $\frac{4}{7}$ i.

C. w = $\frac{5}{13}$ + $\frac{12}{13}$ i.

D.w = – $\frac{5}{13}$ –i.

11. Nhiều lựa chọn

Trongkhônggianvớihệtọađộ Oxyz,chođường thẳng (d): $\frac{x + 1}{1}$ = $\frac{y - 2}{3}$ = $\frac{z}{- 2}$ ,vectơnàodướiđâylàvectơchỉphươngcủađườngthẳng(d)?

A. $\vec{u}$ = (1; 3; 2).

B. $\vec{u}$ = (1; 3; –2).

C. $\vec{u}$ = (1; –3; –2).

D. $\vec{u}$ = (–1; 3; –2).

12. Nhiều lựa chọn

Trong không gian với hệ tọađộ Oxyz,đườngthẳngđiquahaiđiểmM (1; –2; 0)và N (3; 1; 1)cómộtvectơchỉphươnglà

A. $\vec{u_{1}}$ =(4; 1;1).

B. $\vec{u_{3}}$ =(2;3;l).

C. $\vec{u_{2}}$ =(–2;–3;1)

D. $\vec{u_{4}}$ =(2;–3; 1).

13. Nhiều lựa chọn

Chohaisốphúcz₁=1+i vàz₂=1+2i.Phầnảocủasốphứcw= z₁.z₂là

A.1.

B.2.

C.3.

D. –1.

14. Nhiều lựa chọn

Cho $\int_{- 2}^{2} f (x) d x$ = 2, $\int_{2}^{5} f (x) d x$ =–4. Tính I = $\int_{- 2}^{5} f (x) d x$ .

A. I = 6.

B. I = –6.

C. I = 2.

D. I = –2.

15. Nhiều lựa chọn

TínhI= $\int_{0}^{1} x . e^{x} d x$ .

A. I = e.

B. I = e – 1.

C. I = 1.

D. I = 2e – 1.

16. Nhiều lựa chọn

Họnguyênhàmcủahàmsốf (x) = x² là

A. – $\frac{x^{2}}{2}$ + C.

B. 2x + C.

C. x³ + C.

D. $\frac{x^{3}}{3}$ + C.

17. Nhiều lựa chọn

Chosốphứcz=5+7i. Xácđịnhphầnthựcvàphần ảocủasốphứcz.

A. Phầnthựcbằng5vàphầnảobằng7i.

B. Phầnthựcbằng 5và phầnảo bằng –7.

C. Phần thực bằng 5 và phần ảo bằng 7.

D. Phần thực bằng 7 và phần ảo bằng 5.

18. Nhiều lựa chọn

Cho f (x) là hàm số liên tục trên đoạn [2; 5]. Nếu F (x) là một nguyên hàm của hàm số f (x) trên đoạn [2; 5] thì $\int_{2}^{5} f (x) d x$ bằng

A.f (5) – f (2).

B.F (2)– F (5).

C. F (2) + F (5).

D.F (5) – F (2).

19. Nhiều lựa chọn

Mệnh đềnàodướiđâysai?

A. $\int f' (x) d x$ =f (x) + C với mọi hàm f (x) có đạo hàm trên ℝ.

B. $\int k f (x) d x$ = k $\int f (x) d x$ với mọi hằng số k và với mọi hàm số f (x) có đạo hàm trên ℝ.

C. $\int [f (x) - g (x)] d x$ = $\int f (x) d x$ – $\int g (x) d x$ với mọi hàm f (x), g (x) có đạo hàm trên ℝ.

D. $\int [f (x) + g (x)] d x$ = $\int f (x) d x$ + $\int g (x) d x$ với mọi hàm f (x), g (x) có đạo hàm trên ℝ.

20. Nhiều lựa chọn

Môđuncủa sốphứcz= –5+2ibằng:

A.29.

B.7.

C.3.

D. $\sqrt{29}$

21. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, cho hai vectơ $\vec{u}$ = (1; –2; 3), $\vec{v}$ = (0; –1; 2). Tích vô hướng của hai vectơ $\vec{u}$ và $\vec{v}$ bằng

A. $\vec{u} . \vec{v}$ = (0; 2; 6).

B. $\vec{u} . \vec{v}$ = 8.

C. $\vec{u} . \vec{v}$ = (–1; 1; –1).

D. $\vec{u} . \vec{v}$ =9.

22. Nhiều lựa chọn

Chosốphứcz=2(4–3i).Trongcáckhẳngđịnhdưới đây,khẳng định nào sai?

A. Môđun của z bằng 10.

B. Sốphức zcó phần thực bằng 8, phần ảo bằng 6i.

C. Sốphức zcó phần thực bằng 8, phần ảo bằng –6.

D. Sốphứcliênhợpcủazlà $\bar{z}$ =8+6i.

23. Nhiều lựa chọn

Chosố phứczthỏamãn(2i + 1)z+10i=5.Khiđózbằng:

A. –3–4i.

B.3+4i.

C.–2– i.

D.–2 + i.

24. Nhiều lựa chọn

TrongtậpsốphứcC.Phươngtrìnhbậchainào dưới đây nhậnhaisố phức 2 – 3i và 2 + 3i làm nghiệm?

A.z² + 4z + 13 = 0.

B.z² + 4z + 3 = 0.

C.z² – 4z + 3 =0.

D.z² – 4z + 13 =0.

25. Nhiều lựa chọn

Chotíchphân I = $\int_{1}^{e} \frac{3 \ln x + 1}{x} d x$ .Nếuđặt t = lnx thì

A.I = $\int_{0}^{1} \frac{3 t + 1}{e^{t}} d t$ .

B. I = $\int_{1}^{e} (3 t + 1) d t$ .

C. I = $\int_{0}^{1} (3 t + 1) d t$ .

D. I = $\int_{1}^{e} \frac{3 t + 1}{t} d t$ .

26. Nhiều lựa chọn

Trongkhônggianvớihệ tọađộ Oxyz, chomặtcầu (S): x² +y² + z² – 2x + 6y – 8z+ 1 = 0. Tọa độ tâm I và bán kính R của mặt cầu (S) là:

A. I (2; –6; 8), R = $\sqrt{103}$ .

B. I (–1; 3; –4), R = 5.

C. I (1; –3; 4), R = 5.

D. I (1; –3; 4), R = 25.

27. Nhiều lựa chọn

Trong không gian với hệ tọađộ Oxyz,chomặtphẳng(P):x+2y –2z–2=0vàđiểmI (1;2;–3). Bánkính củamặtcầu có tâm I và tiếp xúc với mặt phẳng (P) bằng

A. $\frac{11}{3}$ .

B. 1.

C. 3.

D. $\frac{1}{3}$ .

28. Nhiều lựa chọn

Trongkhônggianvớihệtọađộ Oxyz,chohaiđường thẳng(d₁): $\{\begin{cases} x = 2 + 2 t \\ y = 1 - t \\ z = 3 + t \end{cases}$ và (d₂): $\{\begin{cases} x = 2 + 2 t' \\ y = - 1 - t' \\ z = 3 + t' \end{cases}$ . Vị trí tương đối của hai đường thẳng (d₁) và (d₂) là

A. chéo nhau.

B.trùngnhau.

C. songsong.

D.cắtnhau.

29. Nhiều lựa chọn

Tìm họ nguyên hàm của hàm số f (x) = cosx.

A. $\int \cos x d x$ =– $\frac{1}{2}$ sinx + C.

B. $\int \cos x d x$ = sinx + C.

C. $\int \cos x d x$ = sin2x + C.\

D. $\int \cos x d x$ =–sinx + C.

30. Nhiều lựa chọn

Diệntíchhìnhphẳng giớihạnbởiđồthịhàmsốy= x²– x vàtrụchoành là

A. $\frac{1}{6}$ π.

B. $\frac{1}{6}$ .

C. $\frac{1}{36}$ .

D. – $\frac{1}{6}$ .

31. Nhiều lựa chọn

Chosốphứcz=3 –4i.Phầnthựcvà phần ảocủasốphức $\bar{z}$ lần lượt là

A.3 và –4.

B. –4 và 3.

C. 3 và –4i.

D. 3 và 4.

32. Nhiều lựa chọn

Chosốphứczthỏamãn(2 + i)z=9–8i.Môđuncủasốphứczbằng

A.29.

B. $\sqrt{21}$ .

C. $\sqrt{29}$ .

D. $\sqrt{7}$ .

33. Nhiều lựa chọn

Tính tích phân I = $\int_{1}^{2} (2 x - 1) d x$

A. I=3.

B. I =2.

C. I = 1.

D. I = $\frac{5}{6}$ .

34. Nhiều lựa chọn

Tíchphân $\int_{0}^{\frac{π}{2}} e^{\cos x} . \sin x d x$ bằng:

A.1 – e.

B. e + 1.

C. e.

D. e – 1.

35. Nhiều lựa chọn

Cho hình phẳng (H) giới hạn bởi các đường y = x²+ 2,y=0, x = 1,x=2.Gọi V là thể tích của khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox.Mệnh đề nào dưới đây đúng?

A.V = $\int_{1}^{2} {(x^{2} + 2)}^{2} d x$ .

B. V = $\int_{1}^{2} (x^{2} + 2) d x$ .

C. V = π $\int_{1}^{2} (x^{2} + 2) d x$ .

D. V =π $\int_{1}^{2} {(x^{2} + 2)}^{2} d x$ .

36. Nhiều lựa chọn

Số phức z thỏa mãn 2z – 3(1 + i) = iz + 7 – 3i là

A. z = $\frac{14}{5}$ + $\frac{8}{5}$ .

B. z = 4 – 2i.

C. z = $\frac{14}{5}$ – $\frac{8}{5}$ .

D. z = 4 + 2i.

37. Nhiều lựa chọn

Cho biết $\int_{0}^{\frac{π}{2}} (4 - s inx) d x$ = aπ + b, với a, b là các số nguyên. Giá trị của biểu thức a + b bằng:

A. 1.

B. – 4.

C. 6.

D. 3.

38. Nhiều lựa chọn

Trongkhônggianvớihệtọađộ Oxyz,gọi(P)làmặt phẳng chứa đường thẳng (d): $\frac{x - 2}{1}$ = $\frac{y - 1}{2}$ = $\frac{z}{- 1}$ và cắt các trục Ox, Oy lần lượt tại A và B sao cho đường thẳng AB vuông góc với (d). Phương trình của mặt phẳng (P) là:

A. 2x – y – 3 = 0.

B. x + 2y + 5z – 4 = 0.

C. x + 2y – z – 4 = 0.

D. x + 2y + 5z – 5 = 0.

39. Nhiều lựa chọn

Cho hàm số f (x) có đạo hàm liên tục trên ℝ, đồng thời thỏa mãn $\int_{0}^{2} (f (x) + 3 x^{2}) d x$ = 10. Tích phân $\int_{0}^{2} f (x) d x$ bằng:

A.18.

B. 2.

C. –2.

D. –18.

40. Nhiều lựa chọn

Chosốphứcz=a+ bi,(a, b ∈ ℝ)thỏa mãnz+ 1 +3i–|z|i=0.TínhS= a +3b.

A. S = $\frac{7}{3}$ .

B. S =–5.

C. S = 5.

D. S =– $\frac{7}{3}$

41. Nhiều lựa chọn

Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y = ex và hai đường thẳng x = 0, x = 1 . Thể tích của khối tròn xoay tạo thành khi quay (H) xung quanh trục Ox là

A. $\frac{π}{2}$ (e² – 1).

B. π (e² – 1).

C. $\frac{π}{2}$ (e² + 1).

D. π (e² +1).

42. Nhiều lựa chọn

Trongkhônggianvớihệ tọa độ Oxyz,chobađiểmA (0; 1; 0), B (2; 2; 2), C (–2; 3; 1)vàđường thẳng (d): $\frac{x - 1}{2}$ = $\frac{y + 2}{- 1}$ = $\frac{z - 3}{2}$ .TìmđiểmMthuộc (d) để thể tích V của tứ diện M.ABC bằng 3.

A. M $(- \frac{15}{2}; \frac{9}{4}; - \frac{11}{2})$ ; M $(- \frac{3}{2}; - \frac{3}{4}; \frac{1}{2})$ .

B. M $(- \frac{3}{5}; - \frac{3}{4}; \frac{1}{2})$ ; M $(- \frac{15}{2}; \frac{9}{4}; \frac{11}{2})$ .

C. M $(\frac{3}{2}; - \frac{3}{4}; \frac{1}{2})$ ; M $(\frac{15}{2}; \frac{9}{4}; \frac{11}{2})$ .

D. M $(\frac{3}{5}; - \frac{3}{4}; \frac{1}{2})$ ; M $(\frac{15}{2}; \frac{9}{4}; \frac{11}{2})$ .

43. Nhiều lựa chọn

Trênmặtphẳngtọađộ,chosốphứcz=– 1 – 4i.Điểm nào sau đây là điểm biểu diễn của số phức z – $\bar{z}$ ?

A. M (–2; 0).

B. M (0; –2).

C. M (–8; 0).

D. M (0; –8).

44. Nhiều lựa chọn

Trongkhônggianvớihệ tọa độ Oxyz,biết mặt phẳng (P): ax + by + cz – 27 = 0, (a, b, c ∈ ℝ, a² +b²+c² ≠ 0) đi qua hai điểm A (3; 2; 1), B (–3; 5; 2) và vuông góc với mặt phẳng (Q): 3x + y + z + 4 = 0. Tính tổng S = a + b + c.

A. S =–4.

B. S =–2.

C. S =–12.

D. S = 2.

45. Nhiều lựa chọn

Trong không gian vớihệtọa độ Oxyz,choba đường thẳng (d₁): $\frac{x - 3}{2}$ = $\frac{y + 1}{1}$ = $\frac{z - 2}{- 2}$ , (d₂): $\frac{x + 1}{3}$ = $\frac{y}{- 2}$ = $\frac{z + 4}{- 1}$ và (d₃): $\frac{x + 3}{4}$ = $\frac{y - 2}{- 1}$ = $\frac{z}{6}$ . Đường thẳng song song với (d₃), cắt (d₁) và (d₂) có phương trình là

A. $\frac{x - 1}{4}$ = $\frac{y}{- 1}$ = $\frac{z + 4}{6}$ .

B. $\frac{x - 3}{- 4}$ = $\frac{y + 1}{1}$ = $\frac{z - 2}{- 6}$ .

C. $\frac{x - 3}{4}$ = $\frac{y + 1}{1}$ = $\frac{z - 2}{6}$ .

D. $\frac{x + 1}{4}$ = $\frac{y}{- 1}$ = $\frac{z - 4}{6}$ .

46. Nhiều lựa chọn

Cho đồ thị (C):y= f(x)= $\sqrt{x}$ .Gọi (H)là hìnhphẳnggiớihạnbởiđồ thị(C), đường thẳng x =9và trục Ox.ChođiểmMthuộcđồ thị (C) và điểm A(9;0). Gọi V₁là thể tích khối tròn xoay khi cho (H) quay quanh trụcOx,V₂làthể tích khối trònxoaykhicho tamgiácAOMquay quanhtrụcOx. Biết rằng V₁=2 V₂. Tính diệntíchSphần hình phẳng giới hạn bởi đồ thị (C) và đường thẳng OM.

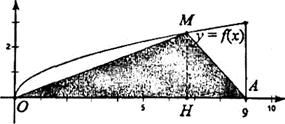
Media VietJack

A.S = $\frac{4}{3}$ .

B. S = $\frac{27 \sqrt{3}}{16}$ .

C. S = 3.

D. S = $\frac{3 \sqrt{3}}{2}$ .

47. Nhiều lựa chọn

Xét các số phức z = a + bi, (a, b ∈ ℝ) thỏa mãn 4(z – $\bar{z}$ ) – 15i = i(z + $\bar{z}$ – 1)². Tính F = a + 4b khi $|z - \frac{1}{2} + 3 i|$ đạt giá trị nhỏ nhất.

A. F = 7.

B.F= 4.

C.F =5.

D. F =8.

48. Nhiều lựa chọn

Xét hàm số f (x) liên tục trên đoạn [0; 1] và thỏa mãn điều kiện 2f (x) – 3f (1 –x) = x $\sqrt{1 - x}$ . Tính tích phân I = $\int_{0}^{1} f (x) d x$ .

A. I = $\frac{4}{75}$ .

B. I =– $\frac{1}{15}$ .

C. I = $\frac{1}{25}$ .

D. I =– $\frac{4}{15}$ .

49. Nhiều lựa chọn

Trongkhônggian với hệ trục tọa độ Oxyz, cho mặt cầu (S):x² +y² + z² –4x +10y –2z– 6= 0. Cho m là số thực thỏa mãn giao tuyến của hai mặt phẳng lần lượt có phương trình y = m và x + z – 3= 0 tiếp xúc với mặt cầu (S). Tích tất cả các giá trị mà m có thể nhận được bằng:

A. –5.

B. –11.

C. –10.

D. –8.

50. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (3; 3; 1), B (0; 2; 1) và mặt phẳng (α): x + y + z – 7 = 0. Đường thẳng (d) nằm trên (α) sao cho mọi điểm của (d) cách đều hai điểm A, B có phương trình là

A. $\{\begin{cases} x = 2 t \\ y = 7 - 3 t \\ z = t \end{cases}$

B. $\{\begin{cases} x = - t \\ y = 7 - 3 t \\ z = 2 t \end{cases}$

C. $\{\begin{cases} x = t \\ y = 7 + 3 t \\ z = 2 t \end{cases}$

D. $\{\begin{cases} x = t \\ y = 7 - 3 t \\ z = 2 t \end{cases}$

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube