Đề kiểm tra Hàm số liên tục (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho hàm số \[f\left( x \right)\] xác định trên \[\left[ {a;b} \right]\]. Tìm mệnh đề đúng.
Nếu hàm số \[f\left( x \right)\] liên tục trên \[\left[ {a;b} \right]\] và \[f\left( a \right)f\left( b \right) > 0\] thì phương trình \[f\left( x \right) = 0\] không có nghiệm trong khoảng \[\left( {a;b} \right)\].
Nếu \[f\left( a \right)f\left( b \right) < 0\] thì phương trình \[f\left( x \right) = 0\] có ít nhất một nghiệm trong khoảng \[\left( {a;b} \right)\].
Nếu hàm số \[f\left( x \right)\] liên tục, tăng trên \[\left[ {a;b} \right]\] và \[f\left( a \right)f\left( b \right) > 0\] thì phương trình \[f\left( x \right) = 0\] không có nghiệm trong khoảng \[\left( {a;b} \right)\].
Nếu phương trình \[f\left( x \right) = 0\]có nghiệm trong khoảng \[\left( {a;b} \right)\] thì hàm số \[f\left( x \right)\] phải liên tục trên \[\left( {a;b} \right)\].
Cho hàm số \(y = f(x)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Mệnh đề nào dưới đây đúng?
Nếu \(f(a).f(b) > 0\) thì phương trình \(f(x) = 0\) không có nghiệm nằm trong \(\left( {a;b} \right)\).
Nếu \(f(a).f(b) < 0\) thì phương trình \(f(x) = 0\) có ít nhất một nghiệm nằm trong \(\left( {a;b} \right)\).
Nếu \(f(a).f(b) > 0\) thì phương trình \(f(x) = 0\) có ít nhất một nghiệm nằm trong \(\left( {a;b} \right)\).
Nếu phương trình \(f(x) = 0\) có ít nhất một nghiệm nằm trong \(\left( {a;b} \right)\) thì \(f(a).f(b) < 0\).
Cho đồ thị của hàm số \(y = f\left( x \right)\) như hình vẽ sau:
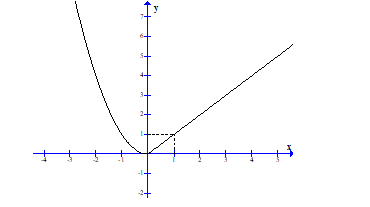
Chọn mệnh đề đúng.
Hàm số \(y = f\left( x \right)\) có đạo hàm tại điểm \(x = 0\) nhưng không liên tục tại điểm \(x = 0\).
Hàm số \(y = f\left( x \right)\)liên tục tại điểm \(x = 0\) nhưng không có đạo hàm tại điểm \(x = 0\).
Hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm tại điểm \(x = 0\).
Hàm số \(y = f\left( x \right)\) không liên tục và không có đạo hàm tại điểm \(x = 0\).
Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại \(x = 1\)?
A. 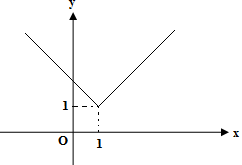 .
.
B. 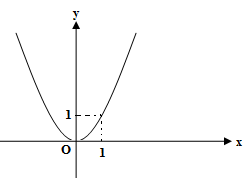 .
.
C. 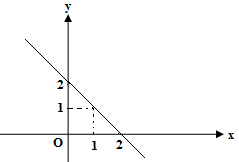 .
.
D. 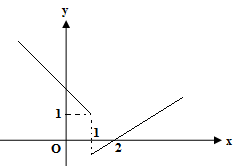 .
.
Nếu hàm số \(y = f\left( x \right)\) liên tục, đơn điệu trên \(\left[ {a;\,b} \right]\) và \(f\left( a \right).f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có nghiệm duy nhất.
Có đúng hai mệnh đề sai.
Cả ba mệnh đề đều đúng.
Cả ba mệnh đề đều sai.
Có đúng một mệnh đề sai.
Cho hàm số . Hãy chọn kết luận đúng
\(y\) liên tục phải tại \(x = 1\).
\(y\) liên tục tại \(x = 1\).
\(y\) liên tục trái tại \(x = 1\).
\(y\) liên tục trên \(\mathbb{R}\).
Hàm số nào sau đây liên tục tại \(x = 1\):
\(f\left( x \right) = \frac{{{x^2} + x + 1}}{{x - 1}}\).
\(f\left( x \right) = \frac{{{x^2} - x - 2}}{{{x^2} - 1}}\).
\(f\left( x \right) = \frac{{{x^2} + x + 1}}{x}\).
\(f\left( x \right) = \frac{{x + 1}}{{x - 1}}\).
Hàm số nào dưới đây gián đoạn tại điểm \({x_0} = - 1\).
\(y = \left( {x + 1} \right)\left( {{x^2} + 2} \right)\).
\(y = \frac{{2x - 1}}{{x + 1}}\).
\(y = \frac{x}{{x - 1}}\).
\(y = \frac{{x + 1}}{{{x^2} + 1}}\).
Hàm số nào sau đây gián đoạn tại \(x = 2\)?
\[y = \frac{{3x - 4}}{{x - 2}}\].
\[y = \sin x\].
\[y = {x^4} - 2{x^2} + 1\]
\[y = \tan x\].
Hàm số \[y = \frac{x}{{x + 1}}\] gián đoạn tại điểm \[{x_0}\] bằng?
\[{x_0} = 2018\].
\[{x_0} = 1\].
\[{x_0} = 0\]
\[{x_0} = - 1\].
Cho hàm số \(y = \left\{ \begin{array}{l}\frac{{{x^2} - 7x + 12}}{{x - 3}}\,\,\,\,{\rm{khi}}\,\,\,x \ne 3\\ - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x = 3\end{array} \right.\). Mệnh đề nào sau đây đúng?
Hàm số liên tục nhưng không có đạo hàm tại \({x_0} = 3\).
Hàm số gián đoạn và không có đạo hàm tại \({x_0} = 3\).
Hàm số có đạo hàm nhưng không liên tục tại \({x_0} = 3\).
Hàm số liên tục và có đạo hàm tại \({x_0} = 3\).
Cho hàm số Chọn mệnh đề đúng?
Hàm số liên tục tại \(x = 2\).
Hàm số gián đoạn tại \(x = 2\).
\(f\left( 4 \right) = 2\).
\(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 2\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\sin \pi x}&{{\rm{khi}}\,\,\left| x \right| \le 1}\\{x + 1\;}&{{\rm{khi}}\,\;\left| x \right| > 1}\end{array}} \right.\]. Các mệnh đề sau đúng/sai?
a) Hàm số liên tục trên \(\mathbb{R}\).
b) Hàm số liên tục trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
c) Hàm số liên tục trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
d) Hàm số gián đoạn tại \(x = \pm 1\).
Cho các hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{{x^2} - 4}}{{x - 2}}}&{{\rm{ khi }}x \ne 2}\\{4,5}&{{\rm{ khi }}x = 2}\end{array}} \right.\) và \(g(x) = \frac{2}{{x - 1}}\) . Khi đó:
a) Hàm số \(g(x)\) liên tục tại điểm \({x_0} = 2\).
b) Giới hạn \(\mathop {\lim }\limits_{x \to 2} f(x) = 4\)
c) Hàm số \(f(x)\) liên tục tại điểm \({x_0} = 2\).
d) Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại điểm \({x_0} = 2\).
Xét được tính liên tục của các hàm số sau trên tập xác định của nó:
a) \(f(x) = {x^3} - {x^2} + 8x\) là hàm số liên tục trên \(\mathbb{R}\).
b) \(f(x) = \frac{{{x^2}}}{{{x^2} - 3x}}\) là hàm số liên tục trên khoảng \(( - \infty ; + \infty )\).
c) \(f(x) = \frac{{\sin x + 1}}{{x + 1}}\) là hàm số liên tục trên các khoảng \(( - \infty ;0),(0; + \infty )\).
d) \(f(x) = \sqrt {x - 2} \) là hàm số liên tục trên nửa khoảng \([2; + \infty )\).
Cho các hàm số sau: \(f(x) = \left\{ {\begin{array}{*{20}{l}}{ - \frac{x}{2}{\rm{ khi }}x \le 1}\\{\frac{{{x^2} - 3x + 2}}{{{x^2} - 1}}{\rm{ khi }}x > 1}\end{array}} \right.\), \(g(x) = {x^2} - 3x + 1\) và \(h(x) = \sin \frac{{\pi x}}{4}\)
a) Hàm số \(f(x)\) liên tục tại điểm \({x_0} = 1\).
b) Hàm số \(g(x)\) liên tục tại điểm \({x_0} = 1\).
c) Hàm số \(h(x)\) không liên tục tại điểm \({x_0} = 2\).
d) Hàm số \(y = f\left( x \right).g\left( x \right)\) không liên tục tại điểm \({x_0} = 1\).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm giá trị của tham số \(m\) sao cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2{\rm{ n\~O u }}x \le 1}\\{mx + 1{\rm{ n\~O u }}x > 1}\end{array}} \right.\) liên tục tại \(x = 1\).
Tìm các khoảng trên đó hàm số \(f(x) = \frac{{\cos x}}{{{x^2} - 1}}\) liên tục.
Chứng tỏ rằng phương trình \(2{x^5} + a\left( {{x^2} - 1} \right) + 1 = 0\) luôn có nghiệm với mọi số thực \(a\).
Cho hàm số \(g(x)\) liên tục trên \(\mathbb{R}\) trừ điểm \(x = 0\). Xét tính liên tục của hàm số \(f(x) = \frac{{g(x)}}{x}\) tại \(x = 1\).
Cho hàm số \[f(x) = \left\{ {\begin{array}{*{20}{l}}3&{{\rm{ n\~O u }}x \le 1}\\{ax + b}&{{\rm{ n\~O u }}1 < x < 2.{\rm{ }}}\\5&{{\rm{ n\~O u }}x \ge 2}\end{array}} \right.\]Xác định\({\rm{ }}a,b{\rm{ }}\)để hàm số liên tục trên \(\mathbb{R}\).
Chứng minh rằng phương trình \[4{x^4} + 2{x^2} - x - 3 = 0\]có ít nhất 2 nghiệm trong khoảng \[\left( { - 1;1} \right)\].







