Đề kiểm tra Hai mặt phẳng song song (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho hình lăng trụ ABCD.A'B'C'D'. Tìm mệnh đề sai trong các mệnh đề sau
\({\rm{mp}}\left( {AA'B'B} \right)\)song song với \({\rm{mp}}\left( {CC'D'D} \right)\).
Diện tích hai mặt bên bất ki bằng nhau.
\[AA'\] song song với \[CC'\].
Hai mặt phẳng đáy song song với nhau.
Trong các mệnh đề sau. Mệnh đề sai là
Hai mặt phẳng song song thì không có điểm chung.
Hai mặt phẳng cùng song song với một mặt phẳng thì song song với nhau.
Hai mặt phẳng song song với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều song song với mặt phẳng kia.
Một mặt phẳng cắt hai mặt phẳng song song cho trước theo hai giao tuyến thì hai giao tuyến song song với nhau.
Trong không gian cho 2 mặt phẳng (P) và (Q) song song với nhau. Khẳng định nào sau đây sai?
\(d \subset (P)\)và \(d' \subset (Q)\)thì d // d’.
Mọi đường thẳng đi qua điểm \(A \in (P)\) và song song với (Q) đều nằm trong (Q).
Nếu đường thẳng a nằm trong (Q) thì a // (P).
Nếu đường thẳng \(\Delta \) cắt (P) thì \(\Delta \) cắt (Q).
Cho đường thẳng \(a \subset \left( \alpha \right)\) và đường thẳng \(b \subset \left( \beta \right)\). Mệnh đề nào sau đây đúng?
\(\left( \alpha \right)//\left( \beta \right) \Rightarrow a//\left( \beta \right)\)và \(b//\left( \alpha \right).\)
\(a//b \Rightarrow \left( \alpha \right)//\left( \beta \right).\)
a và b chéo nhau.
\(\left( \alpha \right)//\left( \beta \right) \Rightarrow a//b.\)
Cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sau đây sai?
\(\left( {ACD'} \right){\rm{ // }}\left( {A'C'B} \right)\).
\(\left( {ABB'A'} \right){\rm{ // }}\left( {CDD'C'} \right)\).
\(\left( {BDA'} \right){\rm{ // }}\left( {D'B'C} \right)\).
\(\left( {BA'D'} \right){\rm{ // }}\left( {ADC} \right)\).
Cho hình hộp ABCD.A'B'C'D'. Mặt phẳng \[\left( {AB'D'} \right)\] song song với mặt phẳng nào trong các mặt phẳng sau đây?
\[\left( {BCA'} \right)\].
\[\left( {BC'D} \right)\].
\[\left( {A'C'C} \right)\].
\[\left( {BDA'} \right)\].
Cho hình hộp ABCD.A'B'C'D' có các cạnh bên\[AA',BB',CC',DD'\]. Khẳng định nào sai?
\[BB'DC\] là một tứ giác đều.
\[\left( {BA'D'} \right)\] và \[\left( {ADC'} \right)\] cắt nhau.
\[A'B'CD\] là hình bình hành.
\[\left( {AA'B'B} \right){\rm{//}}\left( {DD'C'C} \right)\].
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(I\), \(J\), \(K\) lần lượt là trọng tâm tam giác \(ABC\), \(ACC'\), \(AB'C'\). Mặt phẳng nào sau đây song song với \(\left( {IJK} \right)\)?
\(\left( {BC'{\rm{A}}} \right)\).
\(\left( {AA'B} \right)\).
\(\left( {BB'C} \right)\).
\(\left( {CC'A} \right)\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành tâm \[O\]. Gọi \[M\], \[N\], \(P\) theo thứ tự là trung điểm của \[SA\], \[SD\]và \[AB\]. Khẳng định nào sau đây đúng?
\(\left( {NMP} \right)\;{\rm{//}}\;\left( {SBD} \right)\).
\(\left( {NOM} \right)\) cắt \[\left( {OPM} \right)\].
\[\left( {MON} \right)\;{\rm{//}}\;\left( {SBC} \right)\].
\(\left( {PON} \right) \cap \left( {MNP} \right) = NP\).
Cho hình chóp \(S.ABCD\), có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(M,N\) lần lượt là trung điểm \(SA,SD\). Mặt phẳng \(\left( {OMN} \right)\) song song với mặt phẳng nào sau đây?
\(\left( {SBC} \right)\).
\(\left( {SCD} \right)\).
\(\left( {ABCD} \right)\).
\(\left( {SAB} \right)\).
Cho hình lập phương \(ABCD.A'B'C'D'\). Mặt phẳng \(\left( P \right)\) chứa \(BD\) và song song với mặt phẳng \(\left( {AB'D'} \right)\)cắt hình lập phương theo thiết diện là.
Một tam giác đều.
Một tam giác thường.
Một hình chữ nhật.
Một hình bình hành.
Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh \[a\]. Mặt phẳng \[\left( \alpha \right)\] qua \[AC\] và song song với \[BB'\]. Tính chu vi thiết diện của hình lập phương \[ABCD.A'B'C'D'\] khi cắt bởi mặt phẳng \[\left( \alpha \right)\].
\[2\left( {1 + \sqrt 2 } \right)a\].
\[{a^3}\].
\[{a^2}\sqrt 2 \].
\[\left( {1 + \sqrt 2 } \right)a\]
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho biết tính đúng sai của mỗi phát biểu sau:
a) Hai mặt phẳng phân biệt không cắt nhau thì song song.
b) Nếu mặt phẳng này chứa hai đường thẳng cùng song song với mặt phẳng kia thì hai mặt phẳng đó song song với nhau.
c) Hai mặt phẳng cùng song song với mặt phẳng thứ ba thì song song với nhau.
d) Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành tâm \(O\). Gọi \(M,N\) lần lượt là trung điểm của \(SA\) và \(SD\). Khi đó:
a) \(MN//(SBC)\)
b) \((OMN)//(SBC)\).
c) Gọi \(E\) là trung điểm đoạn \(AB\) và \(F\) là một điểm thuộc đoạn \(ON\). Khi đó \(EF\) cắt với mặt phẳng \((SBC)\).
d) Gọi \(G\) là một điểm trên mặt phẳng \((ABCD)\) cách đều \(AB\) và \(CD\). Khi đó \(GN\)cắt \((SAB)\)
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Gọi \({G_1},{G_2}\) là trọng tâm của các tam giác \({A^\prime }BD,{B^\prime }{D^\prime }C\).
Khi đó:
a) \({A^\prime }{D^\prime }CB\) là hình bình hành
b)\(\left( {{A^\prime }BD} \right)//\left( {{B^\prime }{D^\prime }C} \right)\)
c) \({G_1},{G_2}\) cùng thuộc \(A{C^\prime }\)
d) \({G_1}{G_2} = \frac{2}{3}A{C^\prime }\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(M,N\) lần lượt là trung điểm của \(SA\) và \(SD\). Khi đó:
a) \(ON\) chéo nhau với \(SB\)
b) \((OMN)//(SBC)\).
c) Gọi \(P\) và \(Q\) là trung điểm của \(AB\) và \(ON\). Khi đó\(PQ\) cắt \((SBC)\)
d) Gọi \(R\) là trung điểm \(AD\). Khi đó \((MOR)//(SCD)\).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang có \(AD//BC\), \(AD = 2BC\). Gọi \(E\) là trung điểm của \(AD,O\) là giao điểm của \(AC\) và \(BE,I\) là điểm nằm trên đoạn \(OC\). Mặt phẳng \((P)\) qua \(I\) và song song với \((SBE)\). Tìm các giao tuyến của các mặt của hình chóp với mặt phẳng \((P)\).
Trong không gian, cho bốn điểm \(A,B,C,D\) không đồng phẳng. Qua điểm \(A\) vẽ hai đường thẳng \(m,n\) lần lượt song song với hai đường thẳng \(BC,BD\). Chứng minh rằng \(mp(m,n)\) song song với mặt phẳng \((BCD)\).
Cho hình chóp \(S.ABCD\), gọi \(E\), \(F\) lần lượt là các điểm thuộc các cạnh \(AB,CD\,\). \(M,N,P,Q\) lần lượt là trung điểm của các cạnh \(SA,SB,SC,SD\). Hãy xác định giao tuyến của mặt phẳng \[\left( {EMQ} \right)\]và mặt phẳng \((ABCD)\).
Cho hình lăng trụ tứ giác \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Một mặt phẳng song song với mặt phẳng \(\left( {{A^\prime }{B^\prime }{C^\prime }{D^\prime }} \right)\) cắt các cạnh bên của hình lăng trụ lần lượt tại \({A^{\prime \prime }},{B^{\prime \prime }},{C^{\prime \prime }},{D^{\prime \prime }}\). Hỏi hình tạo bởi các điểm \(A,B,C,D,{A^{\prime \prime }},{B^{\prime \prime }},{C^{\prime \prime }},{D^{\prime \prime }}\) là hình gì?
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Một mặt phẳng song song với mặt bên \(\left( {AB{B^\prime }{A^\prime }} \right)\) của hình hộp và cắt các cạnh \(AD,BC,{A^\prime }{D^\prime },{B^\prime }{C^\prime }\) lần lượt tại \(M,N,{M^\prime },{N^\prime }(H.4.54)\).
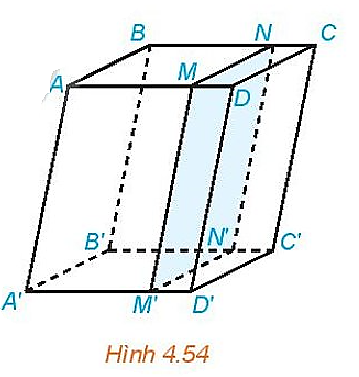
Chứng minh rằng \(ABNM.{A^\prime }{B^\prime }{N^\prime }{M^\prime }\) là hình hộp.
Để xác định mực nước trong một chiếc bể có dạng hình hộp, bác Hà đặt một thanh gỗ đủ dài vào trong bể sao cho một đầu của thanh gỗ dựa vào mép của nắp bể, đầu còn lại nằm trên đáy bể (H.4.53).
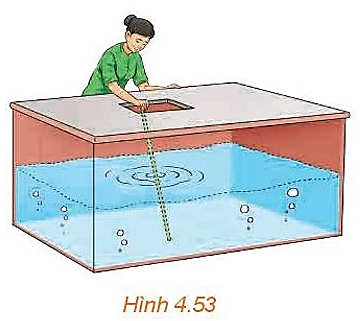
Sau đó bác Hà rút thanh gỗ ra ngoài và tính tỉ lệ giữa độ dài của phần thanh gỗ bị ngâm trong nước và độ dài của cả thanh gỗ. Tỉ lệ này chính bằng tỉ lệ giữa mực nước và chiều cao của bể. Hãy giải thích vì sao.






