35 CÂU HỎI
Cho các số dương \[a \ne 1\]và các số thực \[\alpha \], \[\beta \]. Đẳng thức nào sau đây đúng?
A.\[{a^\alpha } \cdot {a^\beta } = {a^{\alpha + \beta }}\].
B.\[{a^\alpha } \cdot {a^\beta } = {a^{\alpha \beta }}\].
C.\[\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\beta - \alpha }}\].
D.\[{\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha + \beta }}\].
Cho $x$, $y$là hai số thực dương khác \[1\] và $m$, $n$là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
A. $\frac{{{x^m}}}{{{y^n}}} = {\left( {\frac{x}{y}} \right)^{m - n}}$.
B. ${x^m} \cdot {x^n} = {x^{m + n}}$.
C. ${\left( {xy} \right)^n} = {x^n} \cdot {y^n}$.
D. ${\left( {{x^n}} \right)^m} = {x^{n \cdot m}}$.
Cho \[a\]là một số dương, biểu thức ${a^{\frac{2}{3}}}\sqrt a $viết dưới dạng lũy thừa với số mũ hữu tỉ là
A. ${a^{\frac{5}{6}}}$.
B. ${a^{\frac{7}{6}}}$.
C. ${a^{\frac{4}{3}}}$.
D. ${a^{\frac{6}{7}}}$.
Chị Hà gửi vào ngân hàng $20\,\,000\,\,000$đồng với lãi suất \[0,5\% \]/tháng (sau mỗi tháng tiền lãi được nhập vào tiền gốc để tính lãi tháng sau). Hỏi sau \[1\] năm chị Hà nhận được bao nhiêu tiền, biết trong \[1\]năm đó chị Hà không rút tiền lần nào và lãi suất không thay đổi (làm tròn đến hàng nghìn).
A. $21\,\,233\,\,000$đồng.
B. $21\,\,235\,\,000$đồng.
C. $21\,\,234\,\,000$đồng.
D. $21\,\,200\,\,000$đồng.
Cho $0 < a \ne 1,\,M > 0$ và $\alpha $ là số thực tùy ý. Mệnh đề nào sau đây là sai?
A.${\log _a}1 = 0$.
B. ${\log _a}a = 1$.
C. ${\log _a}{a^\alpha } = \alpha $.
D. ${a^{{{\log }_a}M}} = {a^M}$.
Cho $a > 0$; $a \ne 1$và $x$, $y$là hai số thực dương. Phát biểu nào sau đây đúng?
A.${\log _a}\left( {x + y} \right) = {\log _a}x + {\log _a}y$.
B. ${\log _a}\left( {xy} \right) = {\log _a}x + {\log _a}y$.
C. ${\log _a}\left( {xy} \right) = {\log _a}x \cdot {\log _a}y$.
D. ${\log _a}\left( {x + y} \right) = {\log _a}x \cdot {\log _a}y$.
Cho $0 < a \ne 1$. Giá trị của biểu thức $P = {\log _a}\left( {a \cdot \sqrt[3]{{{a^2}}}} \right)$là
A. $\frac{4}{3}$.
B. $3$.
C. $\frac{5}{3}$.
D. $\frac{5}{2}$.
Cho \[a > 0\], \[b > 0\]và \[{a^2} + {b^2} = 7ab\]. Đẳng thức nào dưới đây là đúng?
A. \[{\log _7}\frac{{a + b}}{2} = \frac{1}{3}\left( {{{\log }_7}a + {{\log }_7}b} \right)\].
B. \[{\log _3}\frac{{a + b}}{7} = \frac{1}{2}\left( {{{\log }_3}a + {{\log }_3}b} \right)\].
C. \[{\log _3}\frac{{a + b}}{2} = \frac{1}{7}\left( {{{\log }_3}a + {{\log }_3}b} \right)\].
D. \[{\log _7}\frac{{a + b}}{3} = \frac{1}{2}\left( {{{\log }_7}a + {{\log }_7}b} \right)\].
Trong các hàm số sau đây hàm số nào không phải là hàm số mũ?
A. $y = {5^{\frac{x}{3}}}.$
B. $y = {\left( {\sqrt 3 } \right)^x}.$
C. $y = {4^{ - x}}.$
D. $y = {x^{ - 4}}.$
Cho các hàm số sau:
$y = {\log _2}x$, $y = {\log _{\sqrt 3 }}x$, $y = \ln x$, $y = {\log _{{2^{ - 3}}}}x$, $y = {\log _x}5$.
Có bao nhiêu hàm số lôgarit trong các hàm số trên?
A. $5.$
B. $4.$
C. $3.$
D. $2.$
Tìm mệnh đề đúng trong các mệnh đề sau:
A.$y = {a^x}$ với $a > 1$ là hàm số nghịch biến trên $\left( { - \infty \,;\, + \infty } \right)$.
B. Đồ thị các hàm số $y = {a^x}$ và $y = {\left( {\frac{1}{a}} \right)^x}$với $0 < a$, $a \ne 1$ đối xứng với nhau qua trục $Oy$.
C. Đồ thị hàm số $y = {a^x}$ với $0 < a$, $a \ne 1$ luôn đi qua điểm $\left( {a\,;\,1} \right)$.
D.$y = {a^x}$ với $0 < a < 1$ là hàm số đồng biến trên $\left( { - \infty \,;\, + \infty } \right)$.
Tập xác định của hàm số $y = {\log _3}\left( {{x^2} + 3x + 2} \right)$ là
A. $D = \left[ { - 2; - 1} \right]$.
B. $D = \left( { - \infty ; - 2} \right) \cup \left( { - 1; + \infty } \right)$.
C. $D = \left( { - 2; - 1} \right)$.
D. $D = \left( { - \infty ; - 2} \right] \cup \left[ { - 1; + \infty } \right)$.
Trong các phương trình sau, phương trình nào là phương trình mũ?
A. ${2^x} = 3$.
B. ${\log _3}x = 5$.
C. $\ln x = 4$.
D. $3x - 1 = 0$.
Điều kiện xác định của bất phương trình ${\log _3}\left( {2x - 3} \right) > 1$ là
A.$x > 3$.
B.$x > \frac{3}{2}$.
C.$x \geqslant \frac{3}{2}$.
D.$\frac{3}{2} < x < 3$.
Tập nghiệm của bất phương trình \[{\log _2}x < 1\] là
A. \[\left( {2\,;\, + \infty } \right)\].
B. \[\left( {0\,;\,2} \right)\].
C. \[\left( {0;\,2} \right]\].
D. \[\left( { - \infty \,;\,2} \right)\].
Giải phương trình ${\pi ^{x - 4}} = \frac{1}{\pi }$.
A. $x = 5$.
B. $x = 3$.
C. $x = 4 - \pi $.
D. $x = - 5$
Góc giữa hai đường thẳng bất kì trong không gian là góc giữa
A. Hai đường thẳng cắt nhau và không song song với chúng.
B. Hai đường thẳng lần lượt vuông góc với chúng.
C. Hai đường thẳng cùng đi qua một điểm và lần lượt song song với chúng.
D. Hai đường thẳng cắt nhau và lần lượt vuông góc với chúng.
Khẳng định nào sau đây đúng?
A. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
C. Hai đường thẳng cùng song song với đường thẳng thứ ba thì có thể song song với nhau.
D. Hai đường thẳng cùng song song với đường thẳng thứ ba thì vuông góc với nhau.
Cho hình lập phương $ABCD.A'B'C'D'$. Góc giữa hai đường thẳng $AB$ và $A'C'$ bằng
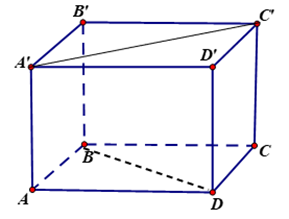
A. $60^\circ .$
B. $30^\circ .$
C. $45^\circ .$
D. $90^\circ .$
Trong không gian cho điểm $A$ và mặt phẳng $\left( P \right)$. Mệnh đề nào dưới đây đúng?
A. Có đúng hai đường thẳng đi qua $A$ và vuông góc với $\left( P \right)$.
B. Có vô số đường thẳng đi qua $A$ và vuông góc với $\left( P \right)$.
C. Không tồn tại đường thẳng đi qua $A$ và vuông góc với $\left( P \right)$.
D. Có đúng một đường thẳng đi qua $A$ và vuông góc với $\left( P \right)$.
Chọn mệnh đề đúng trong các mệnh đề sau?
A.Phép chiếu vuông góc lên mặt phẳng $\left( P \right)$ theo phương $\Delta $ song song với $\left( P \right)$ được gọi là phép chiếu vuông góc lên mặt phẳng $\left( P \right)$.
B. Phép chiếu song song lên mặt phẳng $\left( P \right)$ theo phương $\Delta $ được gọi là phép chiếu vuông góc lên mặt phẳng $\left( P \right)$.
C. Phép chiếu vuông góc lên mặt phẳng $\left( P \right)$ theo phương $\Delta $ được gọi là phép chiếu vuông góc lên mặt phẳng $\left( P \right)$.
D. Phép chiếu song song lên mặt phẳng $\left( P \right)$ theo phương $\Delta $ vuông góc với $\left( P \right)$ được gọi là phép chiếu vuông góc lên mặt phẳng $\left( P \right)$.
Cho hình chóp \[S.ABC\]có \[SA \bot \left( {ABC} \right)\]và tam giác \[ABC\]vuông tại \[B\]. Gọi \[AH\]là đường cao của tam giác \[SAB\]. Tìm mệnh đề sai?
A. \[SA \bot BC\].
B. \[AB \bot SC\].
C. \[AH \bot SC\].
D. \[AH \bot BC\].
Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$. Hãy chọn khẳng định đúng?
A. Hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ được gọi là vuông góc với nhau nếu góc giữa chúng bằng $180^\circ $.
B. Hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ được gọi là vuông góc với nhau nếu góc giữa chúng bằng $60^\circ $.
C. Hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ được gọi là vuông góc với nhau nếu góc giữa chúng bằng $90^\circ $.
D. Hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ được gọi là vuông góc với nhau nếu góc giữa chúng bằng $30^\circ $.
Trong lăng trụ đều, khẳng định nào sau đây sai?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình bình hành.
Cho hình chóp $S.ABCD$có đáy $ABCD$là hình thoi, $SA = SC$. Khẳng định nào sau đây đúng?
A. Mặt phẳng \[\left( {SBD} \right)\]vuông góc với mặt phẳng $\left( {ABCD} \right)$.
B. Mặt phẳng $\left( {SBC} \right)$vuông góc với mặt phẳng $\left( {ABCD} \right)$.
C. Mặt phẳng $\left( {SAD} \right)$vuông góc với mặt phẳng $\left( {ABCD} \right)$.
D. Mặt phẳng $\left( {SAB} \right)$vuông góc với mặt phẳng $\left( {ABCD} \right)$.
Cho hai đường thẳng \[{d_1}\] và ${d_2}$ chéo nhau. Mệnh đề nào sau đây đúng?
B. Khoảng cách giữa \[{d_1}\] và ${d_2}$ bằng khoảng cách từ điểm $B$ trên ${d_2}$ đến ${d_1}.$
C. Khoảng cách giữa \[{d_1}\] và ${d_2}$ là độ dài của đoạn $AB$ với $AB$ vuông góc với \[{d_1}\] và ${d_2}$.
D. Khoảng cách giữa \[{d_1}\] và ${d_2}$ bằng khoảng cách từ điểm $A$ trên ${d_1}$ đến mặt phẳng $\left( P \right)$ chứa ${d_2}$ và song song với ${d_1}.$
Mệnh đề nào sau đây đúng?
A. Khoảng cách từ một điểm \[A\] bất kì đến mặt phẳng $\left( P \right)$ bằng độ dài đoạn $AH$ với $H$ là một điểm bất kì trên mặt phẳng $\left( P \right).$
B. Khoảng cách từ một điểm $A$ bất kì đến mặt phẳng $\left( P \right)$ bằng độ dài đoạn $AH$ với $AH \bot \left( P \right).$
C. Khoảng cách từ một điểm $A$ bất kì đến mặt phẳng $\left( P \right)$ là độ dài nhỏ nhất của đoạn $AH.$
D. Khoảng cách từ một điểm $A$ bất kì đến mặt phẳng $\left( P \right)$ bằng độ dài đoạn $AH$ với $H$ là hình chiếu vuông góc của $A$ trên $\left( P \right).$
Cho khối chóp \[S.ABC\] có \[\left( {SAB} \right) \bot \left( {ABC} \right),\left( {SAC} \right) \bot \left( {ABC} \right)\], \[SA = a,\]\[AB = AC = 2a,\]\[BC = 2a\sqrt 2 \]. Gọi $M,I$lần lượt là trung điểm của $BC,AB.$Khoảng cách từ điểm $A$ đến mặt phẳng \[\left( {SMI} \right)\] là
A. \[a.\]
B. \[\frac{a}{{\sqrt 2 }}.\]
C. \[a\sqrt 2 .\]
D. \[2a.\]
Cho hình chóp\[S.ABC\] có đáy là tam giác đều. Hình chiếu vuông góc của $S$ lên mặt phẳng \[\left( {ABC} \right)\] trùng với trung điểm $H$ của cạnh $BC$. Biết tam giác $SBC$ là tam giác đều. Xác định góc giữa $SA$ và \[\left( {ABC} \right).\]
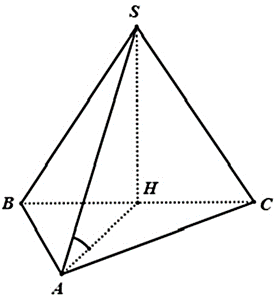
A. \[\widehat {SHB}.\]
B.\[\widehat {SHA}.\]
C. \[\widehat {SAH}.\]
D. \[\widehat {ASH}.\]
Cho hình chóp \[S.ABCD\] có \[SA \bot \left( {ABCD} \right)\] đáy \[ABCD\] là hình thoi. Góc \[BAC\] là một góc phẳng của góc nhị diện nào sau đây?
A.\[\left[ {B\,,\,SA\,,\,D} \right]\].
B. \[\left[ {B\,,\,SA\,,\,C} \right]\].
C.\[\left[ {D\,,\,SA\,,\,C} \right]\].
D.\[\left[ {B,\,SA\,,\,D} \right]\].
Cho hình lập phương \[ABCD.A'B'C'D'\]cạnh $a$. Gọi \[\alpha \]là góc giữa \[AC\] và mặt phẳng \[\left( {A'BCD'} \right).\] Chọn khẳng định đúng trong các khẳng định sau.
A. \[\alpha = 30^\circ .\]
B. \[\alpha = 45^\circ .\]
C. \[\tan \alpha = \frac{2}{{\sqrt 3 }}.\]
D. \[\tan \alpha = \sqrt 2 .\]
Cho hình chóp tứ giác đều $S.ABCD$. Cắt hình chóp bởi mặt phẳng song song với đáy và cắt tất cả các cạnh bên của hình chóp thì ta được
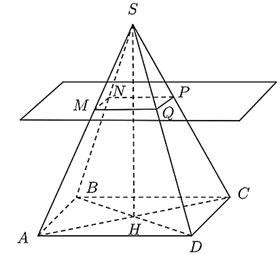
A. hình chóp cụt tứ giác đều.
B. hình chóp cụt tam giác đều.
C. hình lăng trụ tứ giác đều.
D. hình lăng trụ tứ giác đều.
Cho khối chóp có diện tích đáy $B$ và chiều cao $h$. Thể tích $V$ của khối chóp đã cho được tính theo công thức nào dưới đây?
A. $V = \frac{1}{3}Bh$.
B. $V = \frac{4}{3}Bh$.
C.$V = 6Bh$.
D.$V = Bh$.
Thể tích $V$ của khối hộp chữ nhật có các kích thước \[5;\,\,6;\,\,7\]bằng:
A. $V = 210$.
B. $V = 18$.
C.$V = 77$.
D.$V = 12$.
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác đều cạnh $a$, biết \[SA \bot \left( {ABC} \right)\] và $SA = 3a\sqrt 3 $. Tính theo $a$ thể tích khối chóp \[S.ABC\].
A. $\frac{a}{4}$.
B. $\frac{{{a^3}}}{2}$.
C. $\frac{{{a^3}}}{4}$.
D. $\frac{{3{a^3}}}{4}$.

