35 CÂU HỎI
Đổi từ rađian sang độ với số đo $ - \frac{{13\pi }}{5}$ ta được
A. $36^\circ $.
B. $468^\circ $.
C. $ - 468^\circ .$
D. $486^\circ $.
Điểm $M$ trên đường tròn lượng giác dưới đây biểu diễn cho góc lượng giác nào trong các đáp án A, B, C, D?
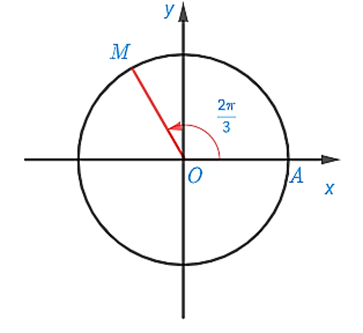
A.$\frac{{2\pi }}{3} + k\pi ,k \in \mathbb{Z}$.
B.$\frac{{2\pi }}{3}$.
C.$ - \frac{{2\pi }}{3}$.
D.$ - \frac{{5\pi }}{3}$
Chọn khẳng định đúng.
A.$\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 - \tan a\tan b}}$.
B.$\tan \left( {a - b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}$.
C.$\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}$.
D.$\tan \left( {a + b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}$.
Giả sử các đẳng thức đều có nghĩa. Đẳng thức sai trong các đẳng thức sau là
A.$1 + \sin 2a = {\left( {\sin a + \cos a} \right)^2}$.
B.$\tan 2a = \frac{{2{{\tan }^2}a}}{{1 - \tan a}}$.
C.$1 - \cos 2a = 2{\sin ^2}a$.
D.$\sin a + \cos a = \sqrt 2 \sin \left( {a + \frac{\pi }{4}} \right)$.
Khẳng định nào dưới đây là sai?
A. Hàm số $y = \cos x$ có tập xác định là $\mathbb{R}$.
B. Hàm số $y = \cos x$ có tập giá trị là $\left[ { - 1;\,1} \right]$.
C. Hàm số $y = \cos x$ là hàm số lẻ.
D. Hàm số $y = \cos x$ tuần hoàn với chu kì $2\pi $.
Tập xác định của hàm số $\frac{{\cos x}}{{{{\sin }^2}x}}$ là
A. $D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}$.
B. $D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}$.
C. $D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}$.
D. $D = \mathbb{R}\backslash \left\{ { - \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}$.
Hàm số $y = A\sin \omega t$$\left( {\omega \ne 0} \right)$ là hàm số tuần hoàn với chu kì
A. $T = \frac{{2\pi }}{\omega }$.
B. $T = \frac{{2\pi }}{{\left| \omega \right|}}$.
C. $T = 2\pi $.
D. $T = - \frac{{2\pi }}{{\left| \omega \right|}}$.
Phép biến đổi nào trong các phép biến đổi sau đây không phải là phép biến đổi tương đương?
A. Cộng hai vế của một phương trình với cùng một số thực dương.
B. Trừ hai vế của một phương trình với cùng một số thực âm.
C. Nhân hai vế của một phương trình với cùng một số thực âm.
D. Bỏ mẫu của phương trình chứa ẩn dưới mẫu.
Khẳng định nào sau đây là đúng?
A. $\cos u = \cos v \Leftrightarrow \left[ \begin{gathered}
u = v + k2\pi \hfill \\
u = \pi - v + k2\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.
B. $\cos u = \cos v \Leftrightarrow \left[ \begin{gathered}
u = v + k2\pi \hfill \\
u = - v + k2\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.
C. $\cos u = \cos v \Leftrightarrow \left[ \begin{gathered}
u = v + k\pi \hfill \\
u = \pi - v + k\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.
D. $\cos u = \cos v \Leftrightarrow \left[ \begin{gathered}
u = v + k\pi \hfill \\
u = - v + k\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.
Tất cả các nghiệm của phương trình $\sin x = 1$ là
A.\[x = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\].
B.\[x = - \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\].
C.\[x = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\].
D.\[x = \pi + k2\pi \left( {k \in \mathbb{Z}} \right)\].
Khẳng định nào sau đây là sai?
A. Một dãy số tăng thì bị chặn dưới.
B. Một dãy số giảm thì bị chặn trên.
C. Một dãy số bị chặn thì phải tăng hoặc giảm.
D. Một dãy số không đổi thì bị chặn.
Cho dãy số $\left( {{u_n}} \right)$ có ${u_n} = {\left( { - 1} \right)^n}$. Chọn khẳng định đúng nhất trong các khẳng định dưới đây.
A.$\left( {{u_n}} \right)$ là dãy số bị chặn.
B. $\left( {{u_n}} \right)$ là dãy số không bị chặn.
C. $\left( {{u_n}} \right)$ là dãy số bị chặn trên.
D. $\left( {{u_n}} \right)$ là dãy số bị chặn dưới.
Dãy số này dưới đây là một cấp số cộng?
A.$1;\, - 3;\, - 7;\, - 11;\, - 15;...$.
B.$1;\, - 3;\, - 6;\, - 9; - 12;...$.
C.$1;\, - 2;\, - 4;\, - 6;\, - 8;...$.
D.$1;\, - 3;\, - 5; - 7; - 9;...$.
Cho cấp số cộng $\left( {{u_n}} \right)$ có số hạng đầu ${u_1} = - \frac{1}{2}$ và công sai $d = \frac{1}{2}$. Năm số hạng đầu liên tiếp của cấp số cộng này là
A.$ - \frac{1}{2};\,\,\,0;\,\,\,1;\,\,\,\frac{1}{2};\,\,\,1$.
B.$ - \frac{1}{2};\,\,\,0;\,\,\,\frac{1}{2};\,\,\,0;\,\,\,\frac{1}{2}$.
C.$\frac{1}{2};\,\,\,0;\,\,\,1;\,\,\,\frac{1}{2};\,\,\,1$.
D.$ - \frac{1}{2};\,\,\,0;\,\,\,\frac{1}{2};\,\,\,1;\,\,\,\frac{3}{2}$.
Trong các dãy số sau đây, dãy số nào là cấp số nhân.
A.$ - \frac{1}{2};\,\,\,0;\,\,\,1;\,\,\,\frac{1}{2};\,\,\,1$.
B.$ - 1;\,\, - 3;\,\,1;\,\,3;\,\,5$.
C.$1;\,\,2;\,\,4;\,\,16;\,\,256$.
D.$1;\,\,2;\,\,4;\,\,8;\,\,16$.
Cho dãy số $\left( {{u_n}} \right)$ với \[{u_n} = \frac{3}{2}{.5^n}\]. Khẳng định nào sau đây là đúng?
A.$\left( {{u_n}} \right)$ không phải là cấp số nhân.
B. $\left( {{u_n}} \right)$ là cấp số nhân có công bội $q = 5$ và số hạng đầu ${u_1} = \frac{3}{2}$.
C. $\left( {{u_n}} \right)$ là cấp số nhân có công bội $q = 5$ và số hạng đầu ${u_1} = \frac{{15}}{2}$.
D. $\left( {{u_n}} \right)$ là cấp số nhân có công bội $q = 5$ và số hạng đầu ${u_1} = 3$.
Cho mẫu số liệu ghép nhóm sau:
|
Nhóm |
$\left[ {0;2} \right)$ |
$\left[ {2;4} \right)$ |
$\left[ {4;6} \right)$ |
$\left[ {6;8} \right)$ |
$\left[ {8;10} \right)$ |
$\left[ {10;12} \right)$ |
$\left[ {12;14} \right)$ |
|
Tần số |
5 |
10 |
40 |
20 |
16 |
3 |
6 |
Mệnh đề nào dưới đây là đúng?
A. Giá trị 4 thuộc vào nhóm $\left[ {2;4} \right)$.
B. Tần số của nhóm $\left[ {8;10} \right)$ là 20.
C. Tần số của nhóm $\left[ {4;6} \right)$ là 40.
D. Giá trị 3 thuộc vào nhóm $\left[ {10;12} \right)$.
Mẫu số liệu sau đây cho biết cân nặng của 20 con mèo vừa chào đời.
|
Cân nặng (gam) |
$\left[ {90;95} \right)$ |
$\left[ {95;100} \right)$ |
$\left[ {100;105} \right)$ |
$\left[ {105;110} \right)$ |
$\left[ {110;\,115} \right)$ |
|
Số lượng |
3 |
3 |
6 |
6 |
2 |
Hãy cho biết có bao nhiêu con mèo có cân nặng nhỏ hơn 100 gam trong mẫu số liệu trên.
A. 12.
B. 6.
C. 9.
D. 10.
Mẫu số liệu ở Câu 18 có số mốt là
A. 1.
B. 2.
C. $\left[ {100;105} \right)$.
D. $\left[ {105;110} \right)$.
Nhóm chứa trung vị trong mẫu số liệu ở Câu 18 là
A. $\left[ {90;95} \right)$.
B. $\left[ {95;100} \right)$.
C. $\left[ {100;105} \right)$.
D. $\left[ {105;110} \right)$.
Cho \[\tan \alpha = - \frac{4}{5}\]với \[\frac{{{\text{3}}\pi }}{{\text{2}}} < \alpha < 2\pi \]. Khi đó
A. \[\sin \alpha = - \frac{4}{{\sqrt {41} }}\], \[\cos \alpha = - \frac{5}{{\sqrt {41} }}\].
B.\[\sin \alpha = \frac{4}{{\sqrt {41} }}\], \[\cos \alpha = \frac{5}{{\sqrt {41} }}\].
C. \[\sin \alpha = - \frac{4}{{\sqrt {41} }}\]\[\cos \alpha = \frac{5}{{\sqrt {41} }}\].
D.\[\sin \alpha = \frac{4}{{\sqrt {41} }}\], \[\cos \alpha = - \frac{5}{{\sqrt {41} }}\].
Cho hai góc nhọn \[a\] và \[b\] với \[\sin a = \frac{1}{3}\], \[\sin b = \frac{1}{2}\]. Giá trị của \[\sin 2\left( {a + b} \right)\] là
A.\[\frac{{2\sqrt 2 + 7\sqrt 3 }}{{18}}.\]
B.\[\frac{{3\sqrt 2 + 7\sqrt 3 }}{{18}}.\]
C.\[\frac{{4\sqrt 2 + 7\sqrt 3 }}{{18}}.\]
D.\[\frac{{5\sqrt 2 + 7\sqrt 3 }}{{18}}.\]
Biểu thức \[A = \frac{{2{{\cos }^2}2\alpha + \sqrt 3 \sin 4\alpha - 1}}{{2{{\sin }^2}2\alpha + \sqrt 3 \sin 4\alpha - 1}}\] có kết quả rút gọn là
A.\[\frac{{\cos \left( {4\alpha + 30^\circ } \right)}}{{\cos \left( {4\alpha - 30^\circ } \right)}}.\]
B.\[\frac{{\cos \left( {4\alpha - 30^\circ } \right)}}{{\cos \left( {4\alpha + 30^\circ } \right)}}.\]
C.\[\frac{{\sin \left( {4\alpha + 30^\circ } \right)}}{{\sin \left( {4\alpha - 30^\circ } \right)}}.\]
D.\[\frac{{\sin \left( {4\alpha - 30^\circ } \right)}}{{\sin \left( {4\alpha + 30^\circ } \right)}}.\]
Hàm số $y = \sin x$ đồng biến trên khoảng nào dưới đây?
A.$\left( {\frac{{19\pi }}{2};10\pi } \right)$.
B.$\left( { - 6\pi ; - 5\pi } \right)$.
C.$\left( { - \frac{{7\pi }}{2}; - 3\pi } \right)$.
D.$\left( {7\pi ;\frac{{15\pi }}{2}} \right)$.
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 7 - 2\cos \left( {x + \frac{\pi }{4}} \right)$ lần lượt là
A.$\left( {\frac{{19\pi }}{2};10\pi } \right)$.
B.$5;9$.
C.$ - 2;2$.
D.$4;7$.
Giải phương trình $\sin x = - \sin \left( {x - \frac{\pi }{3}} \right)$.
A.$x = \frac{\pi }{3} + k2\pi $$\left( {k \in \mathbb{Z}} \right)$.
B.$x = - \frac{\pi }{3} + k2\pi $$\left( {k \in \mathbb{Z}} \right)$.
C.$x = \frac{\pi }{6} + k\pi $$\left( {k \in \mathbb{Z}} \right)$.
D.$x = - \frac{\pi }{6} + k\pi $$\left( {k \in \mathbb{Z}} \right)$.
Phương trình $\sin x - \sqrt 3 \cos x = 1$ chỉ có các nghiệm là
A.$\left[ \begin{gathered}
x = \frac{\pi }{2} + k2\pi \hfill \\
x = \frac{{7\pi }}{6} + k2\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.
B.$\left[ \begin{gathered}
x = - \frac{\pi }{2} + k2\pi \hfill \\
x = - \frac{{7\pi }}{6} + k2\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.
C.$\left[ \begin{gathered}
x = - \frac{\pi }{2} + k2\pi \hfill \\
x = \frac{{7\pi }}{6} + k2\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.
D.$\left[ \begin{gathered}
x = \frac{\pi }{2} + k2\pi \hfill \\
x = - \frac{{7\pi }}{6} + k2\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.
Cho dãy số $\left( {{u_n}} \right)$ có ${u_n} = \frac{{2n}}{{{n^2} + 1}}$. Số $\frac{9}{{41}}$ là số hạng thứ bao nhiêu của dãy số $\left( {{u_n}} \right)$?
A. 10.
B. 9.
C. 8.
D. 11.
Dãy số nào sau đây là dãy số bị chặn?
A.\[{a_n} = \sqrt {n + 10} \].
B.${b_n} = \sqrt {5n + 10} $.
C.${u_n} = \sqrt {n + 10} + \sqrt {20 - n} $.
D.${v_n} = \sqrt {5n - 6} $.
Cho cấp số cộng $\left( {{u_n}} \right)$ biết ${u_5} = 18$ và $4{S_n} = {S_{2n}}$. Số hạng đầu ${u_1}$ và công sai $d$ là
A.${u_1} = 3;\,\,d = 2$.
B.${u_1} = 2;\,\,d = 2$.
C.${u_1} = 2;\,\,d = 4$.
D.${u_1} = 2;\,\,d = 3$.
Cho cấp số cộng \[\left( {{u_n}} \right)\] biết \[{u_{20}} = - 52\] và \[{u_{51}} = - 145\]. Số hạng tổng quát của cấp số cộng \[\left( {{u_n}} \right)\]là
A.\[{u_n} = - 3n + 8\].
B.\[{u_n} = 5 + 3\left( {n - 1} \right)\].
C. \[{u_n} = 3n - 3\].
D.\[{u_n} = - 3n + 5\].
Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = 24$ và $\frac{{{u_4}}}{{{u_{11}}}} = 16384$. Số hạng ${u_{17}}$ là
A.$\frac{3}{{67108864}}.$
B.$\frac{3}{{368435456}}.$
C.$\frac{3}{{536870912}}.$
D.$\frac{3}{{2147483648}}.$
Tính tổng \[S = 9 + 99 + 999 + ..... + \underbrace {99...9}_{9\,\,{\text{chu}}\,\,{\text{so}}\,9}\] ta được kết quả là
A. 111111110.
B. 111111111.
C. 1111111111.
D. 1111111101.
Người ta tiến hành phỏng vấn 50 người về một mẫu áo phông mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm 100. Kết quả được trình bày trong bảng sau:
|
Nhóm |
$\left[ {50;\,60} \right)$ |
$\left[ {60;\,70} \right)$ |
$\left[ {70;\,80} \right)$ |
$\left[ {80;\,90} \right)$ |
$\left[ {90;\,100} \right)$ |
|
Số lượng |
9 |
10 |
23 |
6 |
2 |
Điểm trung bình của mẫu áo trong mẫu số liệu trên là
A. $74,1$.
B. $74,34$.
C. $71,14$.
D. $71,4$.
Trung vị của mẫu số liệu ghép nhóm trên Câu 34 gần nhất với giá trị nào dưới đây.
A. $72$.
B. $73$.
C. $74$.
D. $75$.

