35 CÂU HỎI
Nguyên hàm của hàm số là:
A.
B.
C.
D.
Tìm một nguyên hàm F(x) của hàm số , biết rằng , , . F(x) là biểu thức nào sau đây
A.
B.
C.
D.
Nguyên hàm của hàm số là :
A.
B.
C.
D. Kết quả khác
Gọi F(x) là một nguyên hàm của hàm số .Hàm số nào sau đây không phải là F(x):
A.
B.
C.
D.
Tính nguyên hàm được kết quả nào sau đây?
A.
B.
C.
D.
Cho . Khi đó bằng
A. 2 .
B. 4 .
C. 6 .
D. 8
Cho hàm số f liên tục trên đoạn có một nguyên hàm là hàm F trên đoạn . Trong các phát biểu sau, phát biểu nào sai ?
A.
B. với mọi
C.
D. Hàm số G cho bởi cũng thỏa mãn
Tích phân bằng
A. I = 1.
B. I = 2.
C. I = 3
D. I = -1.
Tích phân bằng
A.
B.
C.
D.
Biết . Khi đó nhận giá trị bằng:
A. b = 0 hoặc b = 2.
B. b = 0 hoặc b = 4.
C. b= 1 hoặc b= 2.
D. b = 1 hoặc b = 4.
Giả sử hàm số f liên tục trên đoạn thỏa mãn . Giá trị của tích phân là
A. -6 .
B. 6 .
C. -3 .
D. 3.
Tích phân bằng:
A.
B.
C.
D.
Tích phân bằng:
A. 6
B. 5
C. 4
D.
Tích phân bằng:
A. L = p
B. L = -p
C. L = -2
D. L = 0
Để hàm số thỏa mãn và thì a, b nhận giá trị
A.
B.
C.
D.
Tích phân bằng:
A.
B.
C.
D.
Diện tích hình phẳng được giới hạn bởi các đường và đường thẳng là:
A.
B.
C.
D.
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là:
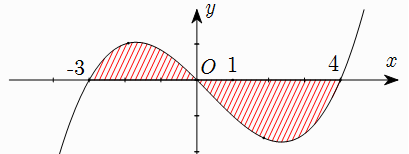
A.
B.
C.
D.
Cho hai hàm số và liên tục trên và thỏa mãn:
. Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng (H) giới hạn bởi các đường: , . Khi đó V dược tính bởi công thức nào sau đây?
A.
B.
C.
D.
Cho hình phẳng giới hạn bởi các đường và quay xung quanh trục Ox. Thể tích của khối tròn xoay được tạo thành bằng:
A.
B.
C.
D.
Biết diện tích của hình phẳng giới hạn bởi các đường và là với a , b , c là các số nguyên. Tính
A. P = -2
B. P = 3
C. P = 0
D. P = 4
Cho parabol và đường thẳng . Biết rằng tồn tại m để diện tích hình phẳng giới hạn bởi (P) và d đạt giá trị nhỏ nhất, tính diện tích nhỏ nhất đó.
A. S = 4
B. S =
C. S = 0
D. S =
Trong không gian Oxyz với hệ tọa độ cho . Tìm tọa độ điểm A
A.
B.
C.
D.
Cho . Tìm m, n sao cho và cùng phương.
A. m = 2 và n = –1.
B. m = –2 và n = 1.
C. m = 1 và n = –2.
D. m = –1 và n = 2.
Cho .
Tìm m để ba vectơ đó đồng phẳng.
A. m = 0 V m = –2.
B. m = –1 V m = 2.
C. m = 0 V m = –1.
D. m = 2 V m = 0.
Trong không gian với hệ tọa độ Oxyz , cho hình bình hành MNPQ có M ( 2; 0; 0) ; N ( 0; -3; 0 ) ; P ( 0; 0; -4). Tìm tọa độ điểm Q
A.
B.
C.
D.
Trong không gian Oxyz, cho điểm . Tọa độ hình chiếu của M trên trục Ox là:
A. (-1;2;0)
B. (-1;0;0)
C.
D. (0;2;0)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(-1; 2; -3), B(1; 0; 2), C(x,y,-2) thẳng hàng. Khi đó tổng x + y bằng bao nhiêu?
A. x + y = 1
B. x + y = 17
C. x + y =
D. x + y =
Trong không gian với hệ tọa độ Oxyz, cho A(-1; 2; 4); B (- 1; 1; 4); C (0; 0; 4). Tìm số đo của
A.
B.
C.
D.
Trong không gian , cho bốn điểm . Tính góc giữa hai đường thẳng AB và CD.
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ , cho ba điểm . Tìm tọa độ điểm M thỏa mãn .
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ , cho tam giác ABC với . Độ dài chiều cao AH của tam giác bằng
A.
B.
C.
D.
Trong không gian với hệ trục toạ độ , cho điểm và mặt cầu . Một đường thẳng d đi qua A, cắt mặt cầu tại hai điểm M, N. Độ dài ngắn nhất của MN là
A. 8
B. 4
C. 6
D. 10
Trong không gian với hệ tọa độ , cho tứ diện ABCD có A(-2;1;1), B(-2;1;1), C(-1;0;0), D(1;1;1). Thể tích V của tứ diện ABCD bằng bao nhiêu?
A. V =
B. V =
C. V = 2
D. V = 1
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.ABCD có S(1;3;-1), A(1;0;0), B(0,-2,0), C(0;0;4) . Độ dài đường cao của hình chóp S.ABCD bằng
A.
B.
C.
D.


