Đề kiểm tra Đường thẳng và mặt phẳng trong không gian (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho bốn điểm A,B,C,D không đồng phẳng. Gọi \[I,K\] lần lượt là trung điểm hai đoạn thẳng \[AD\] và \[BC\]. \[IK\] là giao tuyến của cặp mặt phẳng nào sau đây?
\[\left( {IBC} \right)\] và \[\left( {KBD} \right)\].
\[\left( {IBC} \right)\] và \[\left( {KCD} \right)\].
\[\left( {IBC} \right)\] và \[\left( {KAD} \right)\].
\[\left( {ABI} \right)\] và \[\left( {KAD} \right)\].
Cho hình chóp S.ABCD có ABCD là hình thang. Giao tuyến của 2 mặ t phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) là
\(SI\) với \(I\) là giao điểm của \(AB\) và \(CD\).
\(SI\) với \(I\) là giao điểm của \(AC\) và \(BD\).
\(Sx\) với \(Sx{\rm{//}}AB\).
\(SI\) với \(I\) là giao điểm của \(AD\) và \(BC\).
Cho tứ diện ABCD. Gọi \[G\] là trọng tâm của tam giác \[BCD\]. Giao tuyến của mặt phẳng \[\left( {ACD} \right)\] và \[\left( {GAB} \right)\] là
\[AM\] (\[M\] là trung điểm của \[AB\]).
\[AN\] (\[N\] là trung điểm của \[CD\] ).
\[AH\] (\[H\] là hình chiếu của \[B\] trên \[CD\]).
\[AK\] (\[K\] là hình chiếu của \[C\] trên \[BD\]).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi \[M\] là trung điểm của \[SC.\] Gọi \[I\] là giao điểm của \[AM\] với mặt phẳng \[\left( {SBD} \right).\] Mệnh đề nào dưới đây đúng?
\(\overrightarrow {IA} = - \,2\overrightarrow {IM} \).
\(\overrightarrow {IA} = - \,3\overrightarrow {IM} \).
\(\overrightarrow {IA} = 2\overrightarrow {IM} \).
\(IA = 2,5IM\).
Cho hình chóp S.ABCD như hình vẽ bên. Có ABCD là tứ giác lồi. Với \[{\rm{W}}\] là điểm thuộc vào cạnh \(SD\), \(X\) là giao điểm của hai đường thẳng \(AC\)và \(BD\) và \(Y\) là giao điểm của hai đường thẳng \(SX\) và \(B{\rm{W}}\). Gọi \(P\) là giao điểm của \(DY\)và \(\left( {SAB} \right)\). Khẳng định nào sau đây là khẳng định đúng?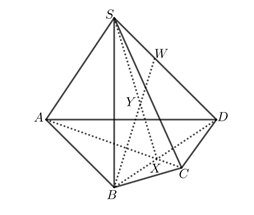
\(P\) là giao điểm của hai đường thẳng \(DY\) với \(SB\).
\(P\) là giao điểm của hai đường thẳng \(DY\) với \(SA\).
\(P\) là giao điểm của hai đường thẳng \(DY\) với \(AB\).
\(P\) là giao điểm của hai đường thẳng \(B{\rm{W}}\) với \(SC\).
Cho bốn điểm \(A\), \(B\), \(C\), \(D\) không đồng phẳng. Gọi \(M\), \(N\) lần lượt là trung điểm của \(AC\) và \(BC\). Trên đoạn \(BD\) lấy điểm \(P\) sao cho \(BP = 2PD\). Giao điểm của đường thẳng \(CD\) và mặt phẳng \(\left( {MNP} \right)\) là giao điểm của
\(CD\)và \(NP\).
\(CD\)và \(MN\).
\(CD\)và \(MP\).
\(CD\)và \(AP\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi \(I\), \(J\) lần lượt là trung điểm \(SB\) và \(SD\). Thiết diện của mặt phẳng \(\left( {AIJ} \right)\) với hình chóp S.ABCD là 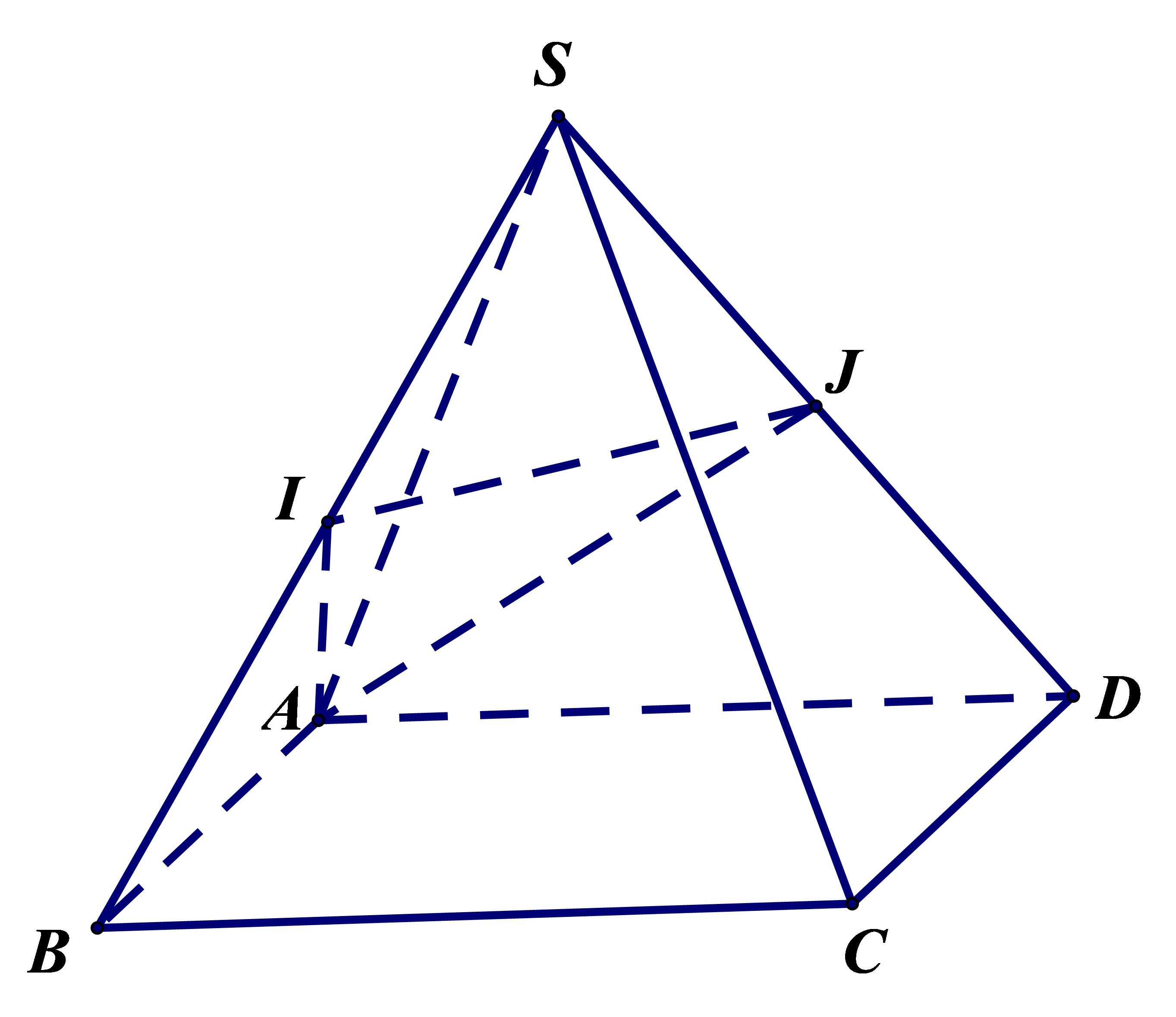
tứ giác.
tam giác.
lục giác.
ngũ giác.
Cho hình chóp S.ABCD đáy là hình bình hành tâm \(O\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(SA,\,\,SC\). Mp \(\left( P \right) = \left( {MNB} \right)\). Gọi \(I = SO \cap \left( P \right),\,\,K = SD \cap \left( P \right),\,\,\)\(E = DA \cap \left( P \right),\,\,\)\(F = DC \cap \left( P \right)\). Khi đó:
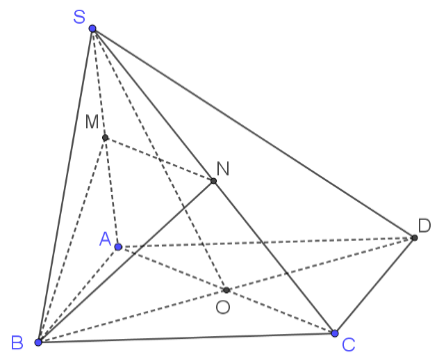
Ba điểm \(E,\,\,B,\,\,K\) thẳng hàng.
Ba điểm \(F,\,\,K,\,\,I\) thẳng hàng.
Ba điểm \(E,\,\,B,\,\,I\) thẳng hàng.
Ba điểm \(E,\,\,B,\,\,F\) thẳng hàng.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi \[M,N\] lần lượt là trung điểm \[AD\] và \[BC\]. Giao tuyến của hai mặt phẳng \[\left( {SMN} \right)\] và \[\left( {SAC} \right)\] là
\[SD\].
\[SO\](\[O\] là tâm hình bình hành \[ABCD\]).
\[SG\] (\[G\] là trung điểm \[AB\]).
\[SF\](\[F\] là trung điểm \[CD\]).
Cho 4 điểm không đồng phẳng \[A,B,C,D\]. Gọi \[I,K\]lần lượt là trung điểm của \[AD\] và \[BC\]. Giao tuyến của hai mặt phẳng \[\left( {IBC} \right)\] và \[\left( {KAD} \right)\]là
\[IK\].
\[BC\].
\[AK\].
\[DK\].
Cho tứ diện ABCD. Lấy điểm \(M\) sao cho \(AM = 2CM\) và \(N\) là trung điểm \(AD\). Gọi \(O\) là một điểm thuộc miền trong của \(\Delta BCD\). Giao điểm của \(BC\) với \(\left( {OMN} \right)\) là giao điểm của \(BC\) với
\(OM\).
\(MN\).
\(A,B\) đều đúng.
\(A,B\) đều sai.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Các điểm \(M,\,N\)thuộc các cạnh \(AB,\,SC\). Phát biểu nào sau đây đúng?
Giao điểm của \(MN\)với \(\left( {SBD} \right)\)là giao điểm của \(MN\)với \(BD\).
Đường thẳng \(MN\)không cắt mặt phẳng \(\left( {SBD} \right)\).
Giao điểm của \(MN\)với \(\left( {SBD} \right)\)là giao điểm của \(MN\)với \(SI\), trong đó \(I\)là giao điểm của \(CM\)với \(BD\).
Giao điểm của \(MN\)với \(\left( {SBD} \right)\)là \(M\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho bốn điểm \(A,B,C,D\) không đồng phẳng. Gọi \(M,N\) lần lượt là trung điểm của \(AC\) và \(BC\). Trên đoạn \(BD\) lấy điểm \(P\) sao cho \(BP = 2PD\), \(E = CD \cap NP\). Khi đó:
a) \(NM\) là giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\),\((ABC)\)
b) \(DC\) là giao tuyến của hai mặt phẳng \(\left( {BCD} \right),(ADC)\)
c) Giao điểm của đường thẳng \(CD\) và mặt phẳng \((MNP)\) là điểm \(E\)
d) Giao điểm của đường thẳng \(AD\) và mặt phẳng \((MNP)\) là giao điểm của đường thẳng \(AD\) với đường thẳng \(MP\)
Cho tứ giác ABCD có \(AC\) và \(BD\) giao nhau tại \(O\) và một điểm \(S\) không thuộc mặt phẳng \((ABCD)\). Trên đoạn \(SC\) lấy một điểm \(M\) không trùng với \(S\) và \(C\),\(K = AM \cap SO\). Khi đó:
a) \(SO\) là giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\),\((ABC)\)
b) \(SO\) là giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\),\((SBD)\)
c) Giao điểm của đường thẳng \(SO\) với mặt phẳng \((ABM)\) là điểm \(K\)
d) Giao điểm của đường thẳng \(SD\) với mặt phẳng \((ABM)\) là điểm \(N\) thuộc đường thẳng \(AK\)
Cho hình bình hành ABCD và một điểm \(S\) không thuộc mặt phẳng \((ABCD)\), các điểm \(M,N\) lần lượt là trung điểm của đoạn thẳng \(AB,SC\). Gọi \(O = AC \cap BD\);
a) \(SO\) giao tuyến của hai mặt phẳng \((SAC)\) và \((SBD)\).
b) Giao điểm của \(I\) của đường thẳng \(AN\) và mặt phẳng \((SBD)\) là điểm nằm trên đường thẳng \(SO\)
c) Giao điểm của \(J\) của đường thẳng \(MN\) và mặt phẳng \((SBD)\) là điểm nằm trên đường thẳng \(SD\)
d) Ba điểm \(I,J,B\) thẳng hàng.
Cho tứ diện SABC. Gọi \(M\) và \(N\) lần lượt là hai điểm trên hai cạnh \(AB\) và \(BC\) sao cho \(MN\) không song song với \(AC\). Khi đó:
a) Đường thẳng \(MN\) cắt đường thẳng \(AC\)
b) Giao điểm của đường thẳng \(MN\) và mặt phẳng \((SAC)\) là giao điểm của \(MN\) và \(AC\).
c) Giao tuyến của hai mặt phẳng \((SMN)\) và \((SAC)\) là đường thẳng đi qua giao điểm của \(MN\) và \(AC\)
d) Giao tuyến của hai mặt phẳng \((SAN)\)và \((SCM)\) là đường thẳng đi qua giao điểm của \(MN\) và \(AC\).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hình tứ diện SABC và các điểm \({A^\prime },{B^\prime },{C^\prime }\) lần lượt thuộc các cạnh \(SA,SB\),\(SC\). Giả sử hai đường thẳng \({B^\prime }{C^\prime }\) và \(BC\) cắt nhau tại \(D\), hai đường thẳng \({C^\prime }{A^\prime }\) và \(CA\) cắt nhau tại \(E\) và hai đường thẳng \({A^\prime }{B^\prime }\) và \(AB\) cắt nhau tại \(F\). Chứng minh rằng ba điểm \(D,E,F\) thẳng hàng.
Bạn Huy đổ nước màu vào một chiếc bể cá có các mặt đều làm bằng kính phẳng. Sau một vài hôm nước bay hơi một phần và để lại trên thành bể các vêt màu như trong Hình 4.5.
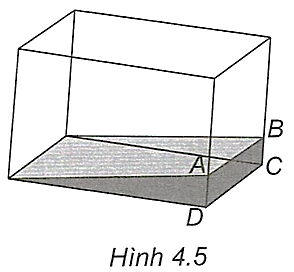
Huy quan sát thấy rằng, dù bể cá có hình dạng như thế nào, miễn là các mặt đều phẳng, thì vệt màu trên mỗi thành bể đều là các đường thẳng. Hãy giải thích vì sao.
Cho tứ diện ABCD. Gọi \(E,F,G\) lần lượt là các điểm thuộc ba cạnh \(AB,AC\), \(BD\) sao cho \(EF\) cắt \(BC\) tại \(I,AD\) cắt \(EG\) tại \(H\). Chứng minh ba đường thẳng \(CD\), \(IG,HF\) cùng đi qua một điểm.
Căng một sợi dây sao cho hai đầu của sợi dây nằm trên mặt bàn. Khi đó, sợi dây có nằm trên mặt bàn hay không?
Trong Hình 4.7, mặt nước và thành bể có giao nhau theo đường thẳng hay không?
Để tránh cho cửa ra vào không bị va đập vào các đồ dùng xung quanh (do mở cửa quá mạnh hoặc do gió to dập cửa), người ta thường sử dụng một phụ kiện là hít cửa nam châm. Hãy giải thích tại sao khi cửa được hút tới vị trí của nam châm thì cánh cửa được giữ cố định.







