Đề kiểm tra Đường thẳng và mặt phẳng trong không gian (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho tứ diện \(ABC{\rm{D}}\), \(G\) là trọng tâm tam giác \(BC{\rm{D}}\). Giao tuyến của \(\left( {AC{\rm{D}}} \right)\) và \(\left( {GAB} \right)\) là
\(AM\)(với \(M\) là trung điểm \(AB\)).
\(AN\) (với \(N\) là trung điểm \(C{\rm{D}}\)).
\(AK\) (với \(K\) là hình chiếu của \(C\)trên \(B{\rm{D}}\)).
\(AH\) (với \(H\) là hình chiếu của \(B\)trên \({\rm{CD}}\)).
Cho tứ diện ABCD. Lấy điểm \(M\) sao cho \(AM = 2CM\)và \(N\)là trung điểm \(AD\). Gọi \(O\)là một điểm thuộc miền trong của \(\Delta BCD\). Giao điểm của \(BC\) với \(\left( {OMN} \right)\) là giao điểm của \(BC\) với
\(OM\).
\(MN\).
\(A,B\) đều đúng.
\(A,B\) đều sai.
Cho tứ diện ABCD. Gọi \(M\) và \(N\) lần lượt là trung điểm của \(BC\) và \(AD\); \(G\) là trung điểm của \(MN\). Trong các khẳng định sau, khẳng định nào sai?
\(BG \cap \left( {ACD} \right) = B'\,\,;\,\,B'\)là trọng tâm tam giác \(ACD\).
\(G\)là trọng tâm tứ diện \(ABCD\).
\(AG \cap \left( {BCD} \right) = A'\,\,;\,\,A'\) là trọng tâm tam giác \(BCD\).
\(G\)là trọng tâm tam giác \(ADM\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi \(I\), \(J\), \(K\) lần lượt là trung điểm các cạnh \(SA\), \(BC\), \(CD\). Thiết diện của \(S.ABCD\) cắt bởi mặt phẳng \(\left( {IJK} \right)\) là
Hình tam giác.
Hình ngũ giác.
Hình lục giác.
Hình tứ giác.
Cho tứ diện ABCD. Gọi \(H,K\) lần lượt là trung điểm các cạnh\(AB,AC\). Trên đường thẳng \(CD\) lấy điểm \(M\) nằm ngoài đoạn \(CD\). Thiết diện của tứ diện với mặt phẳng \((HKM)\) là
Tứ giác \(HKMN\) với \(N \in AD\).
Hình thang \(HKMN\) với \(N \in AD\) và \(HK//MN\).
Tam giác \(HKL\) với \(L = KM \cap AD\).
Tam giác \(HKL\) với \(L = HM \cap AD\).
Cho tứ diện ABCD trong đó có tam giác BCD không cân. Gọi \[M,\,N\] lần lượt là trung điểm của \[AB,\,CD\] và \[G\] là trung điểm của đoạn \[MN\]. Gọi \[{A_1}\] là giao điểm của \[AG\] và \[\left( {BCD} \right)\]. Khẳng định nào sau đây đúng?
\({A_1}\) là tâm đường tròn tam giác \(BCD\).
\({A_1}\) là tâm đường tròn nội tiếp tam giác \(BCD\).
\({A_1}\) là trực tâm tam giác \(BCD\).
\({A_1}\) là trọng tâm tam giác \(BCD\).
Cho tứ diện ABCD. Gọi \(E\) và \(F\) lần lượt là trung điểm của \(AB\) và \(CD\); \(G\) là trọng tâm của tam giác \(BCD\). Giao điểm của đường thẳng \(EG\) và mặt phẳng \(\left( {ACD} \right)\) là
Điểm \(F\).
Giao điểm của đường thẳng \(EG\) và \(AF\).
Giao điểm của đường thẳng \(EG\) và \(AC\).
Giao điểm của đường thẳng \(EG\) và \(CD\).
Cho hình chóp tứ giác S.ABCD và một mặt phẳng \(\left( P \right)\) thay đổi. Thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\) là một đa giác có số cạnh nhiều nhất có thể là:
\(5\) cạnh.
\(4\) cạnh.
\(3\) cạnh.
\(6\) cạnh.
Cắt hình chóp tứ giác bởi mặt phẳng vuông góc với đường cao của hình chóp thiết diện là hình gì?
Một hình bình hành.
Một ngũ giác.
Một hình tứ giác.
Một hình tam giác.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi \[M\] và \[N\]lần lượt là trung điểm của \[SA\] và\[SC\]. Mặt phẳng \[\left( {BMN} \right)\]cắt \[AD,CD\] lần lượt tại \[E,F\]. Khẳng định nào sau đây đúng?
\(A,E,F\)thẳng hàng.
\(B,E,F\)thẳng hàng.
\(C,E,F\)thẳng hàng.
\(D,E,F\)thẳng hàng.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (MNP) là
Tứ giác.
Tam giác.
Ngũ giác.
Lục giác.
Cho hình tứ diện ABCD có \[M\], \[N\]lần lượt là trung điểm của \[AB\], \[BD\]. Các điểm \[G\], \[H\] lần lượt trên cạnh \[AC\], \[CD\] sao cho \[NH\]cắt \[MG\] tại \[I\]. Khẳng định nào sau đây là khẳng đỉnh đúng?
\(A\), \[C\], \[I\] thẳng hàng.
\[B\], \(C\), \[I\] thẳng hàng.
\(N\), \(G\), \[H\] thẳng hàng.
\(B\), \[G\], \[H\] thẳng hàng.
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong các mệnh đề sau đây, mệnh đề nào sai?
a) Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa\[.\]
b) Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất\[.\]
c) Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất\[.\]
d) Hai mặt phẳng cùng đi qua 3 điểm \(A,\;B,\;C\) không thẳng hàng thì hai mặt phẳng đó trùng nhau
Cho tứ diện ABCD. Gọi \(I,J\) lần lượt là trung điểm của \(AD,BC\), \(M\) là một điểm trên cạnh \(AB,N\) là một điểm trên cạnh \(AC\). Khi đó:
a) \[IJ\] là giao tuyến của hai mặt phẳng \((IBC),(JAD)\).
b) \(ND\) là giao tuyến của hai mặt phẳng \((MND),(ADC)\).
c) \(BI\) là giao tuyến của hai mặt phẳng \((BCI),(ABD)\).
d) Giao tuyến của hai mặt phẳng \((IBC),(DMN)\) song song với đường thẳng \[IJ\].
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi \(M\) là trung điểm của \(SC\). Gọi \(I\) giao điểm của đường thẳng \(AM\) và mặt phẳng \((SBD)\). Khi đó:
a) \(AM \cap SO = I\).
b) \(IA = 3IM\).
c) Giao điểm \(E\) của đường thẳng \(SD\) và mặt phẳng \((ABM)\) là điểm thuộc đường thẳng \(BI\)
d) Gọi \(N\) là một điểm tuỳ ý trên cạnh \(AB\). Khi đó giao điểm của đường thẳng \(MN\) và mặt phẳng \((SBD)\) là điểm thuộc giao tuyến của hai mặt phẳng \((SBD),(SNC)\)
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi \(O\) là giao điểm của \(AC\) và \(BD;M,N\) lần lượt là trung điểm của \(SB,SD;P\) thuộc đọan \(SC\) và không là trung điểm của \(SC\).Khi đó:
a) Giao điểm \(E\) của đường thẳng \(SO\) và mặt phẳng \((MNP)\) là giao điểm của \(MN\) và \(SO\).
b) Giao điểm \(Q\) đường thẳng \(SA\) và mặt phẳng \((MNP)\) là giao điểm của \(PE\) và \(SO\).
c) Gọi \(I,J,K\) lần lượt là giao điểm của \(QM\) và \(AB,QP\) và \(AC,QN\) và \(AD\). Vậy \(I,J,K\) thẳng hàng.
d) Gọi \(I,J,K\) lần lượt là giao điểm của \(QM\) và \(AB,QP\) và \(AC,QN\) và \(AD\). Vậy \(I,J,K\) không thẳng hàng.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho tứ diện ABCD. Trên các cạnh AB,AC,BD lần lượt lấy các điểm \(E,F,G\) sao cho EB > AE,AF > FC,BG > GD. Tìm giao tuyến của các cặp mặt phẳng (EFG) và \((ACD),(EFG)\) và \((BCD),(EFG)\) và \((ABD)\).
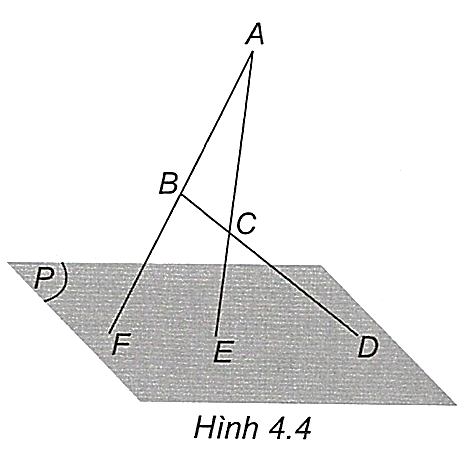
Cho mặt phẳng \((P)\) và ba điểm \(A,B,C\) phân biệt nằm ngoài mặt phẳng \((P)\). Giả sử các đường thẳng \(BC,CA,AB\) lần lượt cắt mặt phẳng \((P)\) tại \(D,E,F(\)H.4.4). Chứng minh rằng ba điểm \(D,E,F\) thẳng hàng.
Đánh dấu một điểm trên mép của tờ giấy \(A4\) và dùng kéo cắt một đường bất kì đi qua điểm đó (trong khi cắt không xoay kéo). Hãy giải thích vì sao đường cắt nhận được trên tờ giấy luôn là đường thẳng.
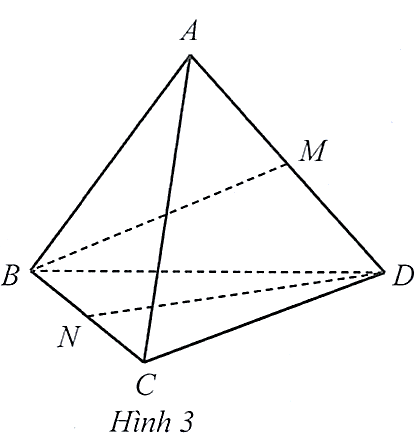
Cho tứ diện ABCD. Các điểm \(M,N\) lần lượt là trung điểm của các cạnh \(AD\) và \(BC\) (Hình 3). Hỏi bốn điểm \(B,M,D,N\) có cùng thuộc một mặt phẳng hay không?
Trong Hình \(4.4\) là một khối rubik có bốn đỉnh và bốn mặt, mỗi mặt là một tam giác.

a) Đặt khối rubik sao cho ba đỉnh của mặt màu đỏ đều nằm trên mặt bàn. Khi đó, mặt màu đỏ của khối rubik có nằm trên mặt bàn hay không?
b) Có thể đặt khối rubik sao cho bốn đỉnh của nó đều nằm trên mặt bàn hay không?
Hãy giải thích tại sao trong thực tiễn có nhiều đồ vật được thiết kế gồm ba chân như chân đỡ máy ảnh, giá treo tranh, kiềng ba chân treo nồi,...







