35 CÂU HỎI
Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:

Mẫu số liệu được chia thành bao nhiêu nhóm?
A. 6 nhóm.
B. 5 nhóm.
C. 7 nhóm.
D. 8 nhóm.
Tìm hiểu thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:

Có bao nhiêu học sinh có thời gian xem ti vi từ 20 giờ đến dưới 25 giờ trong tuần trước?
A.\(8\).
B. \(16\).
C. \(4\).
D. \(2\).
Kết quả khảo sát cân nặng của 25 quả cam ở lô hàng A được cho ở bảng sau:

Nhóm chứa mốt là nhóm nào.
A.\(\left[ {150;155} \right)\).
B.\(\left[ {155;160} \right)\).
C.\(\left[ {165;170} \right)\).
D.\(\left[ {170;175} \right)\).
Cân nặng của 28 học sinh nam lớp 11 được cho trong bảng sau:

Số trung bình của mẫu số liệu ghép nhóm trên xấp xỉ bằng
A.\(55,6\).
B. \(65,5\).
C. \(48,8\).
D. \(57,7\).
Một hộp đựng 9 tấm thẻ cùng loại được ghi các số từ 1 đến 9. Rút ngẫu nhiên một tấm thẻ. Xét biến cố A “ Số ghi trên tấm thẻ rút ra là số lẻ”. Chọn mệnh đề đúng?
A.\[A = \{ 1;2;3;4;5;6;7;8;9\} \].
B.\(A = \{ 1;3;5;7;9\} \).
C.\(A = \{ 2;4;6;8\} \).
D.\(A = \{ 1;9\} \).
Gọi \(X\)={\(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\)}. Chọn ngẫu nhiên một số từ tập \(X\). Tính xác suất để số được chọn là số lẻ.
A.\(\frac{1}{2}\).
B.\(\frac{1}{3}\).
C.\(\frac{1}{4}\).
D.\(\frac{1}{5}\).
Có hai xạ thủ cùng thi bắn một mục tiêu. Xác suất để xạ thủ 1 bắn trúng mục tiêu là\(0,5\). Xác suất để xạ thủ 2 bắn trúng mục tiêu là\(0,7\). Xác suất để cả 2 xạ thủ bắn trúng mục tiêu là
A.\(0,35\).
B.\(0,5\).
C.\(0,7\).
D. \(0,65\).
Cho \(x,\,y\) là hai số thực dương và \(m,\,n\) là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
A. \({x^m}.{x^n} = {x^{m + n}}\).
B. \({\left( {xy} \right)^n} = {x^n}.{y^n}\).
C. \({\left( {{x^n}} \right)^m} = {x^{nm}}\).
D.\({x^m}.{y^n} = {\left( {xy} \right)^{m + n}}\).
Cho hai số dương \[a,b(a \ne 1)\]. Mệnh đề nào dưới đây SAI?
A. \[{\log _a}{a^\alpha } = \alpha \].
B. \[{\log _a}1 = 0\].
C. \[{\log _a}a = 2a\].
D.\({\log _{{a^\alpha }}}b = \frac{1}{\alpha }{\log _a}b\).
Nếu \({\log _a}x = \frac{1}{2}{\log _a}9 - {\log _a}5 + {\log _a}2\)\(\left( {a > 0,a \ne 1} \right)\) thì \(x\) bằng:
A. \(\frac{2}{5}\).
B. \(\frac{3}{5}\).
C. \(\frac{6}{5}\).
D. \(3\).
Hàm số nào sau đây là hàm số mũ
A. \(y = {2^{\frac{x}{2}}}\).
B.\(y = - {2^x}\).
C. \(y = {x^{ - 2}}\).
D.\(y = {x^2}\).
Số nghiệm của phương trình \({3^{{x^2} - x}} = 9\) là
A.\(2.\)
B. \(0.\)
C. \(1.\)
D.\(3.\)
Tập nghiệm của bất phương trình \({\log _2}\left( {3x + 1} \right) < 2\) là
A. \(\left[ { - \frac{1}{3};1} \right)\).
B. \(\left( { - \frac{1}{3};\frac{1}{3}} \right)\).
C. \(\left( { - \frac{1}{3};1} \right)\).
D. \(\left( { - \infty ;1} \right)\).
Tổng các giá trị nghiệm của phương trình \(\log _{\frac{1}{2}}^2x - 5{\log _2}x + 6 = 0\) bằng
A. \(10\).
B. \(\frac{{65}}{{64}}\).
C. \(5\).
D. \(\frac{{129}}{{64}}\).
Cho hàm số \(y = f(x)\) có đồ thị \((C)\) và đạo hàm \(f'(2) = 6.\) Hệ số góc của tiếp tuyến của \((C)\) tại điểm \(M\left( {2;f\left( 2 \right)} \right)\) bằng
A. \(2\).
B. \(3\).
C. \(6\).
D. \(12\).
Phương trình tiếp tuyến với đồ thị hàm số \(y = {x^2} + 2x\;\)tại điểm\({\rm{\;}}{x_{0\;}} = 1{\rm{\;l\`a }}\):
A.\(y = 4x + 2\).
B.\({\rm{\;}}y = 4x\).
C.\(y = 4x - 4\).
D. \(y = 4x - 1\).
Hàm số \(y = \cot x\) có đạo hàm là:
A. \(y' = - \frac{1}{{{{\cos }^2}x}}.\)
B. \(y' = - \frac{1}{{{{\sin }^2}x}}.\)
C. \(y' = 1 + {\cot ^2}x\).
D. \(y' = - \tan x\).
Đạo hàm của hàm số \(y = {3^x}\)là
A. \(y' = x{.3^{x - 1}}\).
B. \(y' = {3^x}.\ln 3\).
C. \(y' = {3^x}\).
D. \(y' = \frac{{{3^x}}}{{\ln 3}}\).
Đạo hàm của hàm số \[y = \sqrt x + x\] tại điểm \[{x_0} = 4\] là:
A. \[y'(4) = \frac{3}{2}\].
B. \[y'(4) = \frac{9}{2}\].
C. \[y'(4) = \frac{5}{4}\].
D. \[y'(4) = 6\].
Hàm số \(y = {x^5}\) có đạo hàm cấp 2 là
A. \[5{x^4}\].
B. \(20x\).
C. \(20{x^3}\).
D. \(5{x^3}\).
Hàm số \(y = \frac{1}{{x + 1}}\) có đạo hàm cấp hai tại \(x = 1\) là
A. \[y''\left( 1 \right) = \frac{1}{2}\].
B. \(y''\left( 1 \right) = - \frac{1}{4}\).
C. \(y''\left( 1 \right) = 4\).
D. \(y''\left( 1 \right) = \frac{1}{4}\).
Cho \(y = \sqrt {2x - {x^2}} \), tính giá trị của biểu thức \(A = {y^3}.y''\).
A. \[1\].
B. \(0\).
C. \( - 1\).
D.\( - 5\).
Cho hình chóp \[S.ABC\]có \[SA \bot (ABC)\]và \[H\] là hình chiếu vuông góc \[S\] của lên \[BC\]. Hãy chọn khẳng định đúng?
A. \[BC \bot AC\].
B. \[BC \bot AB\].
C. \[BC \bot SC\].
D. \[BC \bot AH\].
Trong không gian cho điểm \(A\) và mặt phẳng \((P).\) Mệnh đề nào dưới đây đúng?
A. Có đúng một đường thẳng đi qua \(A\) và vuông góc với \((P).\)
B. Có đúng hai đường thẳng đi qua \(A\) và vuông góc với \((P).\)
C. Có vô số đường thẳng đi qua \(A\) và vuông góc với \((P).\)
D. Không tồn tại đường thẳng đi qua \(A\) và vuông góc với \((P).\)
Cho hình chóp A.ABC có SC vuông góc với (ABC). Góc giữa SA với (ABC) là góc giữa:
A. \[SA\]và \[AB\].
B.\[SA\]và \[SC\].
C.\[SB\]và\[BC\].
D. \[SA\]và \[AC\].
Cho hình lăng trụ đều \(ABC.A'B'C'\) có \(AB = \sqrt 3 \) và \(AA' = 1\). Góc tạo bởi giữa đường thẳng \(AC'\) và \(\left( {ABC} \right)\) bằng.
A. \[45^\circ \].
B. \(60^\circ \).
C. \(30^\circ \).
D.\(75^\circ \).
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông, \(SA\) vuông góc với mặt phẳng đáy. Mặt phẳng \(\left( {ABCD} \right)\) vuông góc với mặt phẳng nào dưới đây ?
A.\((SAC).\)
B.\((SBD).\)
C.\((SCD).\)
D.\((SBC).\)
Khẳng định nào sau đây đúng?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng song song khi và chỉ khi góc giữa chúng bằng \(0^\circ \).
D. Hai đường thẳng trong không gian cắt nhau khi và chỉ khi góc giữa chúng lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \).
Cho hình lăng trụ tứ giác đều \(ABCD.A'B'C'D'\). Mặt phẳng \(\left( {AB'C} \right)\) vuông góc với mặt phẳng nào sau đây?
A.\(\left( {D'BC} \right)\).
B.\(\left( {B'BD} \right)\).
C.\(\left( {D'AB} \right)\).
D.\(\left( {BA'C'} \right)\).
Cho hình lập phương \(ABCD.A'B'C'D'\) như hình vẽ bên
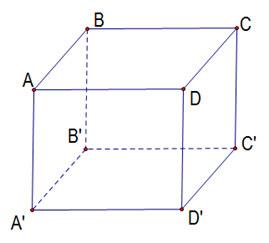
Hình chiếu của \(A\) trên mặt phẳng \(\left( {A'B'C'D'} \right)\)là
A.\(A'.\)
B.\(B'.\)
C.\(C'.\)
D.\(D'.\)
Cho khối lập phương \(ABCD.A'B'C'D'\). Đoạn vuông góc chung của hai đường thẳng chéo nhau \(AD\) và \(A'C'\) là
A.\[AA'.\]
B.\[BB'.\]
C.\[DA'.\]
D.\(DD'.\)
Cho hình lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh đều bằng \(a\). Góc tạo bởi cạnh bên và mặt phẳng đáy bằng \(30^\circ \). Hình chiếu \(H\) của \(A\) trên mặt phẳng \(\left( {A'B'C'} \right)\) là trung điểm của \(B'C'\). Tính theo \(a\) khoảng cách giữa hai mặt phẳng đáy của lăng trụ \(ABC.A'B'C'\).
A.\[\frac{a}{2}.\]
B.\[\frac{a}{3}.\]
C.\[\frac{{a\sqrt 3 }}{2}.\]
D.\(\frac{{a\sqrt 2 }}{2}.\)
Cho hình chóp \[S.ABC\]có chiều cao bằng\[3\], đáy\[ABC\] có diện tích bằng\[10\]. Thể tích khối chóp \[S.ABC\] bằng:
A. \[2\].
B. \[30\].
C. \[10\].
D. \[15\].
Trong các mệnh đề dưới đây, mệnh đề nào sai?
A. Hình chóp tứ giác đều có tất cả các cạnh bằng nhau.
B. Hình chóp tứ giác đều có các cạnh bên bằng nhau.
C. Hình chóp tứ giác đều có đáy là hình vuông.
D. Hình chóp tứ giác đều có hình chiếu vuông góc của đỉnh lên đáy trùng với tâm của đáy.
Cho khối chóp \(S.ABC\) có \(SA\) vuông góc với đáy, \(SA = 4,AB = 6,BC = 10,CA = 8\). Tính thể tích của khối chóp \(S.ABC\).
A. \[V = 32\].
B. \[V = 192\].
C. \[V = 40\].
D. \[V = 24\].

