35 CÂU HỎI
Khảo sát thời gian chạy bộ trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
|
Thời gian (phút) |
\([0;20)\) |
\([20;40)\) |
\([40;60)\) |
\([60;80)\) |
\([80;100)\) |
|
Số học sinh |
\(5\) |
\(9\) |
\(12\) |
\(10\) |
\(6\) |
Mẫu số liệu ghép nhóm này có mốt là
A. \(59.\)
B.\(40.\)
C.\(52.\)
D.\(53.\)
Người ta tiến hành phỏng vấn 40 người về một mẫu áo khoác. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm là \(100.\) Kết quả được trình bày trong bảng ghép nhóm sau:
|
Nhóm |
\(\left[ {50;60} \right)\) |
\(\left[ {60;70} \right)\) |
\(\left[ {70;80} \right)\) |
\(\left[ {80;90} \right)\) |
\(\left[ {90;100} \right)\) |
|
|
Tần số |
\(4\) |
\(5\) |
\(23\) |
\(6\) |
\(2\) |
\(N = 40\) |
Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị
A. \(74\).
B.\[75.\]
C.\[76.\]
D.\[77.\]
Khẳng định nào sau đây là ĐÚNG:
A. Cho hai biến cố \(A\) và \(B\). Biến cố "\(A\) hoặc \(B\) xảy ra", kí hiệu là \(A \cup B\), được gọi là biến cố giao của \(A\) và \(B\).
B. Cho hai biến cố \(A\) và \(B\). Biến cố "\(A\) hoặc \(B\) xảy ra", kí hiệu là \(A \cap B\), được gọi là biến cố hợp của \(A\) và \(B\).
C. Cho hai biến cố \(A\) và \(B\). Biến cố "\(A\) hoặc \(B\) xảy ra", kí hiệu là \(A \cup B\), được gọi là biến cố hợp của \(A\) và \(B\).
D. Cho hai biến cố \(A\) và \(B\). Biến cố "\(A\) hoặc \(B\) xảy ra", kí hiệu là \(A \cup B\), được gọi là biến cố xung khắc.
Cho A và B là 2 biến cố độc lập với nhau, \(P\left( A \right) = 0,4;\,\,\,P\left( B \right) = 0,3.\) Khi đó \(P\left( {A.B} \right)\) bằng
A. 0,58.
B. 0,7.
C. 0,1.
D. 0,12.
Cho \[A,B\] là hai biến cố xung khắc. Biết \(P\left( A \right) = \frac{1}{5}\), \(P\left( {A \cup B} \right) = \frac{1}{3}\). Tính \[P\left( B \right).\]
A. \[\frac{3}{5}\].
B. \[\frac{8}{{15}}\].
C. \[\frac{2}{{15}}\].
D. \[\frac{1}{{15}}\].
Chọn ngẫu nhiên \[2\] đỉnh của một hình bát giác đều nội tiếp trong đường tròn tâm \(O\) bán kính \(R\). Xác suất để khoảng cách giữa hai đỉnh đó bằng \(R\sqrt 2 \) là
A. \(\frac{2}{7}\).
B. \(\frac{3}{7}\).
C. \(\frac{4}{7}\).
D. \(\frac{5}{{56}}\).
Một hộp đựng 5 quả cầu màu xanh và 3 quả cầu màu đỏ, có cùng kích thước và khối lượng. Chọn ngẫu nhiên hai quả cầu trong hộp. Tính xác suất để chọn được hai quả cầu có cùng màu.
A. \(\frac{{10}}{{28}}\).
B. \(\frac{3}{{28}}\).
C. \(\frac{{13}}{{28}}\).
D. \(\frac{7}{{28}}\).
Hai người cùng bắn vào 1 bia. Người thứ nhất có xác suất bắn trúng là 60%, xác suất bắn trúng của người thứ 2 là 70%. Xác suất để cả hai người cùng bắn không trúng bằng
A.\[\frac{1}{{12}}\].
B.\[\frac{{11}}{{12}}\].
C.\[\frac{1}{2}\].
D.\[\frac{3}{{25}}\].
Cho\[a > 0\], \[b > 0\] và \[x\], \[y\] là các số thực bất kỳ. Đẳng thức nào sau đúng?
A. \({\left( {a + b} \right)^x} = {a^x} + {b^x}\).
B. \({\left( {\frac{a}{b}} \right)^x} = {a^x}.{b^{ - x}}\).
C. \({a^{x + y}} = {a^x} + a{}^y\).
D. \({a^x}{b^y} = {\left( {ab} \right)^{xy}}\).
Cho biểu thức \(P = \sqrt[4]{{{x^2}\sqrt[3]{x}}}\), \(\left( {x > 0} \right)\). Mệnh đề nào dưới đây đúng?
A. \[P = {x^{\frac{6}{{12}}}}\].
B. \(P = {x^{\frac{8}{{12}}}}\).
C. \(P = {x^{\frac{9}{{12}}}}\).
D. \(P = {x^{\frac{7}{{12}}}}\).
Cho \(a = {3^{\sqrt 5 }},b = {3^2},c = {3^{\sqrt 6 }}\). Mệnh đề nào dưới đây đúng?
A. \(a < b < c\).
B. \(a < c < b\).
C.\(c < a < b\).
D.\(b < a < c.\)
Giá trị của biểu thức \({\log _4}2\)là:
A. 1.
B. 2.
C. \(\frac{3}{2}\).
D. \(\frac{1}{2}\).
Cho \(a\), \(b\), \(c\) là các số dương và \(a \ne 1\), khẳng định nào sau đây sai?
A. \({\log _a}\left( {b + c} \right) = {\log _a}b.{\log _a}c\).
B. \({\log _a}\left( {\frac{b}{c}} \right) = {\log _a}b - {\log _a}c\).
C. \({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\).
D. \({\log _a}\left( {\frac{1}{b}} \right) = - {\log _a}b\).
Trong các hàm số sau, hàm số nào là hàm số mũ?
A. \(y = {x^4}\).
B. \(y = {\left( \pi \right)^x}\).
C. \(y = {\log _2}x\).
D. \(y = {\left( {x - 1} \right)^{ - 2}}\).
Đồ thị sau là của hàm số nào?
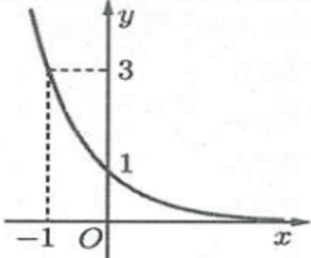
A. \(y = {\left( {\sqrt 3 } \right)^x}\).
B. \(y = {\left( {\frac{1}{2}} \right)^x}\).
C. \(y = {\log _{\frac{1}{3}}}x\).
D. \(y = {\left( {\frac{1}{3}} \right)^x}\).
Ông An gửi 100 triệu đồng vào tiết kiệm ngân hàng theo thể thức lãi kép trong một thời gian khá lâu mà không rút ra với lãi suất ổn định trong mấy chục năm qua là 10%/1 năm. Tết năm nay do ông kẹt tiền nên rút hết ra để gia đình đón Tết. Sau khi rút cả vốn lẫn lãi, ông trích ra gần 10 triệu đồng để mua đồ Tết trong nhà thì ông còn 250 triệu đồng. Hỏi ông đã gửi tiết kiệm bao nhiêu lâu?
A. 10 năm.
B. 17 năm.
C. 15 năm.
D. 20 năm.
Tìm tập nghiệm\[S\]của phương trình \({2^{x + 1}} = 8\).
A.\(S = \left\{ 1 \right\}\).
B.\(S = \left\{ { - 1} \right\}\).
C.\(S = \left\{ 4 \right\}\).
D.\(S = \left\{ 2 \right\}\).
Số nghiệm của phương trình \({\log _3}\left( {{x^2} + 4x} \right) + {\log _{\frac{1}{3}}}\left( {2x + 3} \right) = 0\) là
A.\(2\).
B. \(3\).
C. \(0\).
D. \(1\).
Giới hạn (nếu tồn tại) nào sau đây dùng để định nghĩa đạo hàm của hàm số \(y = f(x)\)tại\[{x_0}\]?
A. \[\mathop {{\rm{lim}}}\limits_{\Delta x \to 0} \frac{{f(x + \Delta x) - f({x_0})}}{{\Delta x}}\].
B. \[\mathop {{\rm{lim}}}\limits_{x \to 0} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\].
C. \[\mathop {{\rm{lim}}}\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\].
D. \[\mathop {{\rm{lim}}}\limits_{\Delta x \to 0} \frac{{f({x_0} + \Delta x) - f(x)}}{{\Delta x}}\].
Cho hàm số \(f\left( x \right) = {x^2} + 1\). Tính đạo hàm của hàm số tại điểm \({x_0} = 2\).
A. \(3.\)
B. \(4.\)
C. \(2.\)
D. \(5.\)
Giả sử \(u = u(x),\,\,v = v(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Đạo hàm của hàm số \(y = \frac{u}{v}\,\,\left( {v = v(x) \ne 0} \right)\) là
A. \(y' = \frac{{u.v' - u'.v}}{v}\).
B. \(y' = \frac{{u'.v - v'.u}}{v}\).
C. \(y' = \frac{{u.v' - u'.v}}{{{v^2}}}\).
D. \(y' = \frac{{u'.v - v'.u}}{{{v^2}}}\).
Giả sử \(\,v = v(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Đạo hàm của hàm số \(y = \frac{1}{v}\,\,\left( {v = v(x) \ne 0} \right)\) là
A. \(y' = \frac{{{v^'}}}{v}\).
B. \(y' = \frac{{v'}}{{{v^2}}}\).
C. \(y' = - \frac{{v'}}{{{v^{}}}}\).
D. \(y' = - \frac{{v'}}{{{v^2}}}\).
Trong các công thức sau, công thức nào đúng?
A. \({\left( {\sin x} \right)^\prime } = \cos x.\)
B. \({\left( {\sin x} \right)^\prime } = - \cos x.\)
C. \({\left( {\cos x} \right)^\prime } = \sin x.\)
D. \({\left( {\sin x} \right)^\prime } = \sin x.\)
Đạo hàm của hàm số \(y = {\left( {{x^2} + 3} \right)^5}\) là
A. \(y' = 2x{\left( {{x^2} + 3} \right)^4}.\)
B. \(y' = 5{\left( {{x^2} + 3} \right)^4}.\)
C. \(y' = 10x{\left( {{x^2} + 3} \right)^4}.\)
D. \(y' = 2x{\left( {{x^2} + 3} \right)^5}.\)
Đạo hàm của hàm số \[y = \cot \left( {2x - 1} \right)\] là
A.\[\frac{2}{{{{\sin }^2}\left( {2x - 1} \right)}}\].
B.\[ - \frac{2}{{{{\sin }^2}\left( {2x - 1} \right)}}\].
C.\[\frac{1}{{{{\sin }^2}\left( {2x - 1} \right)}}\].
D.\[\frac{2}{{{{\cos }^2}\left( {2x - 1} \right)}}\].
Đạo hàm cấp hai của hàm số \[f\left( x \right) = {x^2}\] bằng biểu thức nào sau đây?
A. \[2\].
B. \[x\].
C. \[3\].
D. \[2x\].
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Khẳng định nào sau đây sai?
A. Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau nằm trong \(\left( \alpha \right)\)thì \(d\) vuông góc với bất kì đường thẳng nào nằm trong \(\left( \alpha \right)\).
B. Nếu đường thẳng \(d \bot \left( \alpha \right)\) thì \(d\) vuông góc với hai đường thẳng trong \(\left( \alpha \right)\).
C. Nếu đường thẳng \(d\) vuông góc với hai đường thẳng nằm trong \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right).\)
D. Nếu \(d \bot \left( \alpha \right)\) và đường thẳng \(a//\left( \alpha \right)\) thì \(d \bot a\).
Cho tứ diện \(OABC\) có \(OA\), \(OB\), \(OC\) đôi một vuông góc với nhau. Gọi \(H\) là hình chiếu của \(O\) trên mặt phẳng \(\left( {ABC} \right)\). Mệnh đề nào sau đây đúng?
A. \(H\) là trung điểm của \(AC\).
B. \(H\) là trọng tâm tam giác \(ABC\).
C. \(H\) là trung điểm của \(BC\).
D. \(H\) là trực tâm của tam giác \(ABC\).
Khẳng định nào ĐÚNG trong các khẳng định sau:
A. Nếu đường thẳng \(a\) cắt một đường thẳng \(d \subset \left( P \right)\) thì góc giữa \(a\) và \(d\) là góc giữa đường thẳng \(a\) và \((P)\).
B. Nếu đường thẳng \(a\) không vuông góc với \((P)\)thì góc giữa \(a\) và hình chiếu \(a'\) của \(a\) trên \((P)\) gọi là góc giữa đường thẳng \(a\) và \((P)\).
C. Nếu đường thẳng \(a\) vuông góc với đường thẳng \(d \subset \left( P \right)\) thì góc giữa \(a\) và \(d\) là góc giữa đường thẳng \(a\) và \((P)\).
D. Nếu đường thẳng \(a\) song song với đường thẳng \(d \subset \left( P \right)\) thì góc giữa \(a\) và \(d\) là góc giữa đường thẳng \(a\) và \((P)\).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Giá trị \(\sin \) của góc nhị diện \(\left[ {A',BD,A} \right]\)
A. \(\frac{{\sqrt 3 }}{4}\).
B. \(\frac{{\sqrt 6 }}{4}\).
C. \(\frac{{\sqrt 6 }}{3}\).
D.\(\frac{{\sqrt 3 }}{3}\).
Hai mặt phẳng được gọi là vuông góc với nhau nếu
A. mọi đường thẳng nằm trong mặt phẳng này đều vuông góc với mặt phẳng kia.
B. mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
C. mặt phẳng này chứa một đường thẳng song song với mặt phẳng kia.
D. mọi đường thẳng nằm trong mặt phẳng này đều song song với mặt phẳng kia.
Đường vuông góc chung của hai đường thẳng chéo nhau \(a\) và \(b\) là:
A. Đường thẳng vừa vuông góc với \(a\) và vuông góc với \(b\).
B. Đường thẳng vừa vuông góc, vừa cắt hai đường thẳng chéo nhau \(a\) và \(b\).
C. Đường thẳng vuông góc với \(a\) và cắt đường thẳng \(b\).
D. Đường thẳng vuông góc với \(b\) và cắt đường thẳng \(a\).
Cho khối chóp diện tích đáy bằng \(S\) và chiều cao \(h\). Khi đó thể tích \(V\) của khối chóp bằng:
A. \(V = \frac{1}{2}S.h\).
B. \(V = \frac{1}{3}S.h\).
C. \(V = S.h\).
D. \(V = \frac{1}{6}S.h\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) và \(AB = 2a\). Tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích \(V\) của khối chóp \(S.ABC\)
A. \(V = \frac{{{a^3}\sqrt 3 }}{4}\).
B. \(V = \frac{{{a^3}\sqrt 3 }}{3}\).
C. \(V = \frac{{{a^3}\sqrt 3 }}{{12}}\).
D. \(V = \frac{{2{a^3}\sqrt 3 }}{3}\).

