35 CÂU HỎI
Giá trị của $\cot \frac{{89\pi }}{6}$ là
v
A.$\sqrt 3 $.
B.$ - \sqrt 3 $.
C.\[\frac{{\sqrt 3 }}{3}\].
D.\[ - \frac{{\sqrt 3 }}{3}\].
Biểu thức$\sin x\cos y - \cos x\sin y$ bằng
A.$\cos \left( {x - y} \right)$.
B.$\cos \left( {x + y} \right)$.
C.$\sin \left( {x - y} \right)$.
D.$\sin \left( {y - x} \right)$.
Tìm tập xác định $D$ của hàm số $y = \frac{{1 + \sin x}}{{\cos x - 1}}.$
A. $D = \mathbb{R}.$
B. $D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.$
C. $D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.$
D.$D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}.$
Phương trình $\sin x = \frac{{\sqrt 3 }}{2}$ có nghiệm là
A.$x = \pm \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}$.
B.$x = \frac{\pi }{3} + k\pi ,k \in \mathbb{Z}$.
C.$\left[ \begin{gathered}
x = \frac{\pi }{6} + k\pi \hfill \\
x = \frac{{5\pi }}{6} + k\pi \hfill \\
\end{gathered} \right.,k \in \mathbb{Z}$.
D.$\left[ \begin{gathered}
x = \frac{\pi }{3} + k2\pi \hfill \\
x = \frac{{2\pi }}{3} + k2\pi \hfill \\
\end{gathered} \right.,k \in \mathbb{Z}$.
Trong các dãy số sau dãy số nào là dãy số tăng?
A. $4;\,9;\,14;\,19;\,24$.
B. $9;\,7 & ;\,5;\,3;\,1;\,0$.
C. $\frac{1}{2};\,\frac{2}{5};\,\frac{3}{7};\,\frac{4}{9};\,\frac{5}{{12}}$.
D. \[0;\,1;\,2;\, - 3;\,7\].2
Dãy số nào sau đây là một cấp số cộng?
A.\[\left( {{u_n}} \right):\left\{ \begin{gathered}
{u_1} = 1 \hfill \\
{u_{n + 1}} = {u_n} + 2,\forall n \geqslant 1 \hfill \\
\end{gathered} \right.\].
B.\[\left( {{u_n}} \right):\left\{ \begin{gathered}
{u_1} = 3 \hfill \\
{u_{n + 1}} = 2{u_n} + 1,\forall n \geqslant 1 \hfill \\
\end{gathered} \right.\].
C.\[\left( {{u_n}} \right):1;3;6;10;15;...\].
D.\[\left( {{u_n}} \right): - 1;1; - 1;1; - 1;...\].
Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_4} = - 12$ và ${u_{14}} = 18$. Tính tổng 16 số hạng đầu tiên của cấp số cộng này.
A.\[{S_{16}} = - 24\].
B.\[{S_{16}} = 26\].
C.\[{S_{16}} = - 25\].
D.\[{S_{16}} = 24\].
Cho cấp số nhân $\left( {{u_n}} \right)$ với ${u_1} = - 2$ và $q = - 5$. Viết bốn số hạng đầu tiên của cấp số nhân.
A.\[ - 2;10;50; - 250\].
B.\[ - 2;10; - 50;250\].
C.\[ - 2; - 10; - 50; - 250\].
D.\[ - 2;10;50;250\].
Phát biểu nào sau đây là sai?
A.\[\lim {u_n} = c\](${u_n} = c$là hằng số).
B.\[\lim {q^n} = 0\left( {\left| q \right| > 1} \right)\].
C.\[\lim \frac{1}{n} = 0\].
D.\[\lim \frac{1}{{{n^k}}} = 0\left( {k > 1} \right)\].
Tính $L = \lim \frac{{n - 1}}{{{n^3} + 3}}$.
A.\[L = 1\].
B.\[L = 3\].
C.\[L = 0\].
D.\[L = 2\].
Cho $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty $, trong bốn khẳng định sau đây, khẳng định nào sai?
A. Tồn tại số thực $a > 0$ sao cho $f\left( a \right) < 0$.
B.\[\mathop {\lim }\limits_{x \to + \infty } \left[ { - f\left( x \right)} \right] = + \infty \].
C.\[\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{f\left( x \right)}} = 0\].
D.\[\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty \].
Cho các giới hạn: $\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = 2$; $\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 3$, hỏi $\mathop {\lim }\limits_{x \to {x_0}} \left[ {3f\left( x \right) - 4g\left( x \right)} \right]$ bằng
A.$5$.
B.$2$.
C.$ - 6$.
D.$3$.
Giới hạn $\mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - x + 7} \right)$ bằng?
A.\[5\].
B.\[9\].
C.\[0\].
D.\[7\].
Tìm $\mathop {\lim }\limits_{x \to {1^ + }} \frac{{4x - 3}}{{x - 1}}$
A.$ + \infty $.
B.\[2\].
C.\[ - \infty \].
D.\[ - 2\].
Trong bốn giới hạn sau đây, giới hạn nào bằng $ - \infty $?
A.$\mathop {\lim }\limits_{x \to + \infty } \frac{{ - 3x + 4}}{{x - 2}}$.
B.$\mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - 3x + 4}}{{x - 2}}$.
C.$\mathop {\lim }\limits_{x \to {2^ + }} \frac{{ - 3x + 4}}{{x - 2}}$.
D.$\mathop {\lim }\limits_{x \to - \infty } \frac{{ - 3x + 4}}{{x - 2}}$.
Cho hàm số $y = f\left( x \right)$ liên tục trên $\left( {a;b} \right)$. Điều kiện cần và đủ để hàm số liên tục trên $\left[ {a;b} \right]$ là
A.$\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right)$và $\mathop {\lim }\limits_{x \to {b^ + }} f\left( x \right) = f\left( b \right)$.
B.$\mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = f\left( a \right)$và $\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)$.
C.$\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right)$và $\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)$.
D.$\mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = f\left( a \right)$và $\mathop {\lim }\limits_{x \to {b^ + }} f\left( x \right) = f\left( b \right)$.
Cho hàm số $y = \frac{{x - 3}}{{{x^2} - 1}}$. Mệnh đề nào sau đây đúng?
A. Hàm số không liên tục tại các điểm $x = \pm 1$.
B. Hàm số liên tục tại mọi $x \in \mathbb{R}$.
C. Hàm số liên tục tại điểm $x = - 1$.
D. Hàm số liên tục tại điểm $x = 1$.
Tìm $m$ để hàm số \[f(x) = \left\{ \begin{gathered}
\frac{{{x^2} - 4}}{{x + 2}}\quad \,{\text{khi}}\;x \ne - 2 \hfill \\
\quad m\quad \quad {\text{khi}}\;x = - 2 \hfill \\
\end{gathered} \right.\] liên tục tại $x = - 2$.
A.$m = - 4$.
B.$m = 2$.
C.$m = 4$.
D.$m = 0$.
Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là
A. 5 mặt, 5 cạnh.
B. 6 mặt, 5 cạnh.
C. 6 mặt, 10 cạnh.
D. 5 mặt, 10 cạnh.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
B. Hai đường thẳng chéo nhau khi chúng không có điểm chung.
C. Hai đường thẳng song song khi chúng ở trên cùng một mặt phẳng.
D. Khi hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
Cho hình hộp $ABCD.EFGH$. Mệnh đề nào sau đây sai?
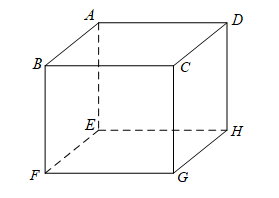
A. $BG$ và $HD$ chéo nhau.
B. $BF$ và $AD$ chéo nhau.
C. $AB$ song song với $HG$.
D. $CG$ cắt $HE$.
Cho hình chóp $S.ABCD$ có đáy$ABCD$ là hình bình hành tâm $O$. Gọi $I,J$ lần lượt là trung điểm của $SA$ và $SC$. Đường thẳng \[IJ\] song song với đường thẳng nào?
A.$BC$.
B. $AC$.
C.$SO$.
D.$BD$.
Cho các giả thiết sau đây. Giả thiết nào kết luận đường thẳng $a$ song song với mặt phẳng $\left( \alpha \right)$.
A.$a{\text{//}}b$ và $b \subset \left( \alpha \right)$.
B. $a{\text{//}}\left( \beta \right)$ và $\left( \beta \right){\text{//}}\left( \alpha \right)$.
C.$a{\text{//}}b$ và $b{\text{//}}\left( \alpha \right)$.
D.$a \cap \left( \alpha \right) = \emptyset $.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AB$. Gọi $P,Q$ lần lượt là hai điểm nằm trên cạnh $SA$và $SB$ sao cho $\frac{{SP}}{{SA}} = \frac{{SQ}}{{SB}} = \frac{1}{3}$. Khẳng định nào sau đây là đúng?
A.$PQ$ cắt $\left( {ABCD} \right)$.
B. $PQ \subset \left( {ABCD} \right)$.
C.$PQ{\text{//}}\left( {ABCD} \right)$ .
D.$PQ$ và $CD$ chéo nhau.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$, $M$ là trung điểm của $SA$. Khẳng định nào sau đây là đúng?
A.$OM{\text{//}}\left( {SCD} \right)$.
B. $OM{\text{//}}\left( {SBD} \right)$.
C.$OM{\text{//}}\left( {SAB} \right)$ .
D.$OM{\text{//}}\left( {SAD} \right)$.
Cho hai mặt phẳng phân biệt $\left( P \right)$ và $\left( Q \right)$, đường thẳng $a \subset \left( P \right)$; $b \subset \left( Q \right)$. Tìm khẳng định sai trong các mệnh đề sau.
A. Nếu $\left( P \right){\text{//}}\left( Q \right)$ thì $a{\text{//}}b$.
B. Nếu $\left( P \right){\text{//}}\left( Q \right)$ thì $b{\text{//}}\left( P \right)$.
C. Nếu $\left( P \right){\text{//}}\left( Q \right)$ thì $a$ và $b$ hoặc song song hoặc chéo nhau .
D. Nếu $\left( P \right){\text{//}}\left( Q \right)$ thì $a{\text{//}}\left( Q \right)$.
Có bao nhiêu mặt phẳng song song với cả hai đường thẳng chéo nhau?
A. Vô số.
B.\[3\].
C.$2$.
D.$1$.
Cho hình lăng trụ $ABCD.A'B'C'D'$. Tìm mệnh đề sai trong các mệnh đề sau
A.$\left( {AA'B'B} \right)$song song với $\left( {CC'D'D} \right)$.
B. Diện tích hai mặt bên bất kì bằng nhau.
C.\[AA'\] song song với \[CC'\].
D. Hai mặt phẳng đáy song song với nhau.
Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình bình hành tâm $O$. Gọi $M,N$ lần lượt là trung điểm $SA,SD$. Mặt phẳng $\left( {OMN} \right)$ song song với mặt phẳng nào sau đây?
A.$\left( {SBC} \right)$.
B.$\left( {SCD} \right)$.
C.$\left( {ABCD} \right)$.
D.$\left( {SAB} \right)$.
Qua phép chiếu song song, tính chất nào không được bảo toàn?
A. Chéo nhau.
B. Đồng qui.
C. Song song.
D. Thẳng hàng.
Điều tra về chiều cao của học sinh khối lớp 11 của trường, ta được mẫu số liệu sau:
|
Chiều cao (cm) |
Số học sinh |
|
$\left[ {150;152} \right)$ |
10 |
|
$\left[ {152;154} \right)$ |
18 |
|
$\left[ {154;156} \right)$ |
38 |
|
$\left[ {156;158} \right)$ |
26 |
|
$\left[ {158;160} \right)$ |
15 |
|
$\left[ {160;162} \right)$ |
7 |
Mẫu số liệu ghép nhóm đã cho có bao nhiêu nhóm?
A. 5.
B. 6.
C. 7.
D. 12.
Mẫu số liệu sau cho biết cân nặng của học sinh lớp 11 trong một lớp
|
Cân nặng (kg) |
Dưới 55 |
Từ 55 đến 65 |
Trên 65 |
|
Số học sinh |
23 |
15 |
2 |
Số học sinh của lớp đó là bao nhiêu?
A. 40.
B. 35.
C. 23.
D. 38.
Kết quả khảo sát cân nặng của 25 quả cam ở lô hàng A được cho ở bảng sau:
|
Cân nặng (g) |
$\left[ {150;155} \right)$ |
$\left[ {155;160} \right)$ |
$\left[ {160;165} \right)$ |
$\left[ {165;170} \right)$ |
$\left[ {170;175} \right)$ |
|
Số quả cam lô hàng A |
3 |
1 |
6 |
11 |
4 |
Nhóm chứa mốt là nhóm nào?
A. $\left[ {150;155} \right)$.
B. $\left[ {155;160} \right)$.
C. $\left[ {165;170} \right)$.
D. $\left[ {170;175} \right)$.
Người ta tiến hành phỏng vấn 40 người về một mẫu áo khoác. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm là $100.$ Kết quả được trình bày trong bảng ghép nhóm sau:
|
Nhóm |
$\left[ {50;60} \right)$ |
$\left[ {60;70} \right)$ |
$\left[ {70;80} \right)$ |
$\left[ {80;90} \right)$ |
$\left[ {90;100} \right)$ |
|
|
Tần số |
$4$ |
$5$ |
$23$ |
$6$ |
$2$ |
$N = 40$ |
Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị
A. $74$.
B. \[75.\]
C. \[76.\]
D. \[77.\]
Để chuẩn bị cho đồ án tốt nghiệp, một sinh viên y khoa đã khảo sát huyết áp tối đa của một số bệnh nhân và lập được bảng tần số ghép nhóm sau:
|
Huyết áp |
Tần số |
|
$\left[ {90;110} \right)$ |
6 |
|
$\left[ {110;130} \right)$ |
20 |
|
$\left[ {130;150} \right)$ |
35 |
|
$\left[ {150;170} \right)$ |
45 |
|
$\left[ {170;190} \right)$ |
30 |
|
$\left[ {190;210} \right)$ |
16 |
Tìm tứ phân vị thứ ba của mẫu số liệu trên.
A. $155,9$.
B. \[136,9.\]
C. \[156,7.\]
D. \[175,3.\]

